
🎬 个人主页 :MSTcheng · CSDN
🌱 代码仓库 :MSTcheng · Gitee
🔥 精选专栏 : 《C语言》
《数据结构》
《算法学习》
《C++由浅入深》
💬座右铭: 路虽远行则将至,事虽难做则必成!
上期我们给大家介绍了朴素的二分模板,本期我们就进入二分的进阶,从原来的查找一个数,进阶到查找两个数,且这两个数是一个区间的左右边界。
我们先来看题:
一、34. 在排序数组中查找元素的第一个和最后一个位置
1.1题目解析

1.2算法原理
1、暴力解法: 就是去遍历一遍原数组,而且还要人为去判断边界情况,返回第一个出现target值位置的下标,和最后一个出现target值位置的下标,时间肯定是O(N)。会超时这里就不展示了。
2、二分查找:
1、查找区间的左端点:
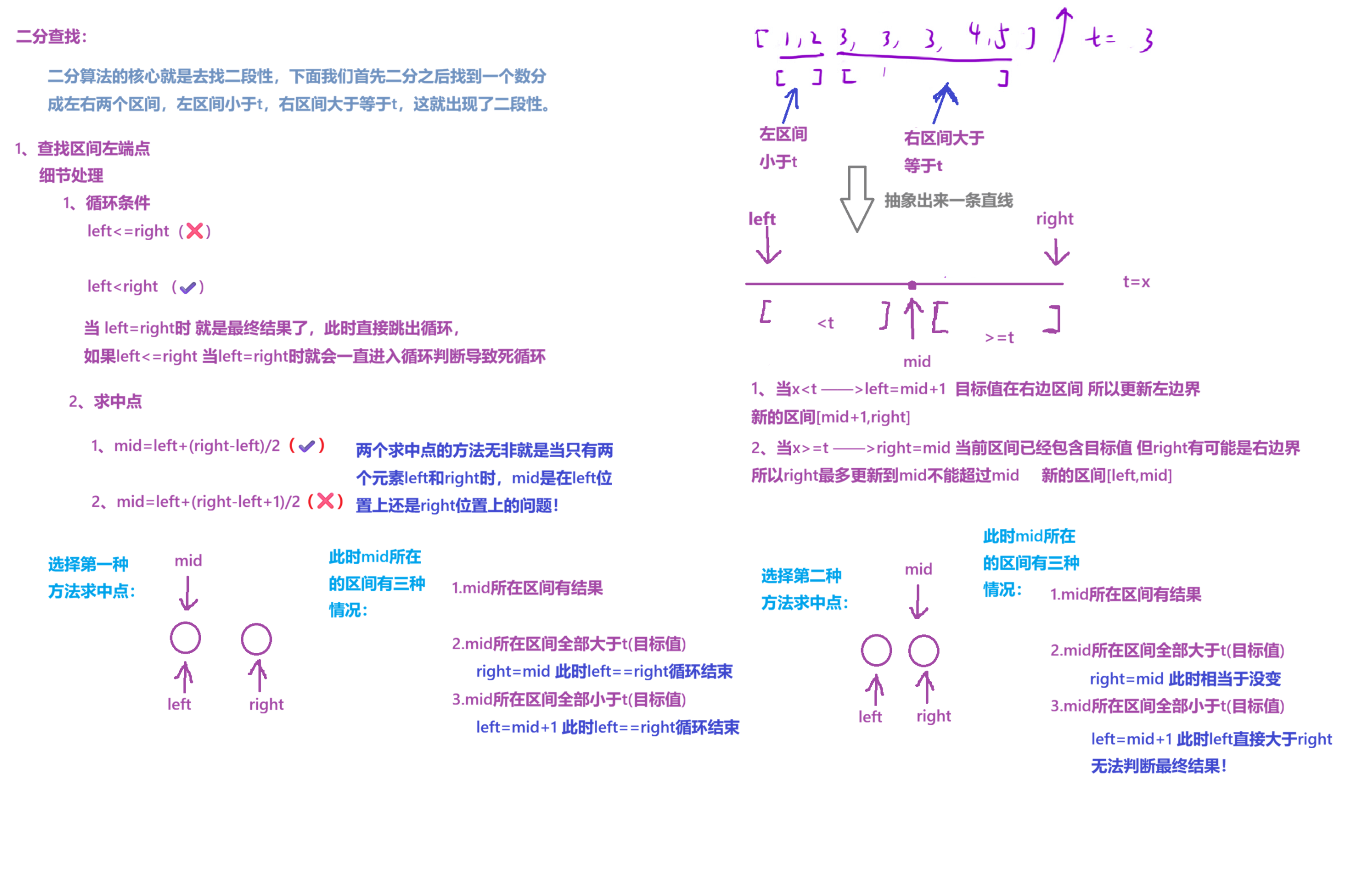
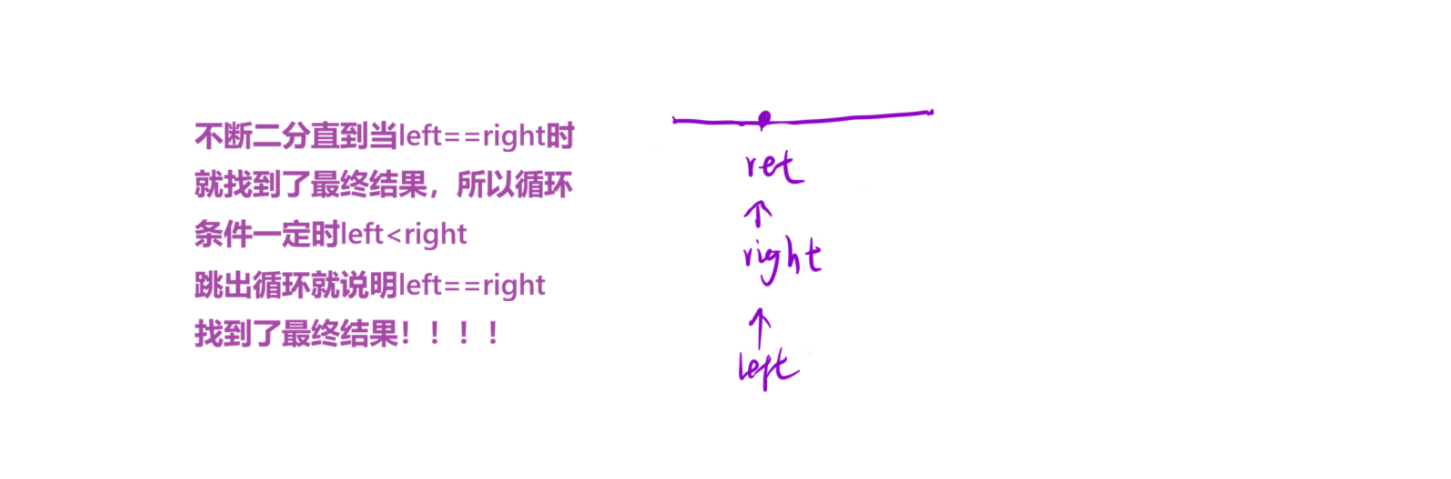
以上是本题查找区间左端点的算法,以题目的示例1为例,示例1让我们找到数组中等于
target值的初始位置和结束位置:也就是下标3和下标4。上面的算法就是在查找下标3! 下面我们再来看看查找区间右端点,也就是查找4!
2、查找区间右端点:

查找右端点判断逻辑说明:
1、当
x<=t时 此时目标值在左区间 所以不断二分缩小左区间直到找到最终结果left=mid注意left不能超过mid因为某一次的mid所对应的值可能就是右端点。
2、当x>t时 说明mid右区间一定不含目标值 ,所以直接大胆将right=mid-1,将right直接更新到mid-1,因为mid处的值已经大于目标值了,而mid-1的值不确定,所以将right更新到mid-1处 再继续二分。 一定能分到x<=t的那一个区间,等mid处于那一个区间了以后就按照第一步,不断缩小左区间即可!
1.3代码编写
cpp
class Solution
{
public:
vector<int> searchRange(vector<int>& nums, int target)
{
//定义两个指针
int left=0,right=nums.size()-1;
vector<int> ret;
int begin=0;
//处理特殊情况
if(nums.size()==0)
{
return ret={-1,-1};
}
//二分查找
while(left<right)
{
//细节二 一定是(right-left)/2 这样mid算的才是偏左的点
int mid=left+(right-left)/2;
if(nums[mid]<target)
{
//使用mid 分成左右两个区间 左区间的值都小于target 右区间的值都大于或等于target
//更新左区间
left=mid+ 1;
}
else //(nums[mid]>=target)
{
//此时区间里面包含目标值 缩小右指针
right=mid;
}
}
//跳出循环 left==right 此时已经得到结果了
if(nums[left]!=target)
{
return ret={-1,-1};
}
begin=left;//标记一下左端点
//⼆分右端点
//这里一定要重新计算 因为上面的right已经发生变化了
left = 0, right = nums.size() - 1;
while(left < right)
{
//注意 查找右端点求中点要加一
int mid = left + (right - left + 1) / 2;
if(nums[mid] <= target)
{
left = mid;
}
else
{
right = mid - 1;
}
}
return {begin, right};
//查找右边界
//法二:也可以根据左边界 增加一个计数器去计算该区间target值的个数
//最后使用左端点加上个数就等于右端点的下标了
// int i=0;
// auto it=nums.begin()+left;
// while(it!=nums.end())
// {
// if(*it==nums[left])
// {
// i++;
// }
// it++;
// }
// return ret={left,right+i-1};
}
};二、35. 搜索插入位置
2.1题目解析

2.2算法原理

2.3代码编写
cpp
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left=0,right=nums.size()-1;
int mid=0;
while(left<= right)
{
// 计算中间索引,避免 left + right 溢出(C++ 中整数溢出会导致未定义行为,此写法为最佳实践)!!!
mid=left+(right-left)/2;
if(nums[mid]<target)
{
//往右边去查找
left=mid+1;
}
else if(nums[mid]>target)
{
//往左边去查找
right=mid-1;
}
else
{
//找到了就直接返回该下标
return mid;
}
}
//没找到按顺序返回插入的位置 此时left被更新成了left+1
return left;
}
};三、69. x 的平方根
3.1题目解析

3.2算法原理
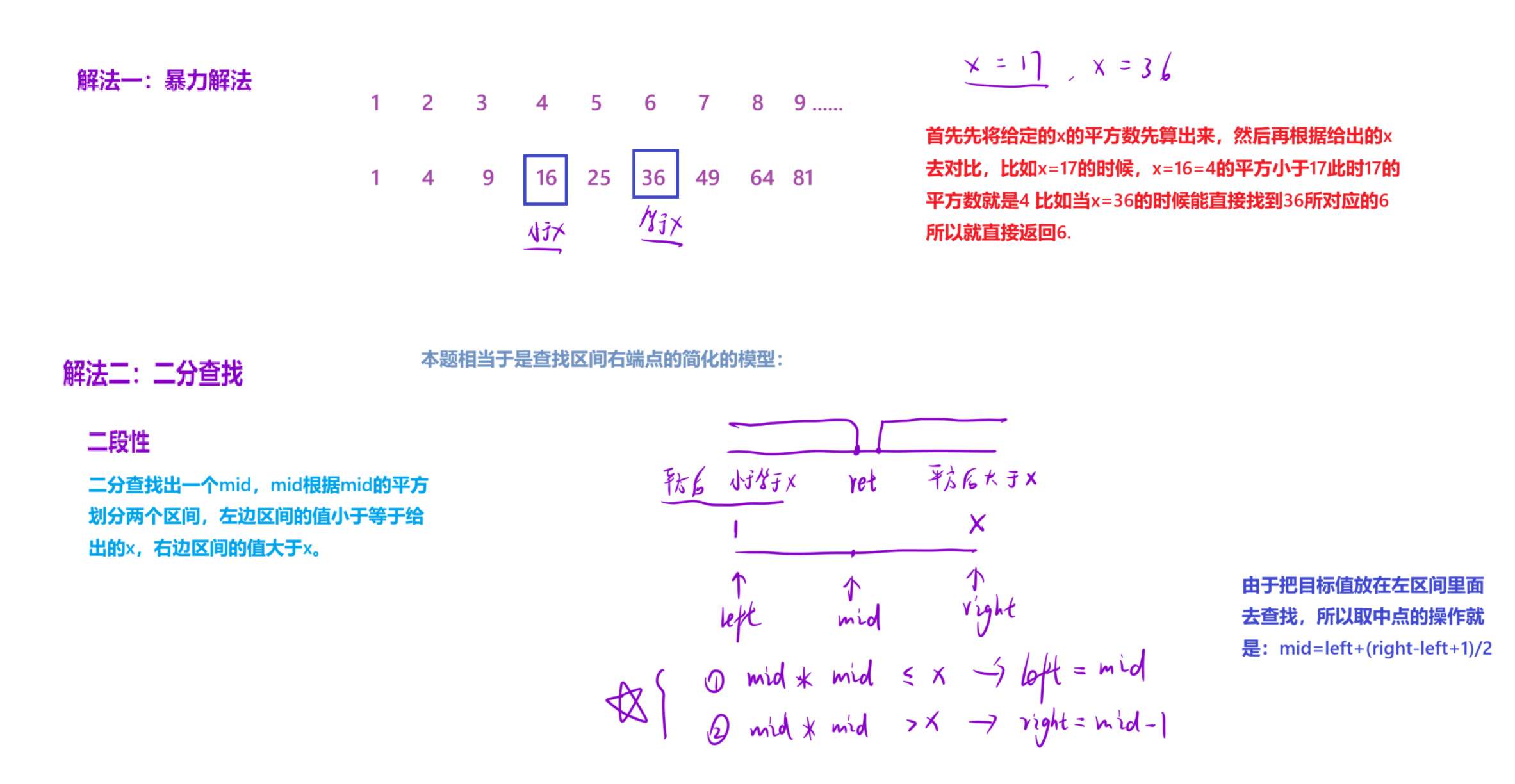
3.3编写代码
cpp
class Solution {
public:
int mySqrt(int x) {
//处理一下特殊情况
if(x<=1)
{
return x;
}
//使用二分 right最多到x,因为给出的x一定在0------x^2中
long left=1,right=x;
long mid=0;
while(left<right)
{
//使用偏右的中间值求法
mid=left+(right+1-left)/2;
if(mid*mid<=x)
{
//更新左区间
left=mid;
}
else
{
//更新右区间
right=mid-1;
}
}
return (int)left;
}
};四、852. 山脉数组的峰顶索引
4.1题目解析
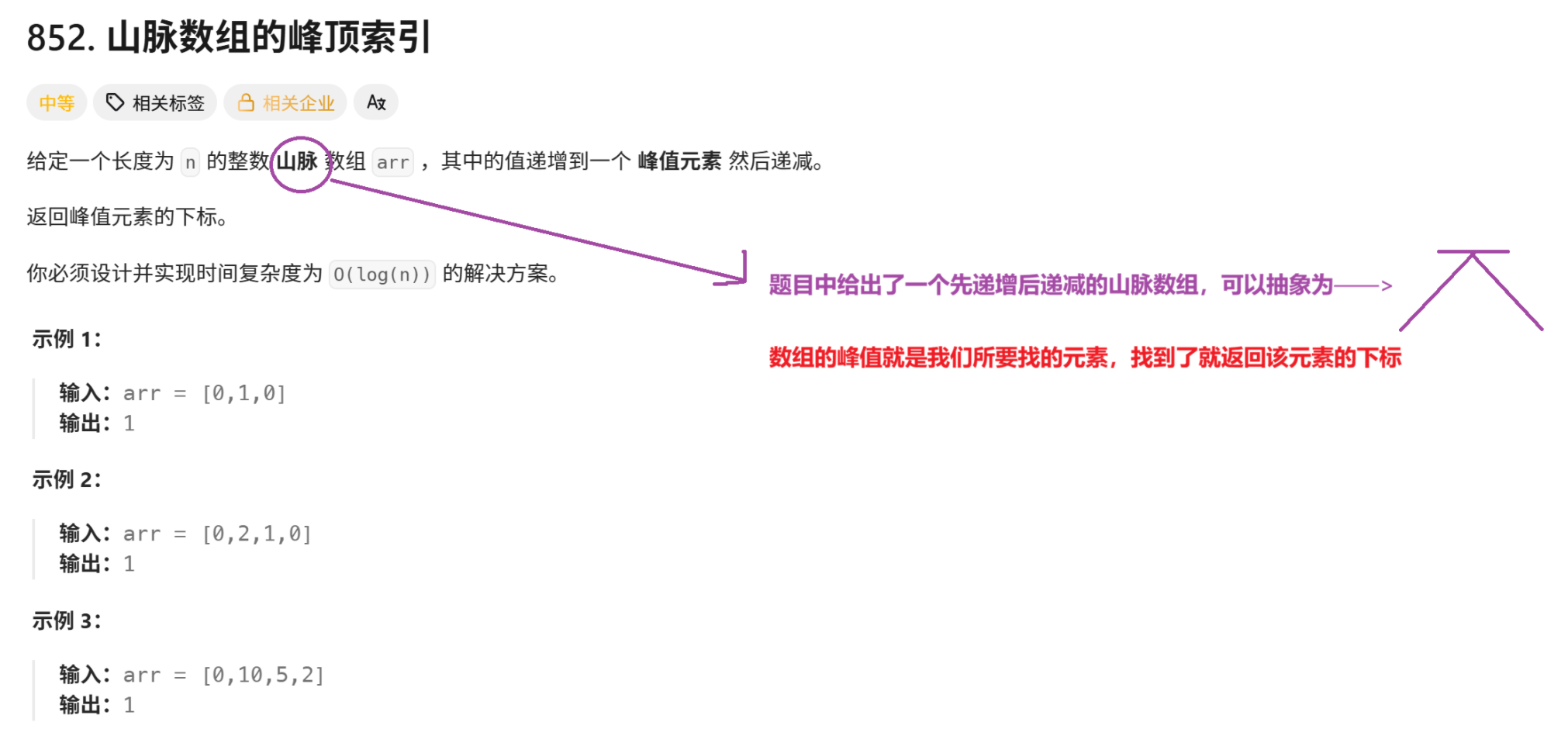
4.2算法原理
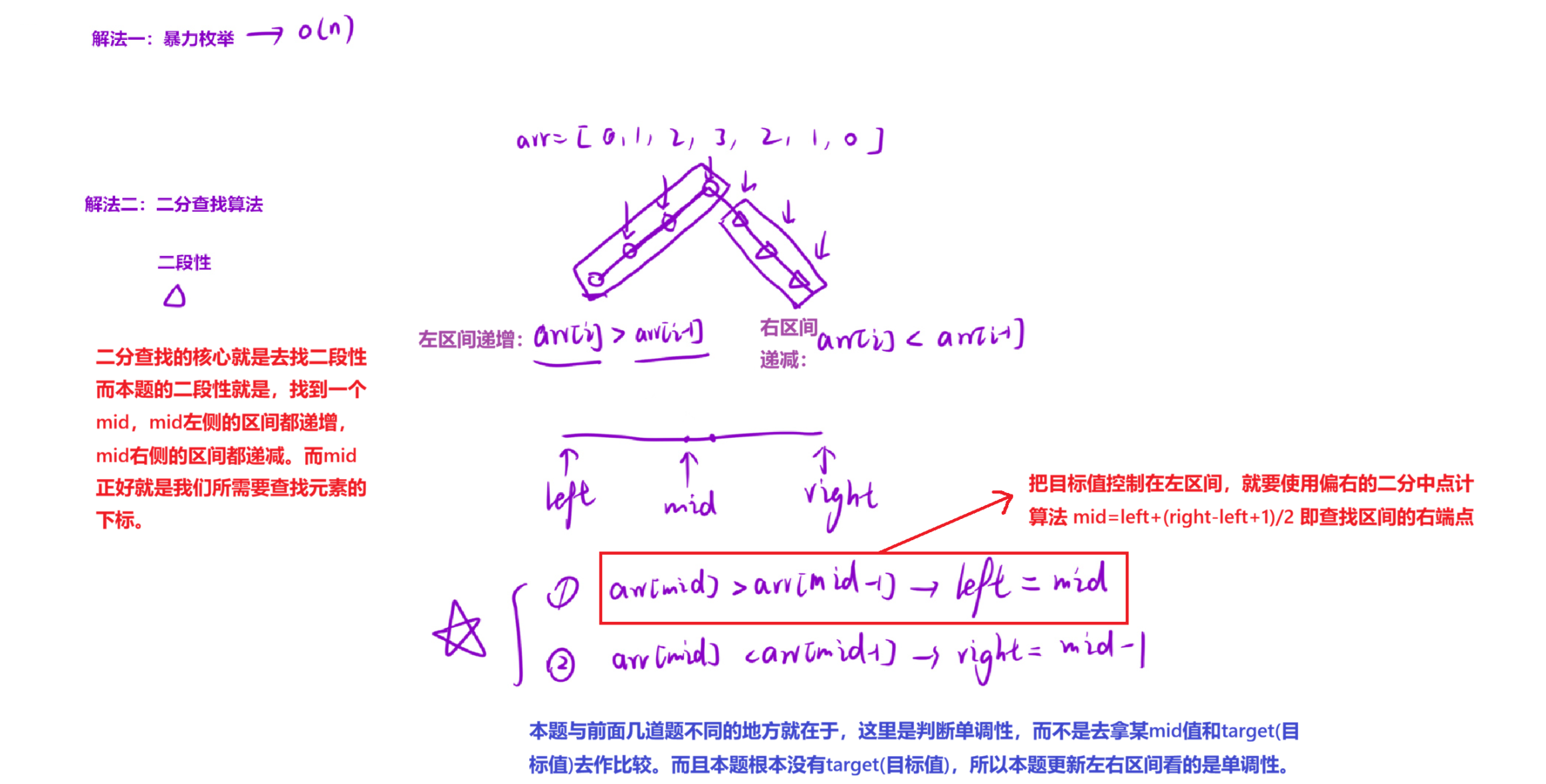
注意:
arr[mid]>arr[mid-1] ->left=mid是将目标值放在左区间,然后不断缩小左区间直至left==right,就找到了最终的目标值。
arr[mid]<arr[mid-1] ->right=mid-1当所计算的mid值在右边递减的区间时,因为我们要把目标值放在左区间,所以递减区间一定不含有目标值,直接大胆的将right更新到mid-1的位置 ,直到缩小到左区间,然后就按照上面的逻辑继续执行直到找到结果为止!!!
4.3编写代码
cpp
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int left=0,right=arr.size();
while(left<right)
{
//使用偏右的二分
int mid=left+(right-left+1)/2;
if(arr[mid]>arr[mid-1])
{
//更新左区间
left=mid;
}
if(arr[mid]<arr[mid-1])
{
//此时要往左区间里面去查找
//更新右区间
right=mid-1;
}
}
return left;
}
};五、总结
1、二分算法的核心:
就是去找一个二段性 ,能够找到一个
mid对于的值,mid左边的区间都小于它,mid右边的区间都大于它。或者mid左边的区间都是单调递增,mid右边的区间都是单调递减。以及其他的二段性...
2、求中点的计算方法:
如果是把目标值放在左边区间,那么就使用求区间右端点的查找逻辑,如果是把目标值放在右边区间,那么就使用求区间左端点的查找逻辑。以第一题为模板,后面几题全都是第一题的变形,都是使用计算区间左右端点的查找逻辑。