基于最小二乘拟合减小四轮定位数据采集误差的方法

一、问题的提出：

问题是这样的，在四轮定位中，方向盘在不断左右转动的情况，要快速获取转向角10°点对应外倾角数据来计算四轮定位的相关参数。由于车身存在发动机的振动，导致传感器数据会存在一定的跳动，在采集10°转向角的数据点时，实时采集到的传感器数据不那么准确，会有一个小幅度的波动。

那么如何才能采集准确呢？

考虑到小角度范围内，轮胎转向角和轮胎外倾角之间可能是线性关系。这样我们就可以实时采集7°到10°的多个点的外倾角数据，然后使用最小二乘拟合法来精准计算10°点时的外倾角。

下图是手测的一组数据，左侧为轮胎转向角，右侧为外倾角。

将上图生成二维图，如下：

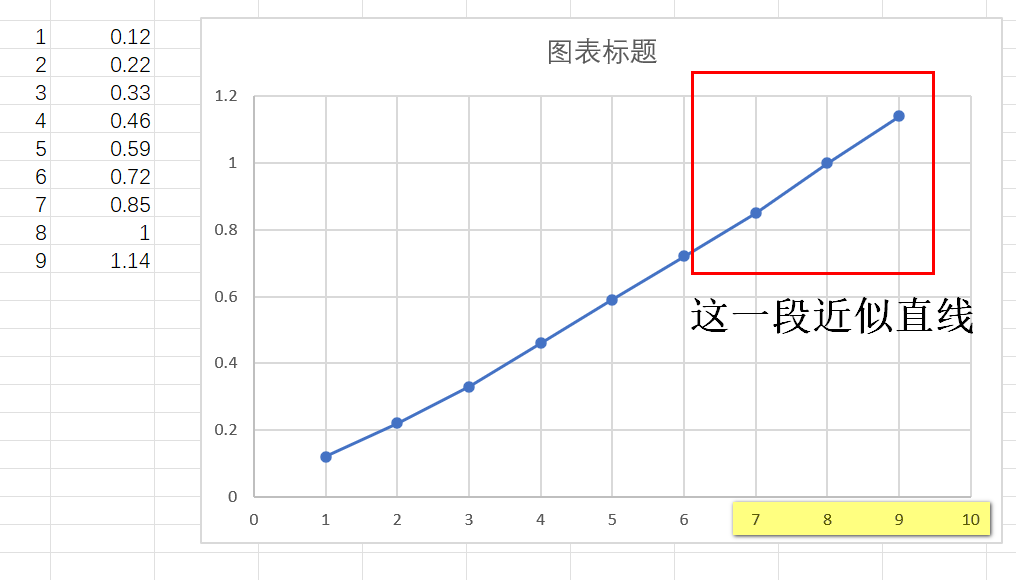
可以看到，确实是近似直线。

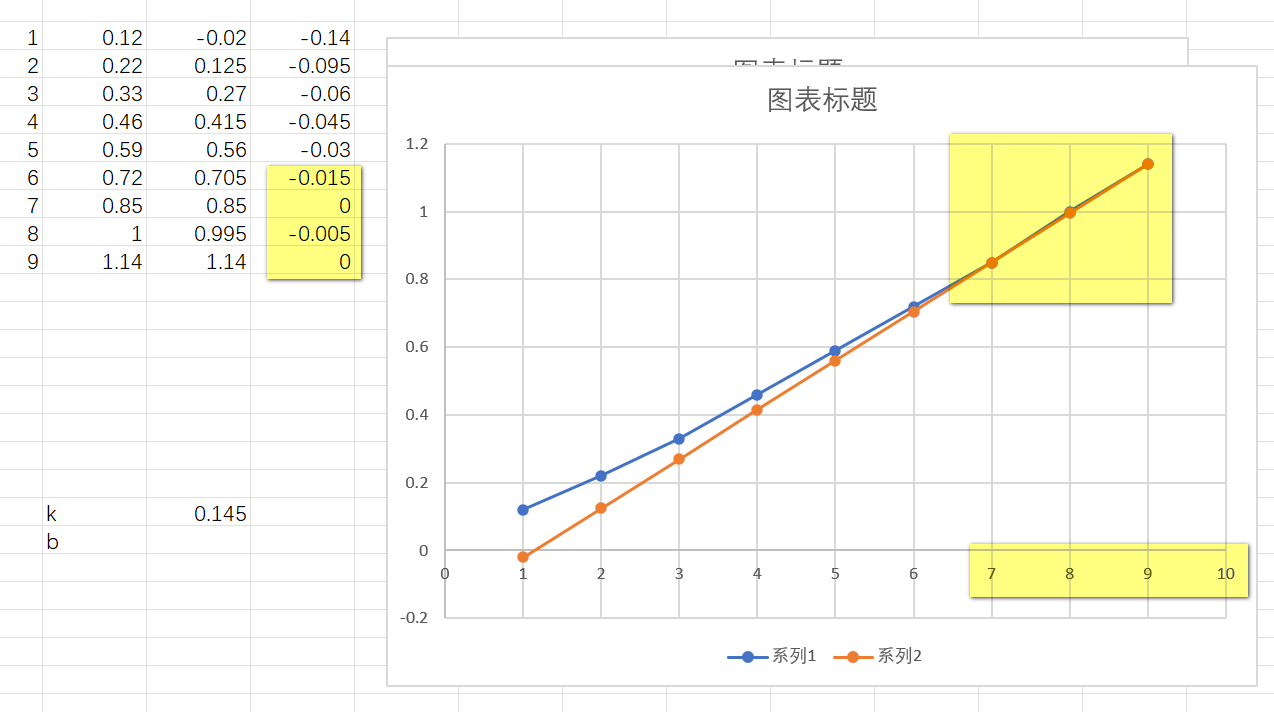
即使做一个简单的直线拟合，也可以看到7-9°之间的误差只有0.005°。这说明这个思路是完全可行。

二、解决方法：

下面就开始正式进行讲解解决方案。

基于轮胎转向角和外倾角的采样数据，实现线性最小二乘法拟合，根据拟合出的直线方程，计算任意转向角对应的外倾角（比如 10°），并最小化传感器噪声带来的误差。

1、算法原理

线性拟合的核心是求直线方程 y = k*x + b（x = 转向角，y = 外倾角）：

斜率 k = (n*Σxy - Σx*Σy) / (n*Σx² - (Σx)²)
截距 b = (Σy - k*Σx) / n其中：
n 是数据点数量
Σx 是所有转向角的和，Σy 是所有外倾角的和
Σxy 是每个 x*y 的和，Σx² 是每个 x² 的和

2、完整 C 函数实现

现在给出函数，该函数无依赖，可直接放入 STM32 工程，支持任意数量的采样点：

cpp 复制代码

#include <stdint.h>
#include <math.h>  // 数学计算

/**
 * @brief  线性最小二乘法拟合（y = k*x + b）
 * @param  data: 二维数组，格式为[data[0][0]=转向角1, data[0][1]=外倾角1, 
                                data[1][0]=转向角2, data[1][1]=外倾角2,...]
 * @param  data_num: 数据点数量（比如你的示例是9个点，填9）
 * @param  k: 输出参数，拟合直线的斜率
 * @param  b: 输出参数，拟合直线的截距
 * @retval 0: 成功，-1: 输入参数错误（避免除零）
 */
int32_t linear_least_square_fit(const float data[][2], uint8_t data_num, 
float *k, float *b)
{
    // 入参合法性检查
    if (data == NULL || k == NULL || b == NULL || data_num < 2)
    {
        return -1;  // 至少需要2个点才能拟合直线
    }

    // 初始化求和变量
    float sum_x = 0.0f;   // Σx
    float sum_y = 0.0f;   // Σy
    float sum_xy = 0.0f;  // Σxy
    float sum_x2 = 0.0f;  // Σx²

    // 遍历所有数据点，计算各项求和值
    for (uint8_t i = 0; i < data_num; i++)
    {
        sum_x += data[i][0];
        sum_y += data[i][1];
        sum_xy += data[i][0] * data[i][1];
        sum_x2 += data[i][0] * data[i][0];
    }

    // 计算分母（避免除零）
    float denominator = data_num * sum_x2 - sum_x * sum_x;
    if (fabs(denominator) < 1e-6)  // 分母接近0，说明所有x值相同，无法拟合
    {
        return -1;
    }

    // 计算斜率k和截距b
    *k = (data_num * sum_xy - sum_x * sum_y) / denominator;
    *b = (sum_y - *k * sum_x) / data_num;

    return 0;
}

/**
 * @brief  根据拟合的直线方程，计算任意转向角对应的外倾角
 * @param  angle: 输入的转向角（比如10°）
 * @param  k: 拟合得到的斜率
 * @param  b: 拟合得到的截距
 * @retval 对应的外倾角
 */
float calculate_camber_angle(float angle, float k, float b)
{
    return k * angle + b;
}

// ========== 测试示例 ==========
int main(void)
{
    // 采样数据：[转向角, 外倾角]
    // 根据实际情况来，如果采集了30个数据，相应代码稍作修改。
    // 如果采集10°转向点，那么请仅只采集10°附近的点，比如从7°开始到10°。
    // 下面的示例是从1°开始的，请尽量不要这么做，因为角度越远误差越大。
    float camber_data[9][2] = {
        {1.0f, 0.12f},
        {2.0f, 0.22f},
        {3.0f, 0.33f},
        {4.0f, 0.46f},
        {5.0f, 0.59f},
        {6.0f, 0.72f},
        {7.0f, 0.85f},
        {8.0f, 1.00f},
        {9.0f, 1.14f}
    };

    float k_fit = 0.0f;  // 拟合斜率
    float b_fit = 0.0f;  // 拟合截距

    // 执行线性拟合
    if (linear_least_square_fit(camber_data, 9, &k_fit, &b_fit) == 0)
    {
        // 输出拟合结果（可通过串口打印到上位机）
        // 示例：k≈0.1267，b≈-0.0178（基于你的数据计算）
        // printf("拟合直线：y = %.4f*x + %.4f\r\n", k_fit, b_fit);

        // 计算10°转向角对应的外倾角
        float camber_10 = calculate_camber_angle(10.0f, k_fit, b_fit);
        // printf("10°转向角对应的外倾角：%.4f\r\n", camber_10);  // 约1.249°
    }
    else
    {
        // 拟合失败处理（比如串口打印错误）
        // printf("线性拟合失败！\r\n");
    }

    while (1)
    {
        // TODO:
        // 其他代码... ...
    }
}

上面就讲完了。

3、误差验证

如果需要验证拟合误差，可使用以下函数，计算每个采样点的拟合值与实际值的均方误差（MSE），越小说明拟合效果越好：

cpp 复制代码

/**
 * @brief  计算拟合的均方误差（验证拟合效果）
 * @param  data: 原始数据
 * @param  data_num: 数据点数量
 * @param  k: 拟合斜率
 * @param  b: 拟合截距
 * @retval 均方误差（越小越好）
 */
float calculate_mse(const float data[][2], uint8_t data_num, float k, float b)
{
    float mse = 0.0f;
    for (uint8_t i = 0; i < data_num; i++)
    {
        float y_fit = k * data[i][0] + b;
        mse += (y_fit - data[i][1]) * (y_fit - data[i][1]);
    }
    return mse / data_num;
}

以上，就是全部！

这篇文章，也可以应用其他需要线性拟合的领域，特别是传感器数据处理领域，包括求解与衡量均方根误差。