114. 二叉树展开为链表

中等

提示

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树先序遍历顺序相同。

示例 1：

复制代码

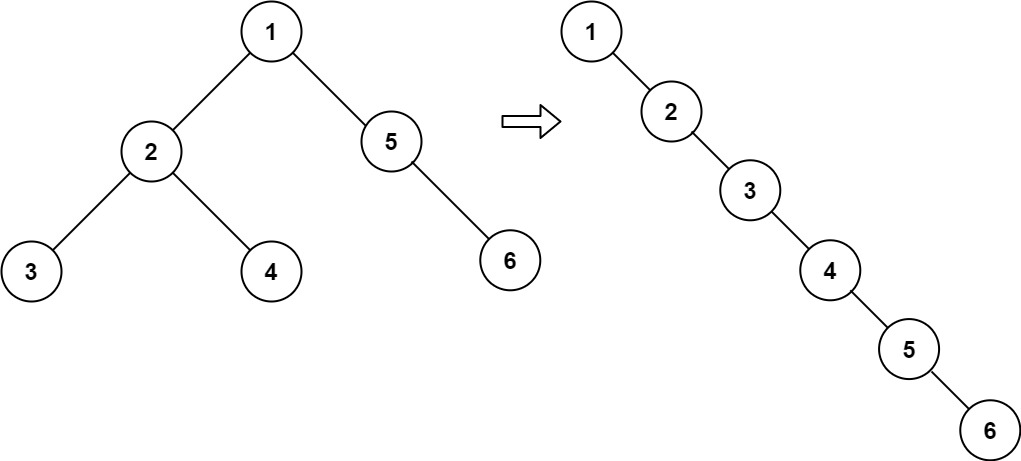
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

复制代码

输入：root = []
输出：[]

示例 3：

复制代码

输入：root = [0]
输出：[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

📝 核心笔记：二叉树展开为链表 (Flatten Binary Tree to Linked List)

1. 核心思想 (一句话总结)

"倒着织毛衣：既然要求结果是 1->2->3->4**，那我就先找到 4，再把 3 接在 4 前面，再把 2 接在 3 前面......"**

目标顺序：前序遍历 (Root -> Left -> Right)。
构建顺序 ：Right -> Left -> Root (逆后序)。
技巧：维护一个全局变量 head，它永远指向当前已经拉直的链表的头节点 。当前节点 root 只需要把自己连到 head 上，然后自己成为新的 head。

2. 算法流程 (递归三步曲)

递归右子树：先去处理最右边的节点（因为那是链表的尾巴）。
递归左子树：处理左边的节点。
当前节点操作 (Wiring)：

- root.right = head：我的右手指着刚才处理完的那一串链表的头。
- root.left = null：左手必须断开（题目要求）。
- head = root：我也加入链表了，现在我是排头兵，下一个处理的人（我的父节点）要连我。

🔍 代码回忆清单

复制代码

// 题目：LC 114. Flatten Binary Tree to Linked List
class Solution {
    // 全局变量：记录"已经拉直的链表"的头节点
    // 初始为 null，表示链表末尾的 next 是 null
    private TreeNode head = null;

    public void flatten(TreeNode root) {
        // 1. Base Case
        if (root == null) {
            return;
        }

        // 2. 核心遍历顺序：右 -> 左 -> 根
        // 这与前序遍历 (根->左->右) 正好相反
        flatten(root.right);
        flatten(root.left);
        
        // 3. 链表拼接 (头插法)
        // 此时 head 指向的是右边已经处理好的一长串
        // 比如对于根节点 1，处理完左右后，head 指向 2 (2->3->4->5->6)
        
        root.right = head; // 1 -> 2
        root.left = null;  // 断开左边
        
        head = root; // 更新 head 为 1，供上一层使用
    }
}

⚡ 快速复习 CheckList (易错点 & 寻找前驱解法)

为什么是先右后左？

- 如果先左后右，处理完左边后，head 指向左子树的头。此时再处理根节点，把根连向左子树，那右子树就丢了（或者接不上了）。
- 逆向顺序保证了我们总是从链表的 Tail 往 Head 建。

面试进阶： $O(1)$ 空间解法 (寻找前驱节点)？

- 虽然您的递归解法空间是 $O(N)$ (栈)，但代码最简洁。
- 面试官可能问："如果不允许用递归栈，纯 $O(1)$ 空间怎么做？"
- 思路 (Morris 遍历变体)：

1. 1. 找到当前节点左子树的 最右节点 (前驱)。
  2. 把当前节点的 右子树 嫁接到这个 最右节点 的右边。
  3. 把左子树移到右边，左边置空。
  4. 继续处理下一个右节点。

🖼️ 数字演练

树：

复制代码

目标：1->2->3->4->5->6

Flatten(6) : head=6.
Flatten(5):

- Right(6) done. head=6.
- Left(null).
- 5.right=6, head=5. (链表: 5->6)

Flatten(4) : head=4. (链表: 4) 注：4是叶子，前面的 5->6 是在另一侧递归栈里
Flatten(3) : head=3.
Flatten(2):

- Right(4) done. head=4. (链表: 4)
- Left(3) done. head=3. (链表: 3->4)
- 2.right=3. head=2. (链表: 2->3->4)
- 注意：此时 2 的右子树其实是 4，但在递归过程中我们用 head 串起来了。

Flatten(1):

- Right(5) done. head=5. (链表: 5->6)
- Left(2) done. head=2. (链表: 2->3->4... 此时 4.right 其实在上一层递归还没连上 5？不对，逻辑是全局 head)
- 修正逻辑：

- - 递归到 5 时，head 是 6。5->6, head=5.
  - 递归到 4 时，head 是 5。4->5, head=4.
  - 递归到 3 时，head 是 4。3->4, head=3.
  - 递归到 2 时，head 是 3。2->3, head=2.
  - 递归到 1 时，head 是 2。1->2, head=1.

- 最终 : 1->2->3->4->5->6.