【算法提高篇】（二）线段树之区间修改：懒标记的核心奥义与实战实现

前言

在算法竞赛和数据结构实战中，线段树是处理区间问题的 "万金油"，单点修改、区间查询的基础线段树能解决不少问题，但面对区间整体修改的场景时，基础版本的时间复杂度会直接退化到 O (n)，在 n 和操作次数都达到 10^5 的量级时会直接超时。而懒标记（Lazy Tag）的出现，让线段树的区间修改操作依然能保持 O (logn) 的时间复杂度，成为线段树进阶的核心知识点。本文将从问题痛点出发，一步步拆解懒标记的设计思想，手把手实现带懒标记的线段树区间修改 + 区间查询，让你彻底吃透这个核心技巧。下面就让我们正式开始吧！

一、为什么基础线段树处理区间修改会 "拉胯"？

在讲懒标记之前，我们先回顾下基础线段树的单点修改逻辑：递归找到目标叶子节点，修改后一路向上pushup更新父节点的信息，整个过程只涉及从根到叶子的一条路径，时间复杂度 O (logn)。

但如果要对**[l,r] 区间内的所有元素加 k**，比如对数组 [5,1,3,0,2,2,7,4,5,8] 的 [4,9] 区间每个元素加 2，用基础线段树该怎么做？只能遍历区间内的每一个位置，逐个执行单点修改。如果区间是 [1,10^5]，这个操作就需要执行 10^5 次，每次 O (logn)，整体时间复杂度直接飙升到 O (nlogn)，面对 10^5 次这样的操作，程序必然超时。

核心痛点在于：基础线段树无法对 "整段区间的统一修改" 做批量处理，只能逐点修改。那有没有办法让线段树识别出 "整段区间被完全覆盖" 的情况，直接对这个区间的节点做批量修改，而不深入到叶子节点？这就是懒标记的核心思路。

二、懒标记的核心设计思想："延迟更新，按需下发"

懒标记的本质是一种延迟更新的策略 ，核心可以用八个字概括：延迟更新，按需下发。我们先理解这个思想的核心逻辑，再看具体的实现。

2.1 核心思路拆解

线段树的每个节点都维护着一段区间的信息（比如区间和），当我们对某个节点的整个区间执行统一修改时（比如全区间加 k），我们可以做两件事：

立即更新当前节点的维护信息 ：比如区间和，直接用区间和 += 区间长度 * k计算出新的区间和，一步到位；

打上懒标记 ：在节点中额外维护一个标记（比如add），记录这个区间的所有元素需要加 k，但暂时不把这个修改下发到它的左右孩子节点。

这样做的好处是，一次区间修改如果能覆盖某个节点的整段区间，只需要 O (1) 的时间修改当前节点和打标记，无需递归到叶子，效率直接拉满。

而 "懒" 的体现就在延迟更新 ：这个标记会一直保存在当前节点，直到后续的修改或查询操作需要访问该节点的孩子节点时 ，才把懒标记的内容 **下发（pushdown）**给左右孩子，更新孩子的信息并给孩子打上标记，然后清空当前节点的懒标记。

简单来说：用不到孩子节点时，就不更新；用到的时候，再把之前的修改一次性传递下去，这就是懒标记的精髓。

2.2 懒标记的适用前提

懒标记并不是万能的，它有一个关键的适用前提：对区间的修改操作必须是 "可批量执行" 的，即能在 O (1) 时间内根据区间长度计算出修改后的区间信息。

比如 "区间所有元素加 k" 满足这个条件：区间和 = 原区间和 + 区间长度 * k；但如果是 "区间所有元素取平方"，就无法在 O (1) 时间内批量计算区间和，也就无法用懒标记，这一点需要特别注意。

三、带懒标记的线段树结构设计

要实现区间修改，我们需要对基础线段树的节点结构进行扩展，在原有基础上增加懒标记变量 ，同时新增**pushdown（下发懒标记）和lazy（更新当前节点并打标记）两个核心函数，配合原有的pushup（整合孩子信息）、build（建树）、modify（修改）、query（查询）**完成整体逻辑。

以下面这张图为例：

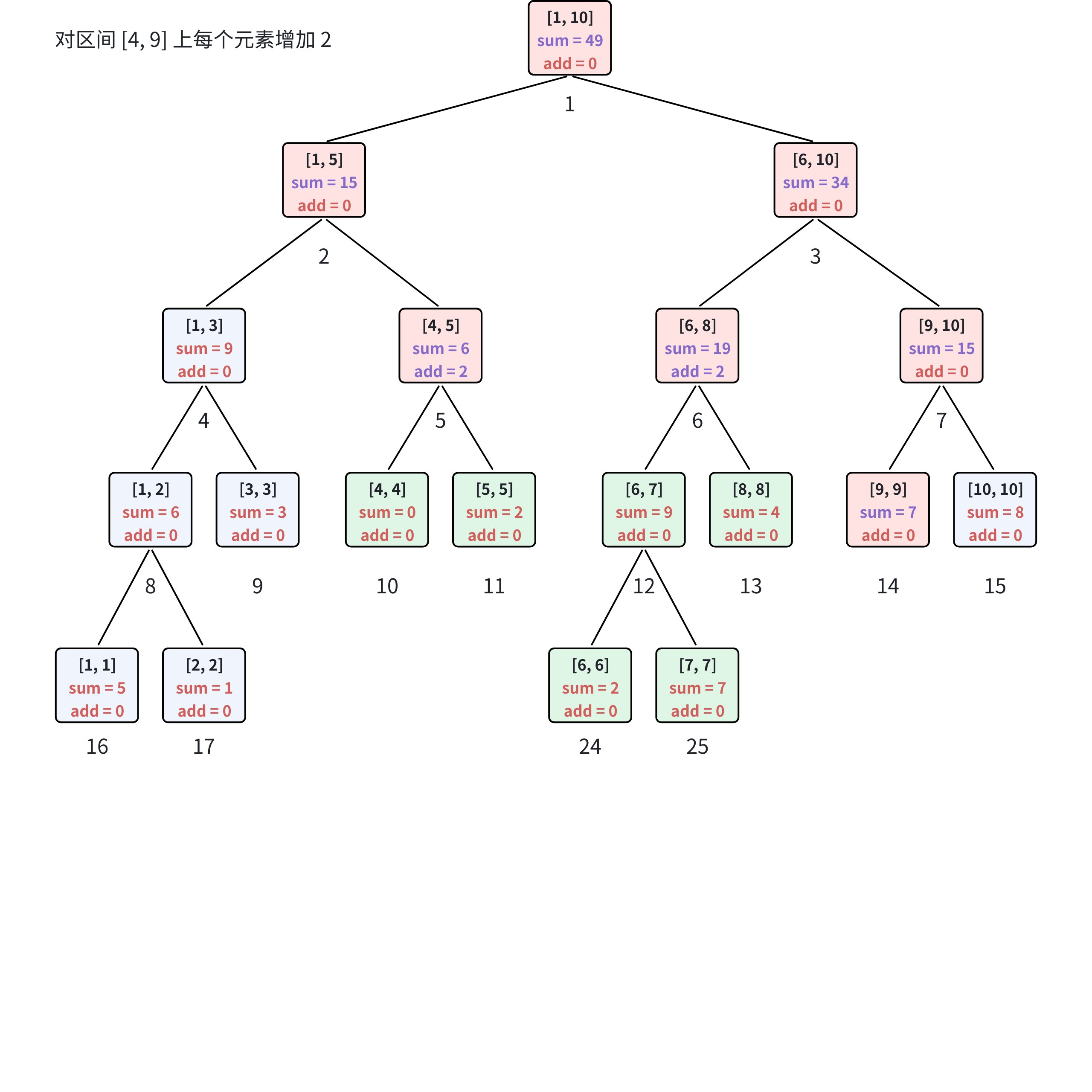
如果执行查询操作，则维护的信息如下：

3.1 节点结构体定义

以维护区间和为例，我们的节点需要包含以下四个信息：

l/r：当前节点维护的区间左右端点；

sum：当前节点维护的区间和；

add：懒标记，记录当前区间的所有元素需要加的数值，初始值为 0（表示无标记）。

C++ 代码实现：

cpp 复制代码

typedef long long LL;
const int N = 1e5 + 10;
// 线段树空间开4倍，避免越界
struct node
{
    int l, r;
    LL sum, add;
}tr[N * 4];
LL a[N]; // 原始数组

注意：线段树的空间必须开原始数组最大长度的 4 倍，这是线段树静态实现的固定要求，避免递归时节点编号越界。

3.2 核心辅助函数设计

带懒标记的线段树有三个核心辅助函数，分别是pushup、lazy、pushdown，这三个函数是整个实现的灵魂，我们逐个讲解。

3.2.1 pushup：整合左右孩子的信息

pushup是基础线段树就有的函数，作用是用左右孩子的信息更新当前节点的信息 ，对于区间和来说，就是当前节点的和 = 左孩子的和 + 右孩子的和。

这个函数的逻辑不会因为懒标记而改变，代码实现：

cpp 复制代码

// 整合左右孩子的区间和，更新当前节点
void pushup(int p)
{
    tr[p].sum = tr[p << 1].sum + tr[p << 1 | 1].sum;
}

其中p << 1是左孩子节点编号，p << 1 | 1是右孩子节点编号，这是线段树静态存储的标准写法。

3.2.2 lazy：更新当前节点并打上懒标记

lazy函数的作用是对当前节点的整个区间执行批量修改，更新节点信息并打上懒标记，是实现 "延迟更新" 的关键。

以 "区间加 k" 为例，逻辑分为两步：

更新当前节点的区间和：sum += (r - l + 1) * k（区间长度 * 每次加的数值）；

更新当前节点的懒标记：add += k（记录这个区间的所有元素需要加 k）。

代码实现：

cpp 复制代码

// 对节点p维护的区间执行加k操作，更新信息并打标记
void lazy(int p, LL k)
{
    auto& t = tr[p];
    t.sum += (t.r - t.l + 1) * k;
    t.add += k;
}

这里用 C++ 的引用**auto& t = tr[p]**是为了简化代码，避免重复写tr[p]。

3.2.3 pushdown：下发懒标记到左右孩子

pushdown是懒标记特有的函数，作用是将当前节点的懒标记下发给左右孩子，更新孩子的信息并给孩子打标记，然后清空当前节点的懒标记。

这个函数只有在当前节点有懒标记（add != 0） ，且当前节点不是叶子节点时才需要执行，核心逻辑分为三步：

把懒标记下发给左孩子：调用lazy函数，给左孩子加tr[p].add；

把懒标记下发给右孩子：调用lazy函数，给右孩子加tr[p].add；

清空当前节点的懒标记：将tr[p].add置为 0，表示当前节点的修改已经全部下发。

代码实现：

cpp 复制代码

// 下发懒标记到左右孩子
void pushdown(int p)
{
    if (tr[p].add) // 只有有标记时才需要下发
    {
        // 下发给左孩子和右孩子
        lazy(p << 1, tr[p].add);
        lazy(p << 1 | 1, tr[p].add);
        // 清空当前节点的标记
        tr[p].add = 0;
    }
}

关键注意点 ：pushdown必须在递归访问孩子节点之前 执行，比如修改或查询时，如果需要深入到左右孩子，必须先执行pushdown，确保孩子节点的信息是最新的。

四、带懒标记的线段树核心操作实现

有了节点结构和核心辅助函数，我们接下来实现线段树的建树、区间修改 、区间查询 三个核心操作，这三个操作是在基础版本上做了懒标记的适配，核心变化是在递归访问孩子前增加了**pushdown**。

4.1 build：建树操作

建树的逻辑和基础线段树基本一致，递归将区间一分为二，直到叶子节点（l == r），此时叶子节点的和就是原始数组的对应值，懒标记初始为 0；非叶子节点递归构建左右孩子后，调用**pushup**整合信息。

代码实现：

cpp 复制代码

// 建树：p是当前节点编号，l/r是当前节点维护的区间
void build(int p, int l, int r)
{
    tr[p] = {l, r, a[l], 0}; // 懒标记初始为0
    if (l == r) return; // 叶子节点，直接返回
    int mid = (l + r) >> 1; // 区间中点
    build(p << 1, l, mid); // 构建左孩子
    build(p << 1 | 1, mid + 1, r); // 构建右孩子
    pushup(p); // 整合左右孩子的信息
}

调用方式 ：build(1, 1, n)，表示从根节点（编号 1）开始，构建维护 [1,n] 区间的线段树（数组下标从 1 开始，方便线段树操作）。

4.2 modify：区间修改操作

区间修改是本文的核心，实现**"对 [x,y] 区间内的所有元素加 k"** ，逻辑分为三步，全程遵循 **"先判断，再下发，后递归"**的原则：

如果当前节点的区间被 [x,y] 完全覆盖 ：直接调用lazy函数更新当前节点并打标记，返回（无需递归到孩子）；

如果未被完全覆盖 ：先执行pushdown下发懒标记（确保孩子节点信息最新）；

递归修改左右孩子 ：判断当前节点的左孩子、右孩子是否与 [x,y] 有重叠，有重叠则递归修改，修改完成后调用pushup整合孩子的新信息。

代码实现：

cpp 复制代码

// 区间修改：对[x,y]区间的所有元素加k，p是当前节点编号
void modify(int p, int x, int y, LL k)
{
    auto& t = tr[p];
    // 情况1：当前节点区间被[x,y]完全覆盖，直接打标记
    if (x <= t.l && t.r <= y)
    {
        lazy(p, k);
        return;
    }
    // 情况2：未完全覆盖，先下发标记
    pushdown(p);
    int mid = (t.l + t.r) >> 1;
    // 左孩子与[x,y]有重叠，递归修改左孩子
    if (x <= mid) modify(p << 1, x, y, k);
    // 右孩子与[x,y]有重叠，递归修改右孩子
    if (y > mid) modify(p << 1 | 1, x, y, k);
    // 整合左右孩子的新信息
    pushup(p);
}

这个逻辑的时间复杂度是O (logn)，因为即使需要递归，也只涉及线段树的两条路径，和单点修改的复杂度一致。

4.3 query：区间查询操作

区间查询的目标是 "查询 [x,y] 区间的和" ，逻辑和区间修改类似，同样遵循**"先判断，再下发，后递归"**的原则，核心步骤：

如果当前节点的区间被 [x,y] 完全覆盖：直接返回当前节点的和（信息是最新的）；

如果未被完全覆盖 ：先执行pushdown下发懒标记（确保孩子节点信息最新）；

递归查询左右孩子：判断左、右孩子是否与 [x,y] 有重叠，有重叠则累加查询结果，最终返回累加值。

代码实现：

cpp 复制代码

// 区间查询：查询[x,y]区间的和，p是当前节点编号
LL query(int p, int x, int y)
{
    auto& t = tr[p];
    // 情况1：当前节点区间被[x,y]完全覆盖，直接返回和
    if (x <= t.l && t.r <= y)
    {
        return t.sum;
    }
    // 情况2：未完全覆盖，先下发标记
    pushdown(p);
    int mid = (t.l + t.r) >> 1;
    LL res = 0;
    // 左孩子与[x,y]有重叠，累加左孩子的查询结果
    if (x <= mid) res += query(p << 1, x, y);
    // 右孩子与[x,y]有重叠，累加右孩子的查询结果
    if (y > mid) res += query(p << 1 | 1, x, y);
    return res;
}

查询的时间复杂度依然是O (logn)，因为懒标记的下发只在需要时执行，不会增加额外的时间开销。

五、完整实战代码：洛谷 P3372【模板】线段树 1

题目链接：https://www.luogu.com.cn/problem/P3372

理论讲完，我们结合洛谷的经典模板题P3372【模板】线段树 1来写完整的实战代码，题目要求实现 "区间加 k" 和 "区间查询和"，正好是我们本文讲解的内容，先看题目要求：

题目描述

已知一个数列，需要进行两种操作：

将某区间每一个数加上 k；
求出某区间每一个数的和。

输入输出格式

输入：第一行 n 和 m（数列长度和操作次数）；第二行 n 个初始值；接下来 m 行，每行是操作 1（1 x y k）或操作 2（2 x y）。
输出：对于每个操作 2，输出对应的区间和。

完整 AC 代码

结合本文的实现，写出完整的 C++ 代码，注意数据范围用long long避免溢出，数组下标从 1 开始：

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;

// 线段树节点结构：l/r区间，sum区间和，add懒标记
struct node
{
    int l, r;
    LL sum, add;
}tr[N * 4];

LL a[N]; // 原始数组

// 整合左右孩子信息，更新当前节点
void pushup(int p)
{
    tr[p].sum = tr[p << 1].sum + tr[p << 1 | 1].sum;
}

// 对节点p执行加k操作，更新信息并打懒标记
void lazy(int p, LL k)
{
    auto& t = tr[p];
    t.sum += (t.r - t.l + 1) * k;
    t.add += k;
}

// 下发懒标记到左右孩子
void pushdown(int p)
{
    if (tr[p].add)
    {
        lazy(p << 1, tr[p].add);
        lazy(p << 1 | 1, tr[p].add);
        tr[p].add = 0;
    }
}

// 建树：p节点维护[l,r]区间
void build(int p, int l, int r)
{
    tr[p] = {l, r, a[l], 0};
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(p << 1, l, mid);
    build(p << 1 | 1, mid + 1, r);
    pushup(p);
}

// 区间修改：[x,y]区间加k
void modify(int p, int x, int y, LL k)
{
    auto& t = tr[p];
    if (x <= t.l && t.r <= y)
    {
        lazy(p, k);
        return;
    }
    pushdown(p);
    int mid = (t.l + t.r) >> 1;
    if (x <= mid) modify(p << 1, x, y, k);
    if (y > mid) modify(p << 1 | 1, x, y, k);
    pushup(p);
}

// 区间查询：查询[x,y]区间和
LL query(int p, int x, int y)
{
    auto& t = tr[p];
    if (x <= t.l && t.r <= y)
    {
        return t.sum;
    }
    pushdown(p);
    int mid = (t.l + t.r) >> 1;
    LL res = 0;
    if (x <= mid) res += query(p << 1, x, y);
    if (y > mid) res += query(p << 1 | 1, x, y);
    return res;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0); // 加速cin，避免超时

    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }
    build(1, 1, n); // 根节点1，维护[1,n]

    while (m--)
    {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1)
        {
            LL k;
            cin >> k;
            modify(1, x, y, k);
        }
        else
        {
            cout << query(1, x, y) << endl;
        }
    }

    return 0;
}

代码优化点 ：加入**ios::sync_with_stdio(false); cin.tie(0);**加速输入输出，避免在数据量大时 cin 超时，这是算法竞赛中 C++ 的常用优化技巧。

六、懒标记的核心易错点总结

懒标记的实现看似简单，但实际写代码时很容易踩坑，笔者结合自己的学习经验和刷题经历，总结了几个最容易出错的点，一定要注意：

6.1 忘记在修改 / 查询前执行 pushdown

这是最常见的错误，比如在区间修改时，未完全覆盖当前节点却直接递归孩子，此时孩子节点的信息还是旧的，会导致查询结果错误。只要需要递归访问孩子节点，必须先执行 pushdown。

6.2 lazy 函数只打标记，不更新当前节点信息

比如只写tr[p].add += k，却忘记更新**tr[p].sum**，会导致当前节点的信息错误，后续的查询操作直接取到错误的和，这是致命错误。

6.3 pushdown 后未清空当前节点的懒标记

如果下发标记后不把**tr[p].add**置为 0，会导致后续操作重复下发标记，同一个修改被执行多次，结果必然错误。

6.4 线段树空间开得不够

线段树的静态实现必须开4 倍的原始数组空间，比如 n=1e5 时，tr 数组要开 4*1e5=4e5，否则会出现数组越界，程序崩溃。

6.5 数据类型溢出

区间和的数值可能非常大，比如 n=1e5，每个数是 1e9，区间和就是 1e14，必须用long long类型存储 sum 和 add，用 int 会直接溢出，这是算法竞赛的基础细节。

6.6 叶子节点执行 pushdown

叶子节点没有左右孩子，执行 pushdown 不会有实际效果，但不会报错，属于冗余操作，可加判断优化，但不影响正确性。

七、懒标记的扩展思考：不止于区间加

本文讲解的是 "区间加 k" 的懒标记实现，但懒标记的思想可以扩展到其他可批量执行的区间修改操作，比如：

区间赋值 ：将 [x,y] 区间的所有元素赋值为 k，此时懒标记可以用一个变量set表示，初始为 - 1（无标记），lazy函数的逻辑是*sum = (r-l+1)k，set = k；

区间乘 k ：将 [x,y] 区间的所有元素乘 k，懒标记用mul表示，初始为 1，lazy函数的逻辑是**sum = k，mul = k；

区间加 k + 区间乘 k ：组合操作，此时需要两个懒标记，且要注意操作的优先级（先乘后加，避免精度损失）。

这些扩展操作的核心思想和本文的 "区间加 k" 一致，都是**"延迟更新，按需下发"**，只是lazy和pushdown的函数逻辑需要根据修改操作调整。

比如区间赋值的懒标记实现，只需要修改lazy和pushdown：

cpp 复制代码

// 区间赋值的lazy函数：将节点p的区间赋值为k
void lazy(int p, LL k)
{
    auto& t = tr[p];
    t.sum = (t.r - t.l + 1) * k;
    t.set = k; // set是赋值的懒标记，初始为-1
}

// 区间赋值的pushdown函数
void pushdown(int p)
{
    if (tr[p].set != -1)
    {
        lazy(p << 1, tr[p].set);
        lazy(p << 1 | 1, tr[p].set);
        tr[p].set = -1;
    }
}

可见，只要掌握了懒标记的核心思想，各种扩展操作都可以轻松实现。

总结

懒标记是线段树进阶的核心，它让线段树从 "只能高效处理单点修改" 升级为 "能高效处理区间修改"，成为处理区间问题的终极利器。本文从问题痛点出发，拆解了懒标记 "延迟更新，按需下发" 的核心思想，手把手实现了带懒标记的线段树，并结合洛谷模板题给出了完整的实战代码，总结了核心易错点。

最后用一句话总结懒标记的学习要点：理解 "为什么延迟"，掌握 "怎么标记"，牢记 "何时下发"。懒标记的代码模板并不复杂，但需要通过大量的刷题来熟练运用，比如洛谷的 P3368、P1816、P3870 等题目，都是练习懒标记的好题。

掌握了懒标记，你就真正踏入了线段树的大门，后续的线段树 + 分治、线段树 + 剪枝、权值线段树等进阶内容，都可以在此基础上轻松学习。希望本文能帮助你彻底吃透线段树的区间修改，在算法竞赛和数据结构实战中所向披靡！

创作不易，如果本文对你有帮助，欢迎点赞、收藏、关注三连～

【算法提高篇】（二）线段树之区间修改：懒标记的核心奥义与实战实现

目录

前言

一、为什么基础线段树处理区间修改会 "拉胯"？

二、懒标记的核心设计思想："延迟更新，按需下发"

2.1 核心思路拆解

2.2 懒标记的适用前提

三、带懒标记的线段树结构设计

3.1 节点结构体定义

3.2 核心辅助函数设计

3.2.1 pushup：整合左右孩子的信息

3.2.2 lazy：更新当前节点并打上懒标记

3.2.3 pushdown：下发懒标记到左右孩子

四、带懒标记的线段树核心操作实现

4.1 build：建树操作

4.2 modify：区间修改操作

4.3 query：区间查询操作

五、完整实战代码：洛谷 P3372【模板】线段树 1

题目描述

输入输出格式

完整 AC 代码

六、懒标记的核心易错点总结

6.1 忘记在修改 / 查询前执行 pushdown

6.2 lazy 函数只打标记，不更新当前节点信息

6.3 pushdown 后未清空当前节点的懒标记

6.4 线段树空间开得不够

6.5 数据类型溢出

6.6 叶子节点执行 pushdown

七、懒标记的扩展思考：不止于区间加

总结