1.基本原理
1.1. 社会等级制度 (Social Hierarchy)
GWO 将狼群严格划分为四个等级,用以模拟寻优过程中的领导力:
Alpha (α): 领头狼,代表当前找到的最优解。负责决策。
Beta (β): 副手,代表第二优解。协助 Alpha 决策。
Delta (δ): 侦察兵、捕食者等,代表第三优解。负责执行指令。
Omega (ω): 底层狼,代表其他候选解。它们必须服从上述三者的指引。
1.2. 捕猎机制 (Hunting Mechanism)
算法通过模拟以下三个主要步骤来寻找全局最优解:
包围 (Encircling): 狼群根据猎物(目标点)的位置更新自己的位置。
狩猎 (Hunting): 认为 α、β 和 δ 对猎物潜在位置有更好的认知。其他狼(ω)根据这前三者的位置更新自己的坐标。
攻击 (Attacking): 通过调整参数,算法在探索(寻找新区域)和开发(精细搜索已知区域)之间取得平衡。
2.代码实现
python
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
def objective_function(x):
d = len(x)
shift = 1.5
z = x - shift
z_rotated = np.copy(z)
for i in range(1, d):
z_rotated[i] = z[i] + 0.5 * z[i-1]
return 10 * d + np.sum(z_rotated**2 - 10 * np.cos(2 * np.pi * z_rotated))
class GWO:
def __init__(self, obj_func, dim, search_range, num_wolves=30, max_iter=100):
self.obj_func = obj_func
self.dim = dim
self.lb, self.ub = search_range
self.num_wolves = num_wolves
self.max_iter = max_iter
self.positions = np.random.uniform(self.lb, self.ub, (num_wolves, dim))
self.alpha_pos = np.zeros(dim)
self.alpha_score = float("inf")
self.beta_pos, self.beta_score = np.zeros(dim), float("inf")
self.delta_pos, self.delta_score = np.zeros(dim), float("inf")
self.convergence_curve = []
def optimize(self):
for t in range(self.max_iter):
for i in range(self.num_wolves):
self.positions[i] = np.clip(self.positions[i], self.lb, self.ub)
fitness = self.obj_func(self.positions[i])
if fitness < self.alpha_score:
self.delta_score, self.delta_pos = self.beta_score, self.beta_pos.copy()
self.beta_score, self.beta_pos = self.alpha_score, self.alpha_pos.copy()
self.alpha_score, self.alpha_pos = fitness, self.positions[i].copy()
elif fitness < self.beta_score:
self.delta_score, self.delta_pos = self.beta_score, self.beta_pos.copy()
self.beta_score, self.beta_pos = fitness, self.positions[i].copy()
elif fitness < self.delta_score:
self.delta_score, self.delta_pos = fitness, self.positions[i].copy()
if t % 10 == 0:
print(f"Iteration {t}: Best Fitness = {self.alpha_score:.6f}")
a = 2 - t * (2 / self.max_iter)
for i in range(self.num_wolves):
for j in range(self.dim):
def get_X(p_pos, curr_pos, a_val):
r1, r2 = np.random.rand(), np.random.rand()
A, C = 2 * a_val * r1 - a_val, 2 * r2
D = abs(C * p_pos - curr_pos)
return p_pos - A * D
X1 = get_X(self.alpha_pos[j], self.positions[i, j], a)
X2 = get_X(self.beta_pos[j], self.positions[i, j], a)
X3 = get_X(self.delta_pos[j], self.positions[i, j], a)
self.positions[i, j] = (X1 + X2 + X3) / 3
self.convergence_curve.append(self.alpha_score)
return self.alpha_pos, self.alpha_score, self.convergence_curve
dim = 2
search_range = (-5, 5)
max_iter = 500
gwo = GWO(objective_function, dim, search_range, num_wolves=60, max_iter=max_iter)
best_pos, best_score, curve = gwo.optimize()
print("-" * 30)
print(f"最终优化结果:")
print(f"找到的最优坐标: {best_pos}")
print(f"最优得分: {best_score:.8f}")
fig = plt.figure(figsize=(16, 7))
ax1 = fig.add_subplot(1, 2, 1, projection='3d')
x = np.linspace(search_range[0], search_range[1], 100)
y = np.linspace(search_range[0], search_range[1], 100)
X, Y = np.meshgrid(x, y)
Z = np.zeros(X.shape)
for i in range(X.shape[0]):
for j in range(X.shape[1]):
Z[i, j] = objective_function(np.array([X[i, j], Y[i, j]]))
surf = ax1.plot_surface(X, Y, Z, cmap=cm.coolwarm, alpha=0.6, antialiased=True)
ax1.scatter(best_pos[0], best_pos[1], best_score, color='red', marker='*', s=200, label='GWO Best Point', zorder=20)
ax1.plot([best_pos[0], best_pos[0]], [best_pos[1], best_pos[1]], [0, best_score], color='black', linestyle='--', linewidth=1.5)
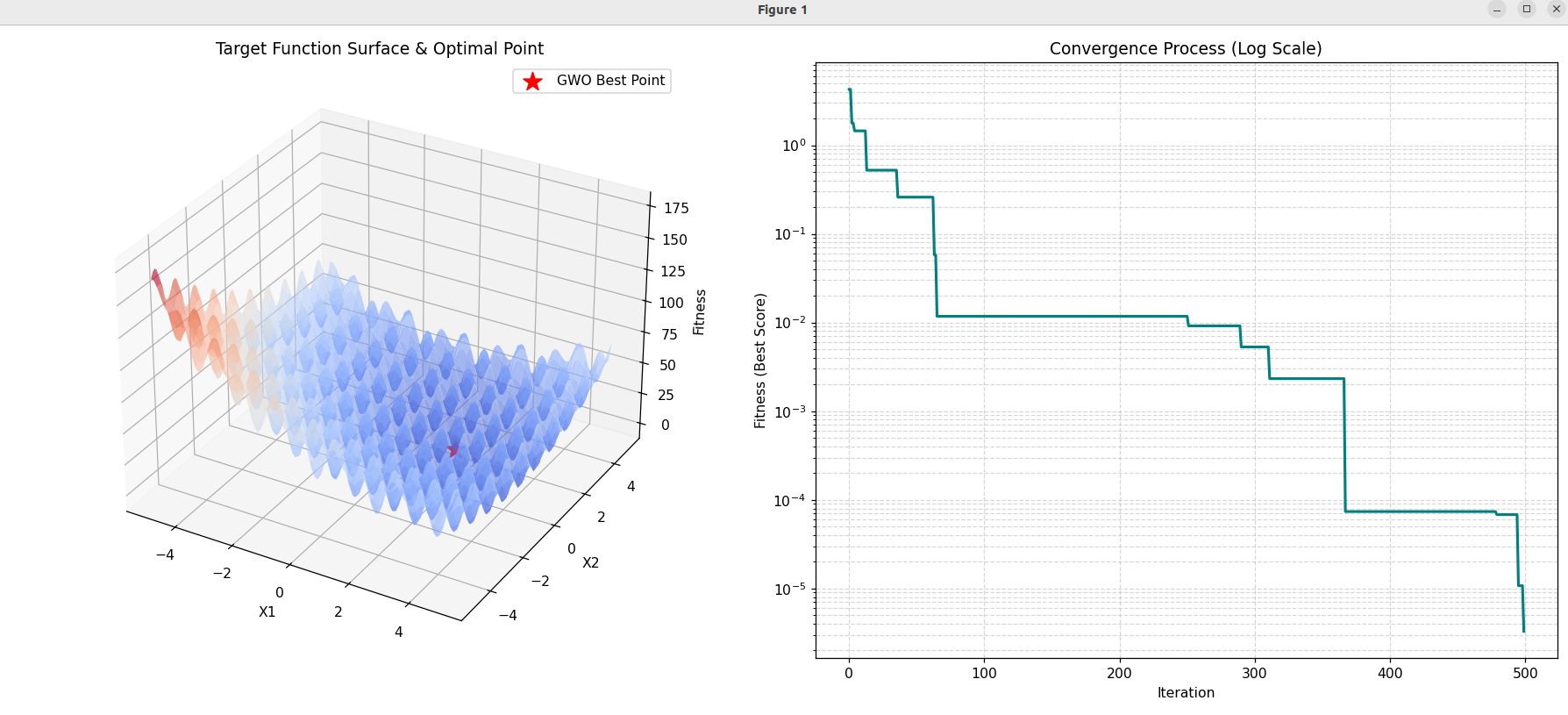
ax1.set_title("Target Function Surface & Optimal Point", fontsize=12)
ax1.set_xlabel('X1')
ax1.set_ylabel('X2')
ax1.set_zlabel('Fitness')
ax1.legend()
ax2 = fig.add_subplot(1, 2, 2)
ax2.semilogy(curve, color='teal', linewidth=2)
ax2.set_title("Convergence Process (Log Scale)", fontsize=12)
ax2.set_xlabel("Iteration")
ax2.set_ylabel("Fitness (Best Score)")
ax2.grid(True, which="both", linestyle='--', alpha=0.5)
plt.tight_layout()
plt.show()运行效果
bash
Iteration 0: Best Fitness = 14.571307
Iteration 10: Best Fitness = 1.144426
Iteration 20: Best Fitness = 0.143754
Iteration 30: Best Fitness = 0.143754
Iteration 40: Best Fitness = 0.143754
Iteration 50: Best Fitness = 0.031024
Iteration 60: Best Fitness = 0.031024
Iteration 70: Best Fitness = 0.031024
Iteration 80: Best Fitness = 0.031024
Iteration 90: Best Fitness = 0.031024
Iteration 100: Best Fitness = 0.031024
Iteration 110: Best Fitness = 0.002521
Iteration 120: Best Fitness = 0.002521
Iteration 130: Best Fitness = 0.002521
Iteration 140: Best Fitness = 0.002521
Iteration 150: Best Fitness = 0.002521
Iteration 160: Best Fitness = 0.002521
Iteration 170: Best Fitness = 0.002521
Iteration 180: Best Fitness = 0.002521
Iteration 190: Best Fitness = 0.002521
Iteration 200: Best Fitness = 0.002521
Iteration 210: Best Fitness = 0.002521
Iteration 220: Best Fitness = 0.002521
Iteration 230: Best Fitness = 0.002521
Iteration 240: Best Fitness = 0.002521
Iteration 250: Best Fitness = 0.002521
Iteration 260: Best Fitness = 0.002521
Iteration 270: Best Fitness = 0.002521
Iteration 280: Best Fitness = 0.002521
Iteration 290: Best Fitness = 0.002521
Iteration 300: Best Fitness = 0.002521
Iteration 310: Best Fitness = 0.002521
Iteration 320: Best Fitness = 0.002521
Iteration 330: Best Fitness = 0.000500
Iteration 340: Best Fitness = 0.000500
Iteration 350: Best Fitness = 0.000500
Iteration 360: Best Fitness = 0.000500
Iteration 370: Best Fitness = 0.000500
Iteration 380: Best Fitness = 0.000500
Iteration 390: Best Fitness = 0.000500
Iteration 400: Best Fitness = 0.000500
Iteration 410: Best Fitness = 0.000500
Iteration 420: Best Fitness = 0.000500
Iteration 430: Best Fitness = 0.000500
Iteration 440: Best Fitness = 0.000500
Iteration 450: Best Fitness = 0.000500
Iteration 460: Best Fitness = 0.000500
Iteration 470: Best Fitness = 0.000403
Iteration 480: Best Fitness = 0.000403
Iteration 490: Best Fitness = 0.000086
------------------------------
最终优化结果:
找到的最优坐标: [1.500069 1.50001847]
最优得分: 0.00000150