leetcode hot100 236.二叉树的最近公共祖先 medium dfs 递归

---

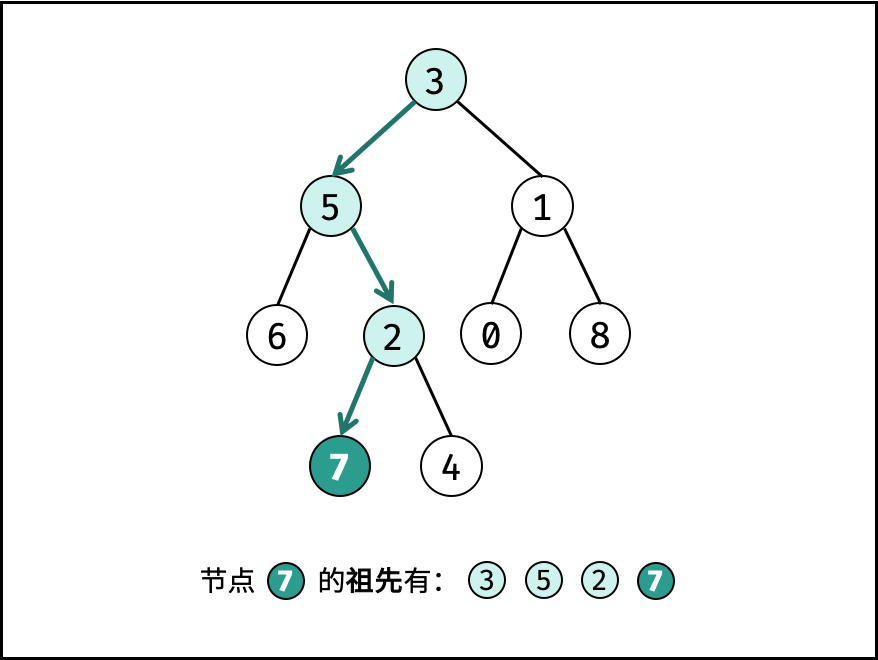
若 root 是 p,q 的 最近公共祖先 ，则只可能为以下情况之一：

1. p 和 q 在 root 的子树中，且分列 root 的 异侧（即分别在左、右子树中）
2. p=root ，且 q 在 root 的左或右子树中；
3. q=root ，且 p 在 root 的左或右子树中；

---

向下递归，向上回溯，首个同时包含 p 和 q 的节点为答案

在 DFS 回溯的过程中，每个节点都向它的父节点汇报情况："我这棵子树里有没有发现 ppp 或者 qqq？"

1. 如果我就是 ppp 或者 qqq，我直接把自己汇报上去。
2. 如果我的左子树发现了，右子树也发现了，那我就是那个"首个同时包含"的最近公共祖先
3. 如果只有一边发现了，我就把发现的那个ppp 或者 qqq，继续往上传。
4. 都没发现？汇报 None。

---

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        # 每个节点都向它的父节点汇报："我这棵子树里有没有发现p、q？"
        # 1. 终止条件：我没有子节点； or 我就是p、q
        if not root or root==p or root==q:
            return root

        # 2. 我不是p、q，那我的左右子树是不是？向下递归
        # Solution里的def A里调A: self.A
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)

        # 3. 向上回溯：根据子树的汇报结果做判断
        # 情况 A：左右子树都汇报了结果（一个发现了 p，一个发现了 q）
        # 说明当前节点就是最近公共祖先！
        if left and right:
            return root

        # 情况 B：只有左子树汇报了结果
        # 说明 p 和 q 都在左边，或者只找到了其中一个，先传上去再说
        if left:
            return left 

        # 情况 C：只有右子树汇报了结果
        if right:
            return right

        # 情况 D：都没找到
        return None    
          

时间复杂度 O(N) ：

在最坏的情况下（比如目标节点 ppp 或 qqq 不存在，或者它们是树中最深的叶子节点），我们需要遍历二叉树中的每一个节点。每个节点只会被访问一次。在每个节点上，我们只进行了常数时间的逻辑判断（判断是否等于 ppp、qqq，以及合并左右子树的汇报结果）。
空间复杂度 O(N) ：

最坏情况：当二叉树退化成一个链表（高度 H=NH = NH=N）时，递归的深度会达到 NNN，此时系统栈需要 O(N)O(N)O(N) 的空间。

最好情况：当二叉树是完全平衡的，树的高度 H=log⁡NH = \log NH=logN。此时递归深度最小，空间复杂度为 O(log⁡N)O(\log N)O(logN)。