Dijstra算法学习笔记

随意起个昵称2026-02-16 12:06

1 Dijkstra算法解决的问题

Dijkstra算法是是一种求解非负权图 上单源最短路径的算法。在有n个顶点的非负权图上，从起始点出发，采用贪心算法的策略，每次找到距离起始点最近且未被访问过 的节点v，做访问标记，然后以点v做为中间节点更新与v相邻且未被访问的节点到起始点的最短路径。由于每次都会找到并标记一个距离起始点最近的节点，因此经过n-1轮上述操作，所有的点都可以找到离起始点的最短距离（因为第n轮剩一个点未被标记，这个点做中转点意义不大）。模板题可参考洛谷P4779。

2 Dijkstra朴素算法

2.1 算法过程

  1. 初始化：起始点到起始点的最短距离为0，起始点到其他点的最短距离为一个很大很大的值。
  2. 找到一个未被标记的、离起始点最近的点u，然后标记点u。
  3. 扫描节点u的所有出边(u,v,w),如果以点u作为中转点使得起始点到点v的最短距离更小，则更新起始点到点v的最短距离。
  4. 重复2和3，直至所有节点都被标记。

下面借用董晓老师的图来说一下：

2.1.1 图解过程

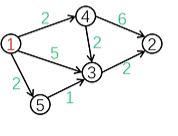
比如在上图中，要找从点1出发到各点的最短距离
第1轮： 可以看到点1到点1的距离最近，标记点1。然后看以点1作为中转点，扫描节点1的所有出边,更新相应节点的最短距离。图中可以看出，以点1为中转点，点1到点4的最短距离被更新为2，点1到点5的最短距离被更新为2，点1到点3的最短距离被更新为5。
第2轮： 点1到点4的距离最近（下一轮选点5，点4和点5标记的先后顺序影响不大），标记点4。然后看以点4作为中转点，扫描节点4的所有出边,更新相应节点的最短距离。图中可以看出，以点4为中转点，点1到点2的最短距离被更新为8，点1到点3的最短距离被更新为4。
第3轮： 可以看到点1到点5的距离最近，标记点5。然后看以点5作为中转点，扫描节点5的所有出边,更新相应节点的最短距离。图中可以看出，以点5为中转点，点1到点3的最短距离被更新为3。
第4轮： 可以看到点1到点3的距离最近，标记点3。然后看以3作为中转点，扫描节点3的所有出边,更新相应节点的最短距离。图中可以看出，以点3为中转点，点1到点2的最短距离被更新为5。

2.1.2 如果有负权边会怎样？

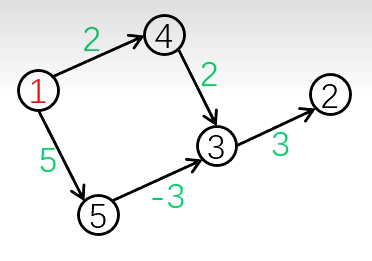
如上图所示，按照算法流程：
第1轮： 可以看到点1到点1的距离最近，标记点1。然后看以点1作为中转点，扫描节点1的所有出边,更新相应节点的最短距离。图中可以看出，以点1为中转点，点1到点4的最短距离被更新为2，点1到点5的最短距离被更新为5。
第2轮： 点1到点4的距离最近，标记点4。然后看以点4作为中转点，扫描节点4的所有出边,更新相应节点的最短距离。图中可以看出，以点4为中转点，点1到点3的最短距离被更新为4。
第3轮： 可以看到点1到点3的距离最近，标记点3。然后看以点3作为中转点，扫描节点3的所有出边,更新相应节点的最短距离。图中可以看出，以点3为中转点，点1到点2的最短距离被更新为7。
第4轮： 可以看到点1到点5的距离最近，标记点5。然后看以点5作为中转点，扫描节点5的所有出边,更新相应节点的最短距离。图中可以看出，以点5为中转点，我们发现点1到点3的距离可以更短，但是点3被标记过，忽略。

至此，n-1轮操作做完了，但是点1到点3的最短距离和点1和点2的最短距离都是不对的，因此不适用于用负权边的图。

2.2 代码实现

2.2.1 存储结构

我们可以根据题目选择邻接表或者邻接矩阵等存储图，使用一个一维数组d存储各点到起始点的最短路径。

在以点u为中转点更新起始点到点v的最短距离时，可以用表达式d[u]+w<d[v]表示，w为u到v的边权。

2.2.2 实现代码

使用邻接表存图的Dijkstra算法代码如下：

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
const int M=200005;
int n,m,d[M],s;
bool vis[M];
vector<pair<int,int> > g[M];
int main(){
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=m;i++){
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		g[u].push_back({v,w});
	}
	memset(d,0x3f,sizeof(d));
	d[s]=0;
	for(int i=1;i<=n-1;i++){
		int u=-1; //好好思考一下，嘻嘻
		for(int j=1;j<=n;j++){
			// 如果不把 u 初始化为-1，而是1-n的一个值有可能d[u]＜所有为访问过的d[j]就出错啦！
			if(vis[j]==0&&(u==-1||d[u]>d[j])) u=j;
		}
		vis[u]=1;
		for(int j=0;j<g[u].size();j++){
			int v=g[u][j].first,w=g[u][j].second;
			if(vis[v]==0&&d[u]+w<d[v]) 
				d[v]=d[u]+w;
		}
	}
	for(int i=1;i<=n;i++) printf("%d ",d[i]);
    return 0;
}

2.3 时间复杂度分析

2.2 中的代码提交到洛谷TLE了，因为上述代码时间复杂度为O(n2)量级的。更新最短距离需要n-1轮，内部第一个循环在找未被访问过且距离起始点最近的节点这个过程循环了n次，当n的数据规模达到10^5时，就超时了。内部第二个循环其实是在遍历每条边，n-1轮总时间复杂度为O(m)。我们优化的一个方向是把找未被访问过且距离起始点最近的节点的时间复杂度优化一下。

3 Dijkstra堆优化

3.1 优化方向

我们可以用优先队列去存储起始点到各顶点的最短距离。每次从优先队列中弹出距离起始点最短距离的点u的时间复杂度是O(logn)级别的（时间主要花在弹出后优先队列的维护），(n-1)次操作，时间复杂度为O(nlogn)级别的；以u为中转点，更新u邻接的点的最短距离，加入优先队列中，m条边如此操作，时间复杂度为O(mlogn)级别的。

这样，总时间复杂度为O((n+m)logn)级别的。比2.2 中的代码有较大的提升。

3.2 实现代码

3.2.1 实现细节

优先队列存储相邻节点和相应的边权，可以用STL的priority_queue去做，类型可以用pair<int,int>,priority_queue默认对第一个(first)从大到小排序。而我们每次要弹出的是最小的，所有我们加入队列时first对应的是边权的相反数，second对应的相邻节点。

当然也可以写结构体，然后用operator<去实现。

3.2.2 代码实现
cpp 复制代码 
#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=200005;
int n,m,s,a,b,c,d[N];
bool vis[N];
priority_queue< pair<int,int> > q;
vector< pair<int,int> > e[N];
void dij(int s){
	memset(d,0x3f,sizeof(d)); d[s]=0;
	q.push({0,s});
	while(q.size()){
		int u=q.top().second;
		q.pop();
		if(vis[u]) continue;
		vis[u]=1;
		for(int i=0;i<e[u].size();i++){
			int v=e[u][i].first;
			int w=e[u][i].second;
			if(d[u]+w<d[v]){
				d[v]=d[u]+w;
				q.push({-d[v],v});
			}
		}
	}
}
signed main(){
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&a,&b,&c);
		e[a].push_back({b,c});
	}
	dij(s);
	for(int i=1;i<=n;i++) printf("%d ",d[i]);
    return 0;
}

4 相关习题

题目1：最短路计数

这道题开一个数组d存储起始点到各顶点的最短距离，再开一个数组f记录起始点1到各顶点的最短路径的数量。对于中转节点u，如果d[u]+w<d[v],则f[v]=f[u]。如果d[u]+w==d[v],则f[v]=(f[v]+f[u])% 100003。代码如下：

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2000005;
int n,m,a,b,d[maxn],f[maxn];
bool vis[maxn];
vector< pair<int,int> > e[maxn];
priority_queue< pair<int,int> > q;
void dij(int s){
	memset(d,0x3f,sizeof(d));
	d[s]=0,f[s]=1;
	q.push({0,s});
	while(q.size()){
		int u=q.top().second;
		q.pop();
		if(vis[u]) continue;
		vis[u]=1;
		for(int i=0;i<e[u].size();i++){
			int v=e[u][i].first;
			int w=e[u][i].second;
			if(d[u]+w==d[v]) f[v]=(f[v]+f[u])% 100003;
			if(d[u]+w<d[v]){
				d[v]=d[u]+w;
				q.push({-d[v],v});
				f[v]=f[u];
			}
		}
	}
}
signed main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&a,&b);
		e[a].push_back({b,1});
		e[b].push_back({a,1});
	}
	dij(1);
	for(int i=1;i<=n;i++) printf("%d\n",f[i]);	
    return 0;
}

题目2

我想到的是一开始我们可以跑Dijkstra算法记录节点1到各点的最短距离，记录在d数组中。然后枚举所有的边加倍，去跑Dijkstra算法，更新答案。

后面看了题解后发现有更优的，如果加倍的边不在最短路径上，增量为0，不构成最短路径上的边可以不考虑，时间复杂度就优化了。我们可以先跑一边Dijkstra算法，记录最短路径的节点。枚举最短路径节点构成的边，更新最大增量。因为这道题是无向图，加倍从u到v的边的同时，也要加倍从v到u的边，因此用邻接矩阵存储更合适。

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=110;
const int INF=0x3f3f3f3f; 
int n,m,d[maxn],idx,ans,pre[maxn],mn,path[maxn];
int ee[maxn][maxn];
bool vis[maxn];
void dij(bool p){
	priority_queue< pair<int,int> > q;
	memset(d,INF,sizeof(d));
	memset(vis,0,sizeof(vis));
	d[1]=0;
	q.push({0,1});
	while(q.size()){
		int u=q.top().second;
		q.pop();
		if(vis[u]) continue;
		vis[u]=1;
		for(int i=1;i<=n;i++){
			int w=ee[u][i];
			if(vis[i]==0&&d[i]>d[u]+w){
				d[i]=d[u]+w;
				q.push({-d[i],i});
				if(p) pre[i]=u;
			}
		}
	}
	ans=max(ans,d[n]);
}
signed main(){
	scanf("%lld%lld",&n,&m);
	memset(ee,INF,sizeof(ee));
	for(int i=1;i<=n;i++) ee[i][i]=0;
	for(int i=1;i<=m;i++){
		int a,b,c;
		scanf("%lld%lld%lld",&a,&b,&c);
		ee[a][b]=c;
		ee[b][a]=c;
	}
	dij(1);
	mn=ans;
	int cnt=1;
	path[cnt]=n;
	for(int i=pre[n];i;i=pre[i]){
		++cnt;
		path[cnt]=i;
	}
	for(int i=2;i<=cnt;i++){
		int w=ee[path[i]][path[i-1]];
		ee[path[i]][path[i-1]]=w*2;
		ee[path[i-1]][path[i]]=w*2;
		dij(0);
		ee[path[i]][path[i-1]]=w;
		ee[path[i-1]][path[i]]=w;
	}
	printf("%lld",ans-mn);
    return 0;
}

题目3

这道题很有意思，我们初始化d数组为1.00，初始化每次转给对方钱的比率为100%，即手续费为0%。跑Dijkstra算法，d[v]=max(d[v],d[u]*w)。这里要注意int和double的转换以及输出的格式。同时因为优先队列每次弹出的是最高比率，所以加入时不用去相反数。AC代码如下：

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int n,m,s,a,b,c,t;
vector< pair<int,double> > e[N];
double d[N];
bool vis[N];
void dij(){
	d[s]=1.0;
	priority_queue< pair<double,int> > q;
	q.push({1.0,s});
	while(q.size()){
		int u=q.top().second;
		q.pop();
		if(vis[u]) continue;
		vis[u]=1;
		for(int i=0;i<e[u].size();i++){
			int v=e[u][i].first;
			double w=e[u][i].second;
			if(d[u]*w>d[v]){
				d[v]=d[u]*w;
				q.push({d[v],v});
			}
		}
	}
} 
int main(){
	cin>>n>>m;
	for(int i=0;i<m;i++){
		scanf("%d%d%d",&a,&b,&c);
		e[a].push_back({b,1-0.01*c});
		e[b].push_back({a,1-0.01*c});
	}
	cin>>s>>t;
	dij();
	printf("%.8lf",100.0/d[t]);
	return 0;
}
相关推荐
爱凤的小光1 小时前
VisionPro 3D工具(自我笔记)
笔记·计算机视觉·3d
lxl13071 小时前
C++算法（3）二分算法
数据结构·c++·算法
2301_805962932 小时前
TF卡烧录系统盘文件后损坏
笔记
lifallen2 小时前
笛卡尔树 (Cartesian Tree)
java·数据结构·算法
ab1515172 小时前
2.15完成105、106、110
数据结构·算法
Clarence Liu2 小时前
用大白话讲解人工智能(5) SVM支持向量机：找一条“最宽的分隔线“
人工智能·算法·支持向量机
dalong102 小时前
A27：图像九宫格分割程序
笔记·aardio
不想看见4042 小时前
N-Queens -- 回溯法 -- 力扣101算法题解笔记
java·数据结构·算法
袁气满满~_~2 小时前
深度学习笔记四
人工智能·笔记·深度学习
热门推荐
01PHP Error: 常见错误及其解决方法02openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南03GitHub 镜像站点04Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services05从零搭建一个 PHP 登录注册系统（含完整源码）06UV安装并设置国内源07配置 OpenClaw 使用 Ollama 本地模型08Android Studio Panda 1 正式版来了：JDK 终于不用手动配了，内存泄漏也有原生方案了09全面体验 Grok API 中转站（2025 · Grok 4 系列最新版）10MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法