1.二分查找

++二分算法的重点也是难点在于找出数组的二段性,二段性是指存在一个分界点,将整个区间严格划分为左右两端,左边全满足某一性质,右边全不满足(或相反),两段性质严格互斥,无交叉,无遗漏。++
这道题属于朴素二分算法。
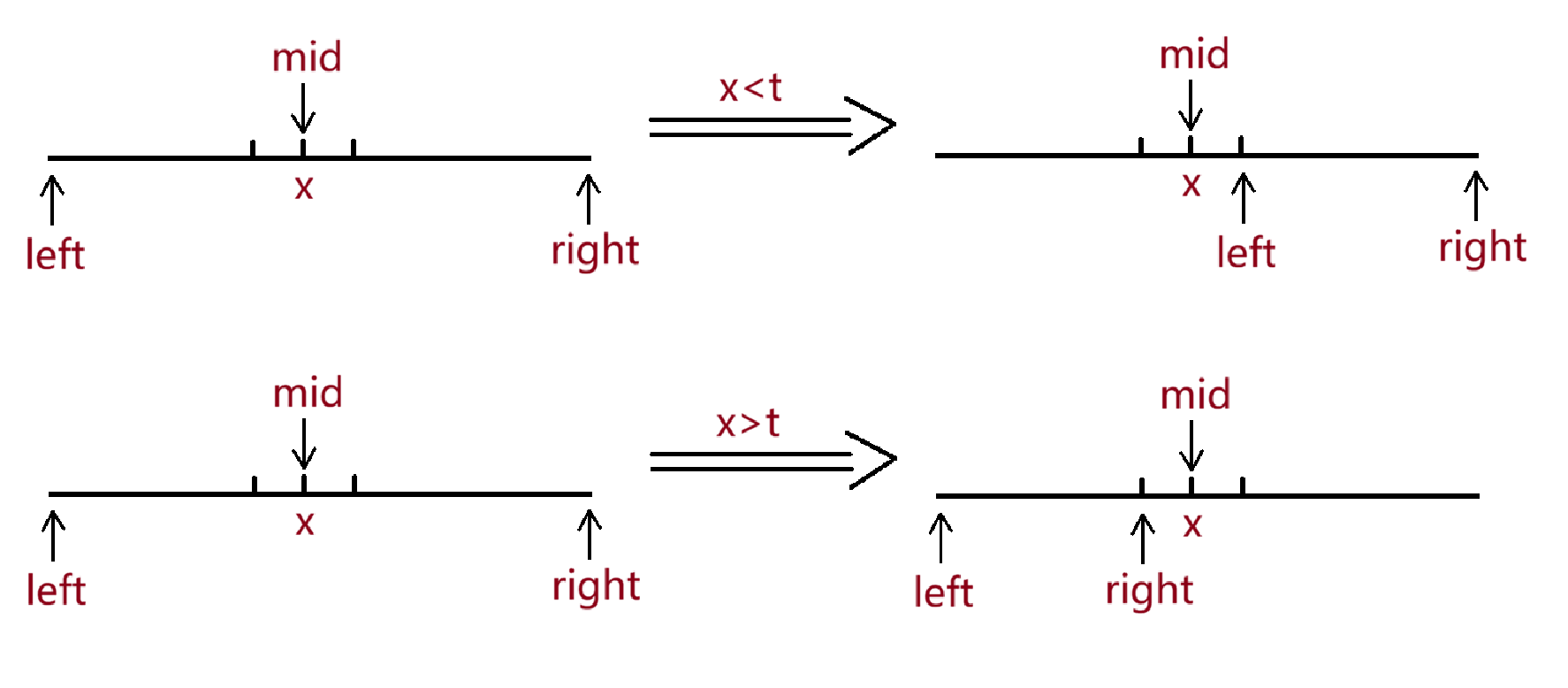
当x<target时,可知target在x右边,需要到右边去找,所以将left移至mid+1
当x>target时,可知target在x左边,需要到左边去找,所以将right移至mid-1
当x=target时,返回结果
注意循环结束条件为left>right,即循环条件为left<=right
二分算法的时间复杂度为:
当循环执行1次时,最多还需次循环
当循环执行2次时,最多还需次循环
当循环执行3次时,最多还需次循环
最坏情况下需要执行k次,还需次循环
解得
代码如下:
cpp
class Solution {
public:
int search(vector<int>& nums, int target)
{
int mid=0,left=0,right=nums.size()-1;
while(left<=right)
{
mid=left+(right-left)/2;
if(nums[mid]>target)
{
right=mid-1;
}
else if(nums[mid]<target)
{
left=mid+1;
}
else
return mid;
}
return -1;
}
};朴素二分查找模板:
cpp
while(left<=right)
{
int mid=left+(right-left)/2;
if(......)
left=mid+1;
else if(......)
right=mid-1;
else
return ......;
}int mid=left+(right-left)/2;
这是防溢出的写法,原先(left+right)/2 若加数太大会导致溢出。
另外left+(right-left)/2也等价于left+(right-left+1)/2,这两种写法在数组元素个数为奇数时没有区别,而在数组元素个数为偶数时只是取右边的中点还是左边的中点的区别
2.在排序数组中查找元素的第一个和最后一个位置
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)

暴力解法的时间复杂度为,在数组中全是目标元素的情况下,朴素二分查找的时间复杂度也是
,要找更优的算法
①查找区间的左端点:
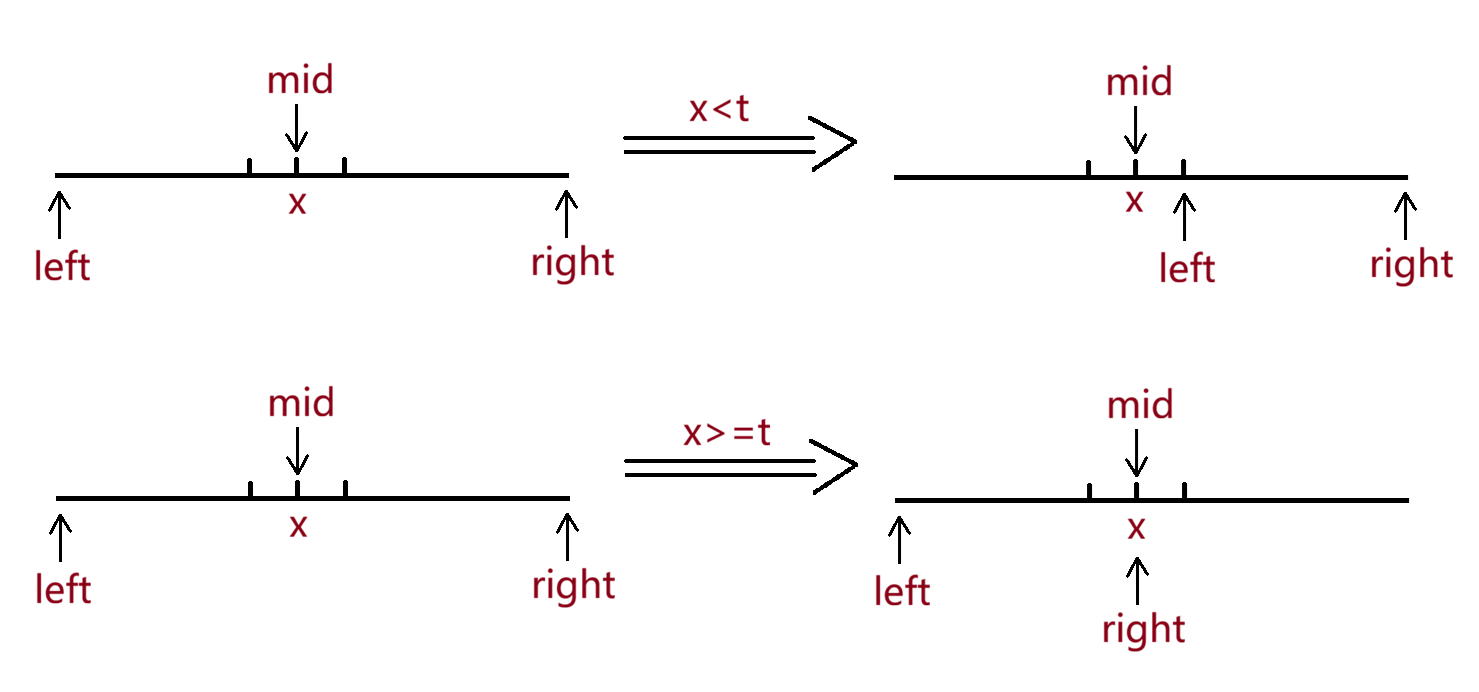
当x<target时,将left移至mid+1
当x>=target时,将right移至mid
循环条件:left<right
1>数组中有结果时:right最终停留在mid处,left跳出[left,mid-1]的区域和right站在同一位置,此时所指位置即为ret,无需再判断进入循环,否则死循环
2>数组元素全大于target时,right不断左移直至和left重合,此时已到边界,只需判断一下当前的值是否为target
3>数组元素全小于target时,left不断右移直至和right重合,此时已到边界,只需判断一下当前的值是否为target
求中点的操作:left+(right-left)/2当为left+(right-left)/2时,
,若x<t,left==right,退出循环,若x>=t,left==right,退出循环。符合要求。
当为left+(right-left+1)/2时,
,若x>=t,那么right一直==mid,进入死循环。不符合要求。
②查找区间的右端点:
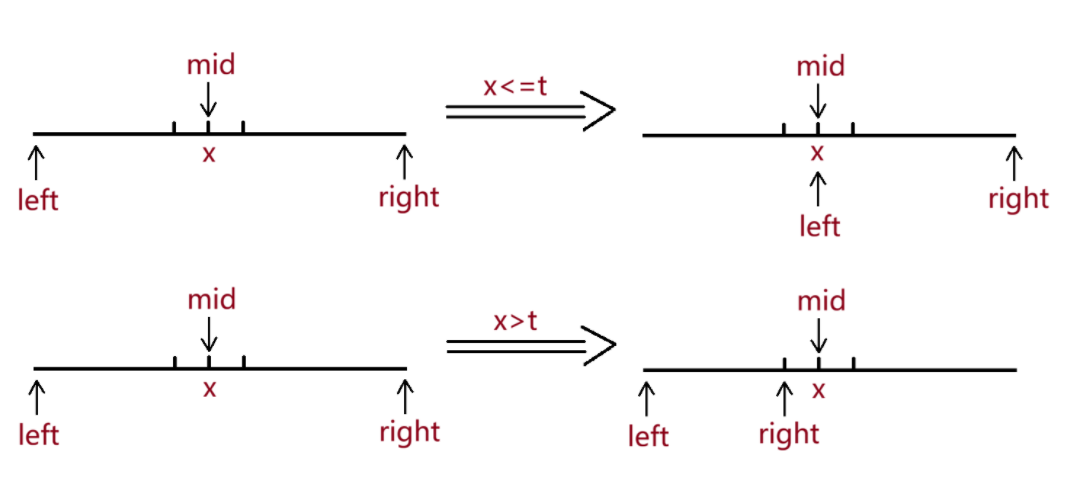
当x<=target时,将left移至mid
当x>target时,将right移至mid-1
循环条件:left<right
求中点的操作:left+(right-left+1)/2
当为left+(right-left)/2时,
,若x<=t,进入死循环,若x>t,left==right,退出循环。不符合要求。
当为left+(right-left+1)/2时,
,若x<=t,left==mid==right,退出循环。若x>t,left==mid==right,退出循环。符合要求。
代码如下:
cpp
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target)
{
if(nums.size()==0)
{
return {-1,-1};
}
int right=nums.size()-1,left=0,mid=0;
int begin=0,end=0;
vector<int> ret;
while(left<right)
{
mid=left+(right-left)/2;
if(nums[mid]<target)
{
left=mid+1;
}
else
right=mid;
}
if(nums[left]==target)
{
begin=left;
}
else
{
return {-1,-1};
}
right=nums.size()-1;
left=0;//或直接不修改,left可以从begin开始
while(left<right)
{
mid=left+(right-left+1)/2;
if(nums[mid]<=target)
{
left=mid;
}
else
right=mid-1;
}
if(nums[left]==target)
{
end=left;
}
return {begin,end};
}
};二分模板:
++查找区间左端点:++
cpp
while(left<right)
{
int mid=left+(right-left)/2;
if(......)left=mid+1;
else right=mid;
}++查找区间右端点:++
cpp
while(left<right)
{
int mid=left+(right-left+1)/2;
if(......)left=mid;
else right=mid-1;
}3.搜索插入位置

有了上一题的总结,这道题并不难,只需要划分<=target和>target的界限即可
需要注意的细节:如果target要插入在数组中或数组之前,只需返回left即可,如果要插入在数组之后则需返回left+1
代码如下:
cpp
class Solution {
public:
int searchInsert(vector<int>& nums, int target)
{
int left=0,right=nums.size()-1;
while(left<right)
{
int mid=left+(right-left+1)/2;
if(nums[mid]<=target)
{
left=mid;
}
else
{
right=mid-1;
}
}
if(nums[left]<target)
{
return left+1;
}
else
return left;
}
};4.x的平方根

也不难,只需要划分mid*mid<=x和>x的界限即可,若x==0,直接返回0
代码如下:
cpp
class Solution {
public:
int mySqrt(int x)
{
if(x==0)
{
return 0;
}
int left=1,right=x;
while(left<right)
{
long long mid=left+(right-left+1)/2;//注意溢出问题left不能等于0,否则right+1会溢出
if(mid*mid<=x)
{
left=mid;
}
else
right=mid-1;
}
return left;
}
};5.山脉数组的峰顶索引

区分单调递增和单调递减的界限即可
代码如下:
cpp
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr)
{
int left=1,right=arr.size()-2;//由于数组头尾元素不可能是山顶元素,所以left和right可以各向内一步开始
while(left<right)
{
int mid=left+(right-left+1)/2;
if(arr[mid]-arr[mid-1]>0)
{
left=mid;
}
else
right=mid-1;
}
return left;
}
};6.寻找峰值

这道题的二段性有点难找,但找到了代码就很简单
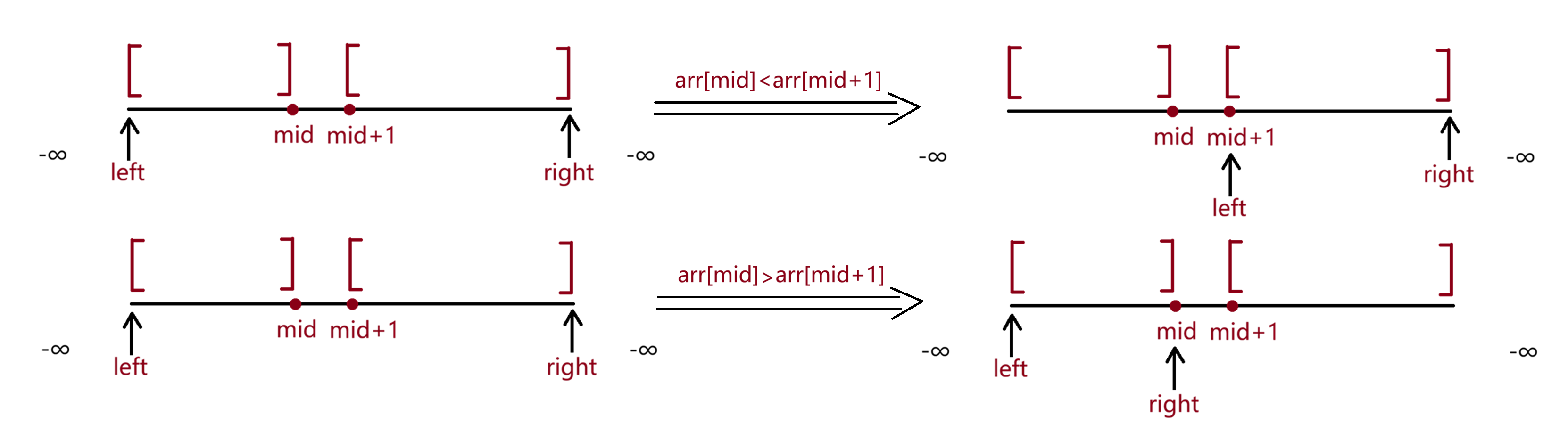
arr[mid]<arr[mid+1],那么左边的区间可能有峰值,右边的区间必定有峰值,到右边去找,left=mid+1
arr[mid]>arr[mid+1],那么左边的区间必定有峰值,右边的区间可能有峰值,到右边去找,right=mid
代码如下:
cpp
class Solution {
public:
int findPeakElement(vector<int>& nums)
{
int left=0,right=nums.size()-1;
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid]<nums[mid+1])
{
left=mid+1;
}
else
right=mid;
}
return left;
}
};7.寻找旋转排序数组中的最小值
153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)

这里的重难点也是要找到二段性,旋转数组可以分成两段:

A~B:nums[mid]>nums[n-1],left=mid+1
C~D:nums[mid]<=nums[n-1],right=mid
代码如下:
cpp
class Solution {
public:
int findMin(vector<int>& nums)
{
int left=0,n=nums.size(),right=n-1;
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid]<=nums[n-1])
{
right=mid;
}
else
left=mid+1;
}
return nums[right];
}
};以上是以D点为分界依据的情况,若换成以A点为分界依据呢?理论上也是可行的,但是还需要一些额外的细节处理:
cpp
class Solution {
public:
int findMin(vector<int>& nums)
{
int left=0,n=nums.size(),right=n-1;
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid]>=nums[0])
{
left=mid+1;
}
else
right=mid;
}
if(nums[right]>nums[0])
{
return nums[0];
}
return nums[right];
}
};如果以A为分界依据,一旦数组严格升序排列就会找到最大值,需要最后判断一下。
8.点名

这道题的方法有很多:哈希表、直接遍历、位运算、数学(高斯求和),但二分算法更优。
这道题找二段性的角度也很独特:

注意一个细节:如果数组是严格升序的(无空位),那么说明缺席同学在数组尾端后一个
代码如下:
cpp
class Solution {
public:
int takeAttendance(vector<int>& records)
{
int left=0,right=records.size()-1;
while(left<right)
{
int mid=left+(right-left)/2;
if(mid==records[mid])
{
left=mid+1;
}
else
right=mid;
}
if(left==records[left])
{
return records[left]+1;
}
return records[left]-1;
}
};