【优选算法・双指针】以 O (n) 复杂度重构数组操作：从暴力遍历到线性高效的范式跃迁

前言

注意注意！"双指针" 这货其实是个 "冒牌货"------ 根本不是真・指针，纯靠数组下标 cosplay 俩指针在那跑来跑去～但别小看这操作，本来得嵌套循环累到 O (n²) 的题，它俩一溜达就能给干到 O (n)，主打一个 "花最少的力气办最大的事"。下面这些题，就是这俩 "戏精下标" 的高光时刻～

1、移动零

[☆ 算法原理](#☆ 算法原理)

2、复写零

[☆ 算法原理](#☆ 算法原理)

3、快乐数

[☆ 算法原理](#☆ 算法原理)

4、盛水最多的容器

[☆ 算法原理](#☆ 算法原理)

[5、有效三角形的个数](#5、有效三角形的个数)

[☆ 算法原理](#☆ 算法原理)

[LCR 179. 查找总价格为目标值的两个商品](#LCR 179. 查找总价格为目标值的两个商品)

[☆ 算法原理](#☆ 算法原理)

7、三数之和

[☆ 算法解析](#☆ 算法解析)

8、四数之和

[☆ 算法原理](#☆ 算法原理)

1、移动零

【题目链接】 ：https://leetcode.cn/problems/move-zeroes/description/

☆ 算法原理

这类问题可以分为数组划分或者叫数组分块，并且使用双指针算法。

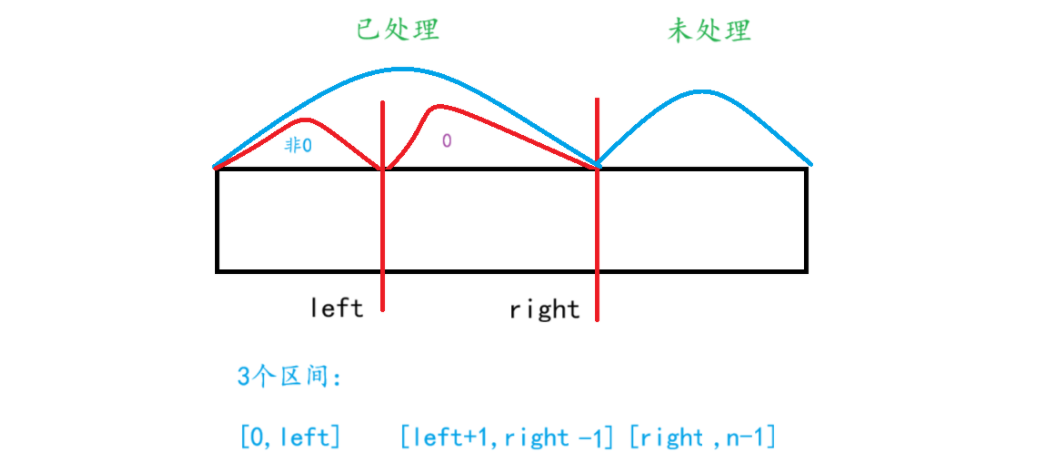
1、指针作用：

**[left] :**始终指向已处理区间内的最后一个非0元素处

[right]: 从左到右依次遍历数组

2、具体步骤：

1、利用right从左到右依次遍历的过程中：

2、【遇到非0元素】：left++，交换left和right处的元素， right++

3、【遇到0】：right++

3、只要保证left始终在最后一个非0元素的位置，right从左往右遍历即可

【代码演示】：

cpp 复制代码

class Solution
 {
public:
    void moveZeroes(vector<int>& nums) 
    {
        for(int right = 0, left = -1; right < nums.size(); right++)
        {
            if(nums[right]) 
               swap(nums[right],nums[++left]);
        }
    }
};

2、复写零

【题目链接】： https://leetcode.cn/problems/duplicate-zeros/

☆ 算法原理

最初尝试解决这道题时，我首先考虑从前往后遍历 数组：遇到非零元素就继续后移，遇到 0 就进行复写（添加一个 0）。但在画图模拟时发现，这种方式会覆盖还未进行操作的有效元素（因为复写 0 会占用额外位置，导致后续元素被提前覆盖），所以从前往后的算法思路不可行。

随后我转向从后往前遍历 的思路，但直接从后往前遍历难以精准控制元素的复写与位移。于是我想到：可以先找到最后一个需要参与复写的元素的位置，再基于这个位置从后往前进行复写操作，这样能避免元素覆盖问题，且更容易控制流程。

1、先找最后一个复写元素的位置

2、我们这时候得考虑个特殊情况，如果最后一个复写的元素是0，但是只有一个有效位置了，这时候dest就等于n了，我们只需要进行边界判断即可解决这种情况

3、从后往前完成复写操作

【演示代码】：

cpp 复制代码

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        //先找最后一个复写0的位置
        int cur = 0,dest = -1,n = arr.size();
        while(dest<n)
        {
            if(arr[cur])
                dest++;
            else
                dest+=2;
            //当dest等于n-1时，cur指向最后一个要复写的元素，
            //dest大于n-1代表，最后一个要复写的元素是0，但是只有一个有效位置了
            if(dest>=n-1)
            break;

            cur++;
        }

        //处理边界
        if(dest == n)
        {
            arr[n-1] = 0;
            cur--;
            dest-=2;
        }

        //从后往前完成复写
        while(cur>=0)
        {
            arr[dest--] = arr[cur];
            if(arr[cur]==0)
            {
                arr[dest--] = 0;

            }
            
            cur--;
        }
    }
};

3、快乐数

【题目链接】： https://leetcode.cn/problems/happy-number/description/

☆ 算法原理

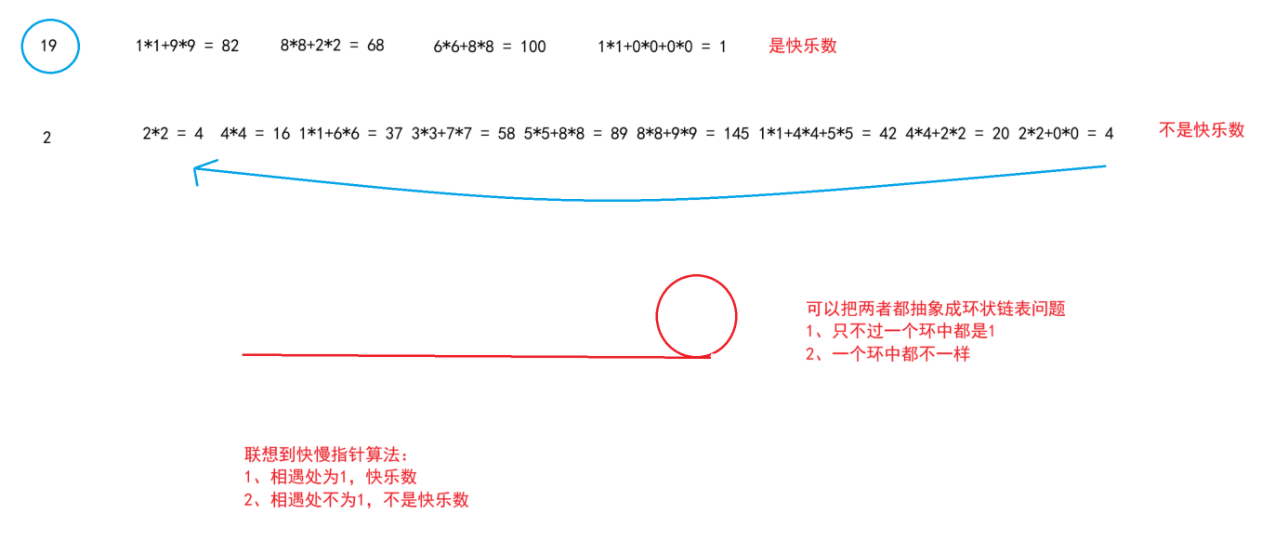
所以我们可以定义两个下标分别标识快指针 和慢指针，快指针一次走两步，慢指针一次走一步，由于他俩每走一步，之间的距离缩减1，那么他们肯定会在环中相遇

【代码示例】：

cpp 复制代码

class Solution {
public:
    // 计算一个数各位数字的平方和
    int qdsum(int n)
    {   
        int sum = 0;   
        while(n)    
        {
           int i = n%10;   
           sum += i*i;     
           n /=10;    
        }     
        return sum;   
    }


    bool isHappy(int n) {
     int slow = n;  // 慢指针：初始值为n，每次计算1次平方和（走1步）
     int fast = qdsum(n);  // 快指针：初始值为n的第一次平方和，每次计算2次平方和（走2步）

     //没相遇就一直走
     while (slow != fast)
     {
         slow = qdsum(slow);  // 慢指针走1步：计算当前值的平方和
         fast = qdsum(qdsum(fast));  // 快指针走2步：连续计算两次平方和
     }

     // 当快慢指针相遇时，若值为1则是快乐数，否则陷入非1的循环，不是快乐数
     if (slow == 1)
         return true;
     else
         return false;
 }
};

4、盛水最多的容器

【题目链接】：https://leetcode.cn/problems/container-with-most-water/

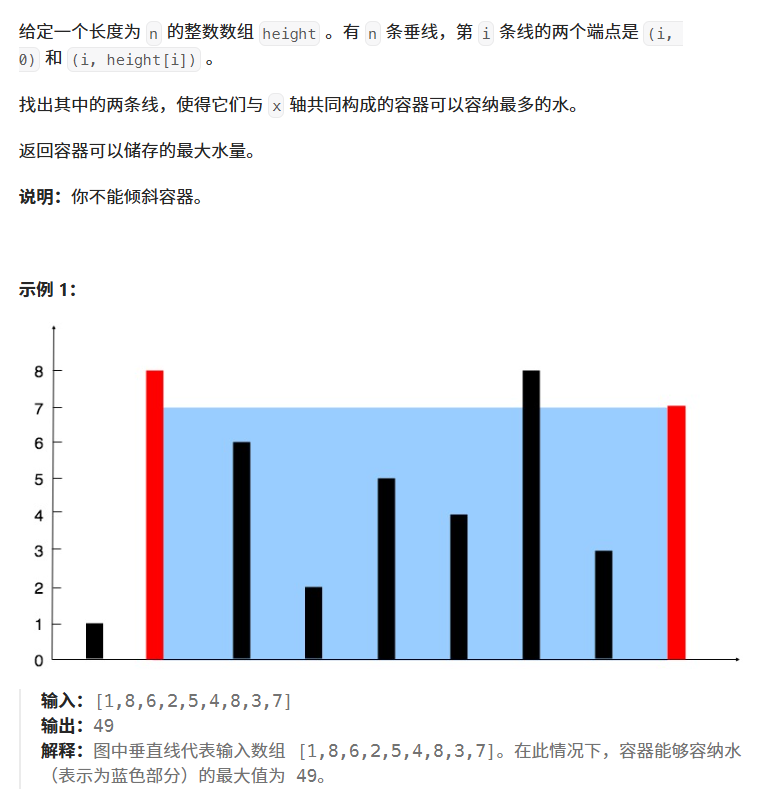
☆ 算法原理

思路1：暴力枚举（会超时）

固定第一个数，让第一个数和其后面的所有数进行穷举，然后每次刷新较大值，然后固定第二个数，以此类推......

【代码示例】：

cpp 复制代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0;
        int ret = 0;
        while(left < height.size())
        {    
             //right每次都从left的下一个位置开始穷举
             int right = left +1;
             while(right < height.size())
             {
                  int v = (right - left) * min(height[left],height[right]);
                  ret = max(v,ret);

                  right++;
             }

             left++;
        }

        return ret;
    }
};

思路2：双指针

cpp 复制代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0,right = height.size()-1,ret = 0;

        while(left < right)
        {
              int v = min(height[left],height[right]) * (right - left);
              ret = max(v,ret);

              if(height[left]>height[right])
              {
                 right--;
              }
              else
              {
                left++;
              }
        }

        return ret;
    }
};

5、有效三角形的个数

【题目链接】：https://leetcode.cn/problems/valid-triangle-number/

☆ 算法原理

思路1：暴力求解（会超时）

3层for循环，时间复杂度是O(N^3),超时了

cpp 复制代码

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
         int count = 0;
         for(int i = 0;i<nums.size();i++)
         {
            for(int j = i+1;j<nums.size();j++)
            {
                for(int k = j+1;k<nums.size();k++)
                {
                    if(nums[i]+nums[j]>nums[k] && nums[i]+nums[k]>nums[j] && nums[j]+nums[k]>nums[i])
                    {
                        count++; 
                    }
                }
            }
         }


         return count;
    }
};

思路2：双指针优化

cpp 复制代码

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        int count = 0;
        sort(nums.begin(), nums.end()); // 排序：为双指针优化做准备
        
        // 固定最大边nums[n]，从后往前遍历（n至少为2，需3条边）
        for(int n = nums.size() - 1; n >= 2; n--) {
            int left = 0, right = n - 1; // 双指针：在[0, n-1]中找两条较小边
            while(left < right) {
                // 若当前两边和>最大边，说明left到right-1的所有边与right组合均满足条件
                if(nums[left] + nums[right] > nums[n]) {
                    count += (right - left); // 直接统计right-left个有效组合
                    right--; // 缩小右指针，继续判断更小的right
                } else {
                    left++; // 两边和不足，增大左指针尝试更大值
                }
            }
        }
        return count;
    }
};

时间复杂度从O(N^2) 优化到了O**(N*logn + N^2)**

LCR 179. 查找总价格为目标值的两个商品

【题目链接】：https://leetcode.cn/problems/he-wei-sde-liang-ge-shu-zi-lcof/description/

☆ 算法原理

思路1：暴力枚举（会超时）

cpp 复制代码

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        for(int i = 0;i<price.size();i++)
        {
            for(int j = i+1;j<price.size();j++)
            {
                int sum = price[i] + price[j];
                if(sum == target)
                {
                    return {price[i],price[j]};
                }
            }
        }

        return {-1,-1};
    }
};

思路2：双指针优化

相较于暴力求解的O(N^2)，通过单调性和双指针最坏只用遍历一遍数组就可以解决

cpp 复制代码

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        int left = 0;
        int right = price.size() - 1;
        for(int i = 0;i<price.size();i++)
        {
            int sum = price[left] + price[right];
            if(sum > target)
            {
                right--;
            }
            else if(sum < target)
            {
                left++;
            }
            else
            {
                // 列表初始化返回值：用大括号{}直接构造vector<int>，包含找到的两个数值
                return {price[left], price[right]};
            }
        }

        // 列表初始化返回值：构造包含{-1,-1}的vector<int>，作为未找到时的默认返回
        return {-1, -1};
    }
};

7、三数之和

【题目】： https://leetcode.cn/problems/3sum/description/

☆ 算法解析

思路一：暴力求解（超时）

cpp 复制代码

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
    sort(nums.begin(), nums.end());
    vector<vector<int>> vv;
    int n = nums.size();
    for(int i = 0;i<n;i++)
    {
        // 去重i：如果当前i和前一个i元素相同，跳过（避免重复枚举同一i对应的组合）
        if (i > 0 && nums[i] == nums[i-1]) continue;

        for(int j = i+1;j<n;j++)
        {

            // 保留当前层的第一个元素，只跳过后续的重复元素
            // 去重j：如果当前j和前一个j元素相同，跳过
            if (j > i + 1 && nums[j] == nums[j-1]) continue;

            for(int k = j+1;k<n;k++)
            {
                 // 去重k：如果当前k和前一个k元素相同，跳过
                if (k > j + 1 && nums[k] == nums[k-1]) continue;

                if(nums[i]+nums[j]+nums[k] == 0)
                {
                    vv.push_back({nums[i],nums[j],nums[k]});
                }

                
            }
        }
    }

    return vv;

   
    }
};

排序：为后面去重做准备；3层for循环嵌套，时间复杂度为O(N^3),超时了

思路二：双指针+单调性进行优化

cpp 复制代码

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
          //1、排序
          sort(nums.begin(),nums.end());
          
          //存放三元组的二维数组
          vector<vector<int>> vv;

          for(int i = 0; i<nums.size();i++)
          {   
              //如果数据大于0了就不用在后面匹配了，因为后面的都是正数，两个正数相加不可能为负数，也就不可能等于0了
              if(nums[i]>0)
              {
                  break;
              }
              
              // i不能提前去重，不然后面的left和right的匹配就会受到影响
              if(i > 0 && nums[i] == nums[i-1]) continue;
             
              //二元组下标
              int left = i+1;
              int right = nums.size()-1;
              
              //left<right就继续查找
              while(left < right)
              {

                
                        
                   //固定位置值的相反数
                   int sum = -nums[i];
                   if(left < right && nums[left] + nums[right] == sum)//存储最终结果 
                   {
                        //满足条件的三元组进行尾插
                        vv.push_back({nums[i],nums[left],nums[right]});

                    //left去重 
                    //left<right防止越界
                    left++;
                    while(left < right && nums[left] == nums[left-1])
                    {
                        left++;
                    }

                    //right去重 
                    //left<right防止越界
                    right--;
                    while(left < right && nums[right] == nums[right+1])
                    {
                        right--;
                    }  

                   }
                   //判断二元组的和和上一个题思路一样，我就不多注释了
                   else if(left < right && nums[left] + nums[right] > sum)
                   {
                         right--;
                   }
                   else
                   {
                         left++;

                   }
              }
          }


          return vv;
    }
};

由于数据预先进行了排序，所以去重直接和下一个位置比较即可

8、四数之和

【题目】： https://leetcode.cn/problems/4sum/description/

☆ 算法原理

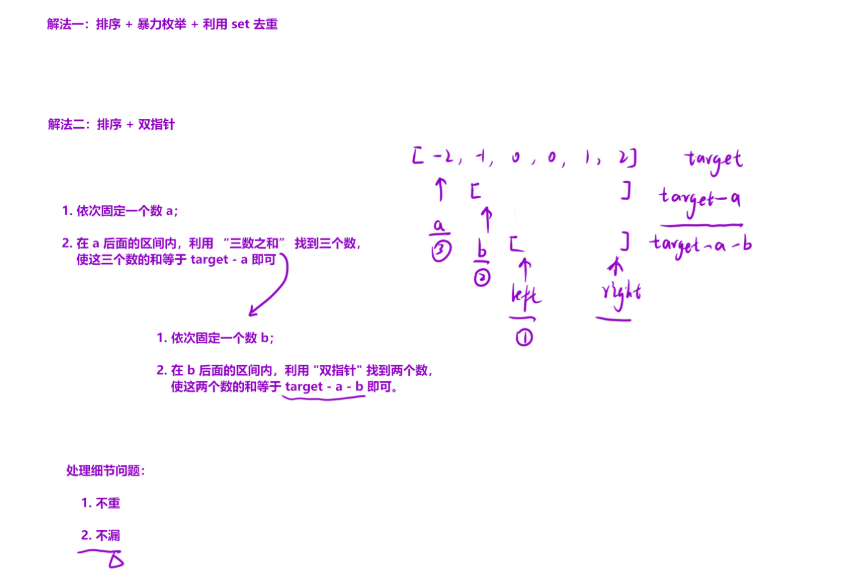
这道题和三数之和思路基本差不多，就是多固定了一个数。

思路一复杂度太高超时了，就直接写思路二的代码了

cpp 复制代码

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
         sort(nums.begin(),nums.end());
         vector<vector<int>> vv;

         int n = nums.size();
         for(int a =0; a < n; )//固定第一个数
         {
               for(int b = a+1; b < n ;)//固定第二个数
               {
                   //把target-a-b的值存起来，方便比较
                   //用longlong存储是因为，数值大点相减就超范围了
                   long long ami = (long long)target - nums[a] - nums[b];
                   
                   //left始终是固定的第二个数的下一个位置
                   int left = b+1;
                   int right = n-1;

                   while(left<right)
                   {

                        
                        int sum = nums[left] + nums[right];
                        
                        //利用单调性去掉不必要的枚举，上面几个题有同样的思路
                        if(sum > ami)
                        {
                            right--;
                        }
                        else if(sum < ami)
                        {
                            left++;
                        }
                        else
                        {
                            vv.push_back({nums[a],nums[b],nums[left++],nums[right--]});
                            
                            //left和right去重
                            while(left<right && nums[left] == nums[left-1])
                            {
                                left++;
                            }

                            while(left<right && nums[right] == nums[right+1])
                            {
                                right--;
                            }


                        }


                     
                   } 
                      //固定的第二个数去重
                        b++;
                        while(b < n && nums[b] == nums[b-1])
                        {
                            b++;
                        }

                   
                    
               }
                   //固定的第一个数去重
                        a++;
                        while(a < n && nums[a] == nums[a-1])
                        {
                            a++;
                        }


         }

         return vv;
    }
};

【优选算法・双指针】以 O (n) 复杂度重构数组操作：从暴力遍历到线性高效的范式跃迁

1、移动零

☆ 算法原理

2、复写零

☆ 算法原理

3、快乐数

☆ 算法原理

4、盛水最多的容器

☆ 算法原理

5、 有效三角形的个数

☆ 算法原理

LCR 179. 查找总价格为目标值的两个商品

☆ 算法原理

7、三数之和

☆ 算法解析

8、四数之和

☆ 算法原理

5、有效三角形的个数