《精准测量的起点：STM32中的电压电流有效值计算算法》

引言：当精度成为产品的生命线

面对电力仪表规格书上"0.5S级"的精度要求，你是否曾在算法选择上犹豫不决？网上充斥着基础的ADC教程，但能将理论转化为稳定工业产品的实战指南却凤毛麟角。

我曾深耕电力行业多年，主导过多款量产产品的完整开发。深谙"在精密测量领域，算法不仅是功能，更是产品的'良心'。"今天，我们不谈复杂的公式推导，聚焦于工程师最关心的三个核心问题：为什么必须用真有效值？如何在STM32中构建高可靠性的实现架构？调试时会遇到哪些真实的"坑"？

一、算法抉择：两种世界，两种结局

许多工程师为节省资源，会选择"绝对值平均法"。其逻辑简单：对采样值取绝对值后平均，再乘以一个固定的正弦波系数（约1.1107）。在实验室的纯净正弦波下，它看似完美。

然而，工业现场是算法的试金石。真实的电网充满变频器、整流设备等非线性负载，波形严重畸变。

一个决定性的对比测试

我们模拟一个典型工业场景：220V/50Hz基波叠加30%七次谐波（变频器常见谐波）。

算法	测得值 (V)	绝对误差 (V)	相对误差	是否满足 0.5S 级 (±0.5%)
真有效值 (True-RMS)	229.7	0.0	0.0%	✓ 完美满足
绝对值平均法	247.3	+17.6	+7.7%	✗ 严重超标 (超限值15倍)

这个+7.7%的误差意味着什么？ 对于一台工商业电表，这意味着每100度电会产生近7.7度的计量偏差，足以引发重大的财务纠纷和信任危机。

物理本质的差异：

绝对值平均法 ：其本质是对波形形状的一种近似 。它假设所有信号都是完美的正弦波，并用一个固定的系数来补偿。一旦波形畸变，这个模型就失效了，计算结果会系统性偏离真实的能量值。
真有效值 (True-RMS) ：其本质是能量等效的直接度量。它基于焦耳定律，通过"平方-平均-开方"的过程，对任何波形都严格成立。因此，真有效值算法不是"更好的近似"，而是"正确的答案"。

结论：在谐波普遍的工业电网中，选择真有效值算法不是技术偏好，而是保障计量公平、规避商业风险的底线。你的产品可靠性，从这第一个算法抉择开始奠基。

二、核心实现：一个稳定可靠的均方根计算模块如何构建？

在STM32中实现真有效值，核心公式就一行：

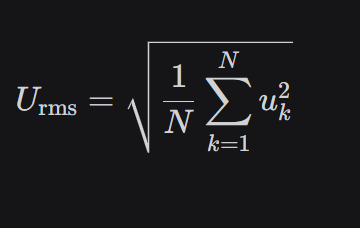
但将其转化为稳定、高效、可靠的产品级代码，则需要一套完整的工程架构。

我们推荐并采用 "ADC同步采样 + DMA双缓冲 + 信号预处理 + 滑动窗口实时更新" 的完整方案。

1. 硬件架构：为精度奠基

工业计量的精度始于硬件设计。我们的目标是：获取严格同步的电压电流采样点 ，并确保数据无丢失、无延迟地送入处理单元。

同步采样 ：利用STM32双ADC的"主从模式"，由一个精确定时器同时触发两个ADC的转换。这从硬件根源上保证了电压和电流的每一个采样点都在同一时刻被捕获，为后续的瞬时功率计算奠定了不可替代的物理基础。
DMA双缓冲 ：这是实现"零CPU干预、零数据丢失"的关键。DMA在后台自动搬运数据至两个交替的缓冲区（乒乓缓冲），当一块填满时触发中断通知CPU处理，同时DMA无缝切换到另一块继续填充。这确保了在高采样率下数据流的绝对连续与完整。

2. 软件架构：模块化与高效率

整个数据处理流程被设计为一个模块化、高效率的软件流水线，其核心数据流与架构如下图所示：

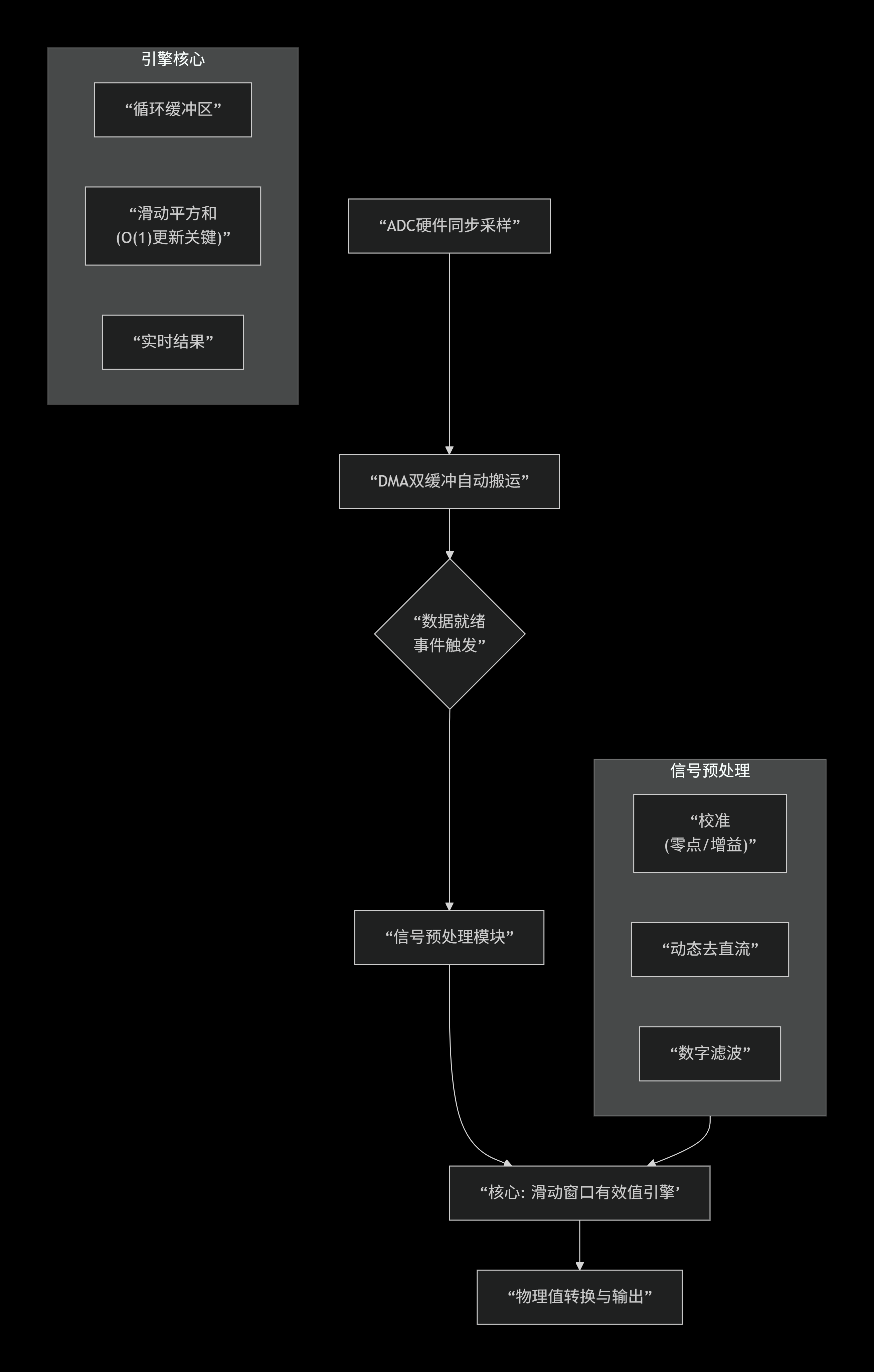
核心处理流程与设计思想：

① 信号预处理模块

该模块对原始ADC数据进行三道"精加工"，均在整型域进行以追求极致效率：

校准：应用出厂标定的硬件零点偏移Offset系数，将原始ADC值进行零点校准。
动态去直流 ：
数字滤波：对小批量数据执行中值滤波（如5点窗口），在源头有效抑制工业现场的偶发脉冲干扰，且计算开销可控。

② 滑动窗口有效值计算引擎（算法核心）

这是实现连续、实时、高效输出的灵魂所在。我们摒弃了每次都对整个历史窗口（如800点）进行重新遍历（O(N)复杂度）的传统方法，设计了独特的O(1)更新算法。

设计核心 ：维护一个长度为N的循环缓冲区 和一个对应的滑动平方和变量。
更新魔法：当一个新的采样点到来时，算法仅需三步：
1. 从滑动平方和 中减去即将被覆盖的最旧点的平方。
2. 将新点的平方加入滑动平方和。
3. 用新点覆盖缓冲区中的最旧点，并移动索引。
巨大优势 ：无论历史窗口N有多大（800点或8000点），单次更新的计算量恒定且极少 （仅几次加减乘除）。这使得系统能够以极低的CPU开销，在任何时刻都提供基于最新N个连续采样点的、稳定且平滑的有效值结果，完美满足工业仪表对输出信号质量的苛刻要求。

③ 输出模块

从引擎中获取最新的平方均值，进行一次开方运算，并乘以最终的标度系数，即可输出高精度的电压、电流真有效值物理量。

3. 关键数据结构与接口设计（概念层）

为清晰展示架构而不涉及具体实现细节，其设计概念如下：

复制代码

// 计算器状态结构体（概念示例）
typedef struct {
    // 核心状态：
    // - 循环缓冲区 (存储近期历史样本)
    // - 滑动平方和 (64位，防止溢出)
    // - 窗口索引与有效计数
    // - 当前计算结果缓存
} rms_calculator_t;

// 核心接口（功能描述）:
// 初始化，设定窗口大小等参数
void rms_init(rms_calculator_t *ctx, int window_size);
// 核心更新：传入一个新样本，内部以O(1)复杂度更新状态
void rms_update(rms_calculator_t *ctx, int32_t new_sample);
// 获取结果：立即返回当前窗口下的有效值
float rms_get_value(rms_calculator_t *ctx);

三、调试心法：从正确算法到精确测量

当代码逻辑无误，但精度依然不达标时，请化身"电路侦探"，按照以下优先级系统排查：

第一站：直击源头------硬件信号链

基准是否稳固？ 用示波器检查STM32的VDDA/VERF引脚纹波（应<10mV）。这是ADC的"尺子"，其稳定性是精度的天花板。
采样是否精准？ 确认ADC由定时器触发，而非软件启动。用示波器观察采样触发信号，确保间隔绝对均匀，无"抖动"。
布局是否洁净？ 重点检查：模拟地与数字地是否单点连接 ？电流采样回路是否短而粗，远离开关电源和晶振？

第二站：审视自身------软件校准与滤波

校准是否到位？ "两点校准"是出厂必修课。零点（短路输入）与增益（施加标准源）系数必须精确测定并存储于非易失存储器。
参数是否合理？ 有效值计算窗口长度是否正好是工频周期的整数倍？若非整倍数，会因"频谱泄漏"导致结果持续波动。

结语：从公式到产品的距离

实现一个数学上的真有效值函数，或许只需一个下午。但打造一个能在-40℃到85℃、复杂电磁环境、十年生命周期内稳定可靠的工业级计量模块，则需要跨越从理论到工程的全部鸿沟。

这恰恰是嵌入式工程师的核心价值：以物理原理和标准为基石，用同步硬件保证数据真实，以高效算法确保实时连续，借系统校准达成绝对精度，并通过严谨的调试闭环解决所有不确定性。这条路没有捷径，唯有对原理的深究、对细节的苛求，以及无数次调试台中深夜的灯火。