105. 从前序与中序遍历序列构造二叉树

中等

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历 ， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

复制代码

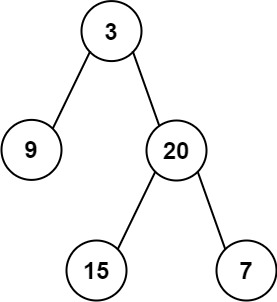
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

复制代码

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

📝 核心笔记：从前序与中序遍历构造二叉树 (Construct Tree from Preorder & Inorder)

1. 核心思想 (一句话总结)

"前序定根，中序分左右。"

前序遍历 ( Root -> Left -> Right**)** ：告诉我们谁是根节点（永远是第一个元素）。
中序遍历 ( Left -> Root -> Right**)** ：告诉我们左右子树有多大（找到根节点的位置，左边就是左子树，右边就是右子树）。
利用这个性质，我们可以把数组"切"成两半，递归地去构建左子树和右子树。

2. 算法流程 (分治切割)

找根 (Locate Root)：

- rootVal = preorder[0]。

算大小 (Calculate Size)：

- 去 inorder 数组里找到 rootVal 的下标 i。
- leftSize = i - 0（中序数组中，根节点左边的元素个数）。

切数组 (Slice & Recurse)：

- 左子树：

- - 前序：[1, 1 + leftSize]
  - 中序：[0, leftSize]

- 右子树：

- - 前序：[1 + leftSize, end]
  - 中序：[leftSize + 1, end]

连接 (Link) ：root.left = recurse(...), root.right = recurse(...)。

3. ⚠️ 性能优化的进阶 (面试必考)

您的写法虽然逻辑完美，但存在两个性能瓶颈：

时间：indexOf 每次都是 $O(N)$ 扫描，总复杂度退化为 $O(N\^2)$ 。
空间：Arrays.copyOfRange 每次都开辟新数组，空间消耗巨大。

优化方案：

哈希表优化 ：一开始把 inorder 的元素和下标存入 HashMap，实现找根。
指针优化 ：不切数组，而是传递 下标范围 (preStart, preEnd, inStart, inEnd)。

🔍 代码回忆清单

复制代码

// 题目：LC 105. Construct Binary Tree from Preorder and Inorder Traversal
class Solution {
    // 缓存中序遍历的 (值 -> 下标)，加速定位
    private Map<Integer, Integer> indexMap;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        indexMap = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) {
            indexMap.put(inorder[i], i);
        }
        // 传递数组范围，而不是拷贝数组
        return build(preorder, 0, preorder.length - 1, 
                     inorder, 0, inorder.length - 1);
    }

    private TreeNode build(int[] preorder, int preStart, int preEnd, 
                           int[] inorder, int inStart, int inEnd) {
        // 1. Base Case: 范围无效 (左指针跑过右指针)
        if (preStart > preEnd) {
            return null;
        }

        // 2. 找根节点值
        int rootVal = preorder[preStart];
        TreeNode root = new TreeNode(rootVal);

        // 3. 找根在中序中的位置 (O(1) 查表)
        int inRootIndex = indexMap.get(rootVal);
        
        // 4. 计算左子树的节点数量
        int leftSize = inRootIndex - inStart;

        // 5. 递归构建 (最容易写错下标的地方，建议画图)
        
        // 左子树：
        // Pre: [preStart + 1, preStart + leftSize] (根后面紧接着就是左子树)
        // In:  [inStart, inRootIndex - 1] (根左边全是左子树)
        root.left = build(preorder, preStart + 1, preStart + leftSize, 
                          inorder, inStart, inRootIndex - 1);

        // 右子树：
        // Pre: [preStart + leftSize + 1, preEnd] (剩下的部分)
        // In:  [inRootIndex + 1, inEnd] (根右边全是右子树)
        root.right = build(preorder, preStart + leftSize + 1, preEnd, 
                           inorder, inRootIndex + 1, inEnd);

        return root;
    }
}

⚡ 快速复习 CheckList (易错点)

为什么前序数组也要维护 start****和 end**？**

- 虽然我们只用 preorder[preStart] 找根，但在递归右子树时，我们需要计算右子树在前序数组中的起始位置（也就是跳过左子树那一段）。

下标偏移量怎么算？

- 左子树的前序结束位置 ：preStart + leftSize。
- 右子树的前序起始位置 ：preStart + leftSize + 1。
- 这个公式一定要理解记忆，死记硬背容易忘。

如果有重复元素怎么办？

- 题目通常保证树中没有重复元素。如果有，结果不唯一，或者需要更多信息。

🖼️ 数字演练

Pre: [3, 9, 20, 15, 7]

In: [9, 3, 15, 20, 7]

Level 1:

- Root = 3 (pre[0]).
- Inorder Index of 3 = 1.
- Left Size = 1 - 0 = 1.
- Left Recurse : Pre [9], In [9]. -> Returns Node(9).
- Right Recurse : Pre [20, 15, 7], In [15, 20, 7].

Level 2 (Right):

- Root = 20.
- Inorder Index of 20 = 3.
- Left Size (of 20) = 3 - 2 = 1 (元素 15).
- Left Recurse : Pre [15], In [15]. -> Returns Node(15).
- Right Recurse : Pre [7], In [7]. -> Returns Node(7).