22. 括号生成
python
class Solution(object):
def generateParenthesis(self, n):
"""
:type n: int
:rtype: List[str]
"""
# 只要left数目小于n,那么就可以继续加left
# 只要right数目小于left,那么就可以接续加right
res = []
def backtrack(path,left,right):
if len(path) == 2*n:
res.append(path)
if left<n:
backtrack(path+'(',left+1,right)
if right<left:
backtrack(path+')',left,right+1)
backtrack("",0,0)
return res79. 单词搜索
python
class Solution(object):
def exist(self, board, word):
"""
:type board: List[List[str]]
:type word: str
:rtype: bool
"""
# 图论+回溯
if not word:
return True
n,m = len(board),len(board[0])
visited = set()
dirs = [[1,0],[0,1],[-1,0],[0,-1]]
def backtrack(i,j,k):
if board[i][j] != word[k]:
return False
if k == len(word)-1:
return True
visited.add((i,j))
for di,dj in dirs:
newi,newj = i+di,j+dj
if 0<=newi<n and 0<=newj<m and (newi,newj) not in visited:
if backtrack(newi,newj,k+1):
return True
visited.remove((i,j))
return False
for i in range(n):
for j in range(m):
if backtrack(i,j,0):
return True
return False(i,j,k) 表示判断以网格的 (i,j) 位置出发,能否搜索到单词 word[k..],其中 word[k..] 表示字符串 word 从第 k 个字符开始的后缀子串。如果能搜索到,则返回 true,反之返回 false。
对每一个位置 (i,j) 都调用函数k(i,j,0) 进行检查:只要有一处返回 true,就说明网格中能够找到相应的单词。【visited是为了防重复】
时间复杂度:O(M*N*3^L) # M,N 为网格的长度与宽度,L 为字符串 word 的长度。这是一个宽松上界,除了第一次可以进入 4 个分支以外,其余时间最多会进入 3 个分支(每个位置只能使用一次,所以走来的分支没法走回)。由于单词长为 L,所以是3^L,要执行 O(MN) 次检查。但是由于剪枝,所以实际时间复杂度远远小!
空间复杂度:O(MN) # O(MN) 的 visited 数组,栈的深度最大为 O(min(L,MN))。
131. 分割回文串
python
class Solution(object):
def isPalindrome(self,s,left,right):
while left<right:
if s[left]!=s[right]:
return False
left +=1
right -= 1
return True
def partition(self, s):
"""
:type s: str
:rtype: List[List[str]]
"""
res = []
path = []
n = len(s)
def backtrack(start):
if start>=n:
res.append(path[:])
return
for i in range(start,n):
if self.isPalindrome(s,start,i):
path.append(s[start:i+1])
else:
# 一旦有一个不是,整个path都得放弃
# 这条path的start永远不满足条件,不会被写入res
continue
backtrack(i+1)
path.pop()
backtrack(0)
return res时间复杂度:O(n⋅2^n ) # n 是字符串 s 的长度。在最坏情况下,s 包含 n 个完全相同的字符,任意一种划分方法都满足要求,划分方案数为 2^(n−1)=O(2^n),每一种划分方法需要 O(n) 的时间求出对应的划分结果并放入答案,总时间复杂度为 O(n⋅2^n)。
空间复杂度:O(n^2) # 回溯需要O(n) 的栈空间以及 O(n) 的用来存储当前分割方法的空间。
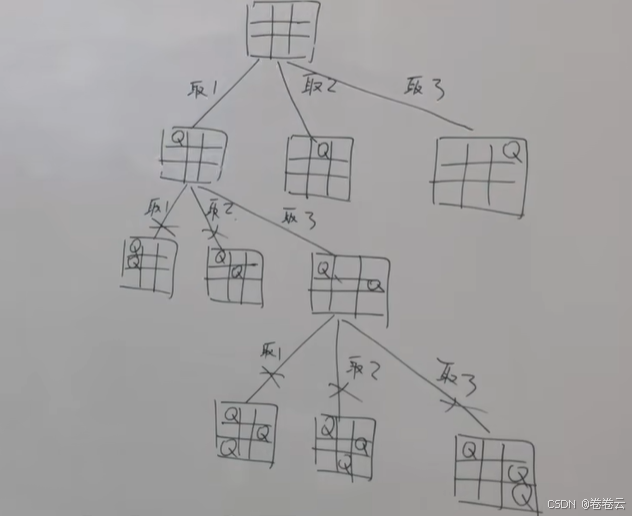
52. N皇后
python
class Solution(object):
def isValid(self,chessboard,x,y,n):
# 我们仅仅检查新加入的元素是否正确
# 当我们加入x行,仅仅检查0-(x-1)行
for i in range(0,x):
for j in range(n):
if j == y and chessboard[i][j] == 'Q':
return False
if abs(x-i) == abs(y-j) and chessboard[i][j] == 'Q':
return False
return True
def solveNQueens(self, n):
"""
:type n: int
:rtype: List[List[str]]
"""
chessboard = [['.' for _ in range(n)] for _ in range(n)]
res = []
def backtrack(row):
if row>=n:
res.append([''.join(r) for r in chessboard])
return
for j in range(n):
if self.isValid(chessboard,row,j,n):
chessboard[row][j] = 'Q'
backtrack(row+1)
chessboard[row][j] = '.'
backtrack(0)
return res这里的isValid判断太慢!利用集合优化:
python
class Solution(object):
def solveNQueens(self, n):
"""
:type n: int
:rtype: List[List[str]]
"""
chessboard = [['.']*n for _ in range(n)]
col_set = set() # 存占用列
diag1_set = set() # 存反对角线
# 从右上到左下方向的对角线,在这条线上,行号与列号的和 row + col 是一个常数。
diag2_set = set() # 存正对角线
# 从左上到右下方向的对角线,在这条线上,行号与列号的差 row - col 是一个常数。
res = []
def backtrack(row):
if row>=n:
res.append([''.join(r) for r in chessboard])
return
for j in range(n):
if j in col_set or (row+j) in diag1_set or (row-j) in diag2_set:
continue
chessboard[row][j] = 'Q'
col_set.add(j)
diag1_set.add(row+j)
diag2_set.add(row-j)
backtrack(row+1)
chessboard[row][j] = '.'
col_set.remove(j)
diag1_set.remove(row+j)
diag2_set.remove(row-j)
backtrack(0)
return res时间复杂度:O(N!) # 第一个有N个选择,第二个有N-1个选择【算上对角线甚至更少!】,我们会及时剪枝,所以是O(N!)
空间复杂度:O(N) # 递归仅仅是N行【集合也有一定的空间;但是还是O(N)】