124. 二叉树中的最大路径和

困难

二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

复制代码

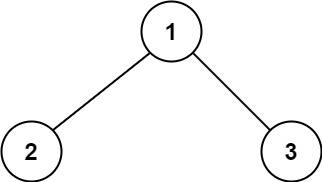
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

复制代码

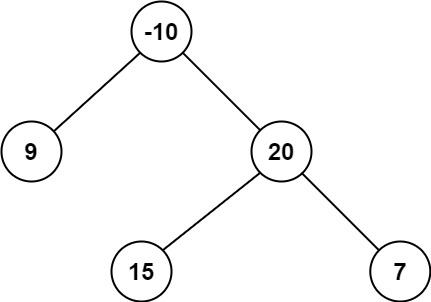
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000

📝 核心笔记：二叉树中的最大路径和 (Binary Tree Maximum Path Sum)

1. 核心思想 (一句话总结)

"每个人都有两个身份：在家里是'顶梁柱'（连接左右），在领导面前是'潜力股'（贡献单边）。"

这道题和 LC 543. 二叉树的直径 结构一模一样，区别在于：

直径：算边数，收益固定是 +1。
本题：算点权，收益可能是负数（需要贪心舍弃）。

2. 两个关键动作

对于任何一个节点 node，它要同时做两件事：

内部结算 (Update Global)：

- 尝试把 左边收益 + 自己 + 右边收益 连成一个"拱桥"。
- 用这个总和去挑战全局冠军 ans。
- 注：这条路径是"封顶"的，不能再往上延伸了。

向上汇报 (Return Value)：

- 只能选 (左边, 右边) 中收益大的那一支，加上自己，向上级汇报。
- 贪心时刻 ：如果我自己加上子树的结果是负数，那我还不如不干（返回 0）。这就相当于告诉父节点："别连我，连我会变小，把我当空气吧"。

🔍 代码回忆清单

复制代码

// 题目：LC 124. Binary Tree Maximum Path Sum
class Solution {
    private int ans = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        dfs(root);
        return ans;
    }

    // 函数定义：返回从当前节点向下延伸的【最大单边贡献值】
    // 如果贡献为负数，则返回 0 (相当于剪枝)
    private int dfs(TreeNode node) {
        if (node == null) {
            return 0;
        }

        // 1. 递归获取左右子树的贡献
        // 由于我们在 return 时做了 max(..., 0) 处理
        // 所以这里的 lVal 和 rVal 永远 >= 0
        int lVal = dfs(node.left); 
        int rVal = dfs(node.right); 

        // 2. 内部结算：挑战最大路径 (拐弯/拱桥)
        // 这一步计算的是"穿过当前节点"的最大路径
        ans = Math.max(ans, lVal + rVal + node.val); 

        // 3. 向上汇报：只能选一条路 (单边)
        // 核心贪心：如果 (max(左, 右) + 自己) < 0，那不如断尾求生，直接返回 0
        return Math.max(Math.max(lVal, rVal) + node.val, 0); 
    }
}

⚡ 快速复习 CheckList (易错点)

为什么要和 0 取最大值？

- 假设一个分支的路径和是 -10。如果父节点把这个分支连上，总分反而会减少。所以如果一个子树的贡献是负的，我们直接将其视为 0（断开连接）。

为什么 ans****更新要包含 lVal + rVal**，而返回只取** max**？**

- ans 是最终结果，路径可以从左子树上来，经过根，下到右子树（倒 V 字型），不需要继续向上延伸。
- return 是给父节点用的。父节点要连成线，只能接你的左手或者右手，不能让你劈叉。

全负数的情况？

- 如果树是 [-3]。
- dfs 内部：lVal=0, rVal=0。
- ans 更新为 -3。
- return 返回 0。
- 最终结果 -3。正确。

🖼️ 数字演练

树：[-10, 9, 20, 15, 7] (层序)

复制代码

Node 9: Left(0), Right(0).

- ans = 0+0+9 = 9.
- return 9.

Node 15: Left(0), Right(0).

- ans = max(9, 15) = 15.
- return 15.

Node 7: Left(0), Right(0).

- ans = max(15, 7) = 15.
- return 7.

Node 20:

- Receives: Left(15), Right(7).
- Internal: 15 + 7 + 20 = 42. ans = 42.
- Return: max(15, 7) + 20 = 35.

Node -10 (Root):

- Receives: Left(9), Right(35).
- Internal: 9 + 35 + (-10) = 34. ans 保持 42.
- Return: ... (doesn't matter).

Final Answer: 42.