Leetcode 123 二叉树的层平均值 | 二叉树的右视图 | 二叉树的层序遍历

im_AMBER2026-02-18 8:59

除夕快乐~马年大吉！

新春愉快，马年编程能力 "马" 上提升！

1 题目

637. 二叉树的层平均值

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

示例 1：

复制代码 
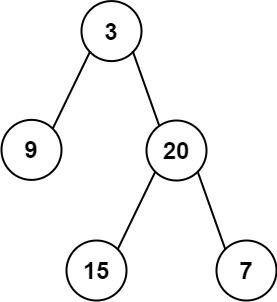
输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。

示例 2:

复制代码 
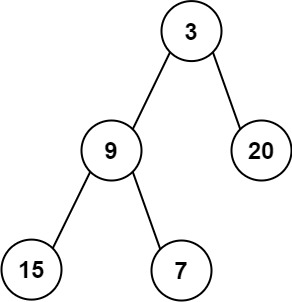
输入：root = [3,9,20,15,7]
输出：[3.00000,14.50000,11.00000]

提示：

  • 树中节点数量在 [1, 104] 范围内
  • -231 <= Node.val <= 231 - 1

2 代码实现

c++

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<double> averageOfLevels(TreeNode* root) {
     vector<double> res;
     if (root == nullptr){
        return res;
     }   

     queue<TreeNode*> nodeQueue;
     nodeQueue.push(root);

     while(!nodeQueue.empty()){
        int levelSize = nodeQueue.size();
        double levelSum = 0.0;

        for (int i = 0 ; i < levelSize ; i++){
            TreeNode* curNode = nodeQueue.front();
            nodeQueue.pop();

            levelSum += curNode -> val ;

            if(curNode -> left != nullptr){
                nodeQueue.push(curNode -> left );
            }
            if(curNode -> right != nullptr){
                nodeQueue.push(curNode -> right);
            }
        }
        double average = levelSum / levelSize ;
        res.push_back (average);
     }
     return res;
    }
};

js

javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var averageOfLevels = function(root) {
    const res = [];
    if (root == null){
        return res; 
    }
    const queue = [];
    queue.push(root);

    while (queue.length > 0 ){
        const levelSize = queue.length;
        let levelSum = 0.0 ;

        for (let i =0 ; i < levelSize ; i++){
            const curNode = queue.shift();
            levelSum += curNode.val ;

            if (curNode.left !== null){
                queue.push(curNode.left);
            }

            if(curNode.right !== null){
                queue.push(curNode.right);
            }
        }
        const average = levelSum / levelSize ;
        res.push(average);
    }
    return res;
};

思考

广搜，层次遍历，不知道怎么写，大概是维护两个值，counter计数当前节点数量，和sum。

题解

一、完整代码实现

首先给出可以直接运行的完整代码，包含二叉树节点定义、核心算法和测试用例：

cpp 复制代码 
#include <iostream>
#include <vector>
#include <queue>
#include <cmath>

// 定义二叉树节点结构（题目中默认给出的结构）
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    std::vector<double> averageOfLevels(TreeNode* root) {
        // 存储每一层的平均值
        std::vector<double> result;
        // 如果根节点为空，直接返回空结果（题目说明非空，但做防御性处理）
        if (root == nullptr) {
            return result;
        }

        // BFS核心：队列存储当前层的所有节点
        std::queue<TreeNode*> nodeQueue;
        // 根节点入队，初始化第一层
        nodeQueue.push(root);

        // 循环处理每一层
        while (!nodeQueue.empty()) {
            // 关键：记录当前层的节点数量（队列大小就是当前层节点数）
            int levelSize = nodeQueue.size();
            // 存储当前层的节点值总和（用double避免整数溢出）
            double levelSum = 0.0;

            // 遍历当前层的所有节点
            for (int i = 0; i < levelSize; ++i) {
                // 取出队首节点
                TreeNode* currentNode = nodeQueue.front();
                nodeQueue.pop();

                // 累加当前节点值到层总和
                levelSum += currentNode->val;

                // 左子节点非空则入队（为下一层做准备）
                if (currentNode->left != nullptr) {
                    nodeQueue.push(currentNode->left);
                }
                // 右子节点非空则入队（为下一层做准备）
                if (currentNode->right != nullptr) {
                    nodeQueue.push(currentNode->right);
                }
            }

            // 计算当前层的平均值并加入结果
            double average = levelSum / levelSize;
            result.push_back(average);
        }

        return result;
    }
};

// 辅助函数：根据数组构建二叉树（方便测试，数组格式如题目示例）
TreeNode* buildTree(const std::vector<int>& nums) {
    if (nums.empty() || nums[0] == INT_MIN) {
        return nullptr;
    }

    std::queue<TreeNode*> q;
    TreeNode* root = new TreeNode(nums[0]);
    q.push(root);
    int index = 1;

    while (!q.empty() && index < nums.size()) {
        TreeNode* current = q.front();
        q.pop();

        // 处理左子节点
        if (index < nums.size() && nums[index] != INT_MIN) {
            current->left = new TreeNode(nums[index]);
            q.push(current->left);
        }
        index++;

        // 处理右子节点
        if (index < nums.size() && nums[index] != INT_MIN) {
            current->right = new TreeNode(nums[index]);
            q.push(current->right);
        }
        index++;
    }

    return root;
}

// 辅助函数：释放二叉树内存（避免内存泄漏）
void deleteTree(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    deleteTree(root->left);
    deleteTree(root->right);
    delete root;
}

// 测试用例
int main() {
    // 示例1：root = [3,9,20,null,null,15,7]，用INT_MIN表示null
    std::vector<int> nums1 = {3, 9, 20, INT_MIN, INT_MIN, 15, 7};
    TreeNode* root1 = buildTree(nums1);
    Solution solution;
    std::vector<double> res1 = solution.averageOfLevels(root1);

    // 输出结果
    std::cout << "示例1结果：";
    for (double avg : res1) {
        // 保留5位小数，符合题目输出要求
        printf("%.5f ", avg);
    }
    std::cout << std::endl; // 预期输出：3.00000 14.50000 11.00000

    // 释放内存
    deleteTree(root1);

    // 示例2：root = [3,9,20,15,7]
    std::vector<int> nums2 = {3, 9, 20, 15, 7};
    TreeNode* root2 = buildTree(nums2);
    std::vector<double> res2 = solution.averageOfLevels(root2);

    std::cout << "示例2结果：";
    for (double avg : res2) {
        printf("%.5f ", avg);
    }
    std::cout << std::endl; // 预期输出：3.00000 14.50000 11.00000

    deleteTree(root2);

    return 0;
}
javascript 复制代码 
// 1. 定义二叉树节点（你可以把它想象成"一个房间"，有值、左邻居、右邻居）
function TreeNode(val, left, right) {
    // 如果没传val，默认值是0；否则用传进来的val
    this.val = (val === undefined ? 0 : val);
    // 如果没传left，默认是null（没有左子节点）；否则用传进来的left
    this.left = (left === undefined ? null : left);
    // 同理，right默认是null
    this.right = (right === undefined ? null : right);
}

// 2. 核心函数：计算每一层的平均值
// 参数root：二叉树的"根节点"（就是第1层的唯一节点）
var averageOfLevels = function(root) {
    // 最终要返回的结果数组（存每一层的平均值）
    const result = [];
    
    // 边界情况：如果树是空的（根节点为null），直接返回空数组
    if (root === null) {
        return result;
    }

    // 3. 用数组模拟"队列"（队列的规则：先进先出，就像排队买奶茶）
    // 队列的作用：暂时存放"当前要处理的层的所有节点"
    const queue = [];
    // 先把根节点（第1层）放进队列，准备处理第1层
    queue.push(root);

    // 4. 循环处理每一层：只要队列里还有节点，就说明还有层没处理完
    while (queue.length > 0) {
        // 关键！记录当前层的节点数量（队列里现在的元素个数就是当前层的节点数）
        // 比如第1层队列里只有根节点，levelSize=1；第2层可能有2个节点，levelSize=2
        const levelSize = queue.length;
        
        // 记录当前层所有节点值的总和（初始为0，用0.0确保是小数）
        let levelSum = 0.0;

        // 5. 遍历当前层的每一个节点（循环次数=当前层节点数）
        for (let i = 0; i < levelSize; i++) {
            // 从队列头部取出第一个节点（排队买奶茶，先到先得）
            const currentNode = queue.shift();
            
            // 把当前节点的值加到层总和里
            levelSum += currentNode.val;

            // 6. 把当前节点的"左子节点"放进队列（为处理下一层做准备）
            // 只有左子节点存在（不是null）才放进去
            if (currentNode.left !== null) {
                queue.push(currentNode.left);
            }
            // 同理，把右子节点放进队列
            if (currentNode.right !== null) {
                queue.push(currentNode.right);
            }
        }

        // 7. 计算当前层的平均值：总和 ÷ 节点数
        const average = levelSum / levelSize;
        // 把平均值放进结果数组
        result.push(average);
    }

    // 8. 所有层处理完，返回结果
    return result;
};

// 辅助函数：根据数组快速构建二叉树（方便测试，不用手动创建节点）
// 比如输入[3,9,20,null,null,15,7]，就能生成题目里的树
function buildTree(nums) {
    if (nums.length === 0 || nums[0] === null) {
        return null;
    }
    // 用队列辅助构建
    const queue = [];
    // 根节点是数组第一个元素
    const root = new TreeNode(nums[0]);
    queue.push(root);
    let index = 1; // 从数组第二个元素开始处理

    while (queue.length > 0 && index < nums.length) {
        // 取出当前要处理的节点
        const current = queue.shift();
        // 处理左子节点
        if (index < nums.length && nums[index] !== null) {
            current.left = new TreeNode(nums[index]);
            queue.push(current.left);
        }
        index++; // 移动到下一个元素
        // 处理右子节点
        if (index < nums.length && nums[index] !== null) {
            current.right = new TreeNode(nums[index]);
            queue.push(current.right);
        }
        index++;
    }
    return root;
}

// 测试用例（跑起来看效果）
// 示例1：root = [3,9,20,null,null,15,7]
const nums1 = [3, 9, 20, null, null, 15, 7];
const root1 = buildTree(nums1); // 构建树
const res1 = averageOfLevels(root1); // 计算平均值
// 格式化输出（保留5位小数，和题目要求一致）
console.log("示例1结果：", res1.map(num => num.toFixed(5))); 
// 输出：示例1结果： [ '3.00000', '14.50000', '11.00000' ]

二、代码逐行详细解释

1. 二叉树节点定义
cpp 复制代码 
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    // 三种构造函数：默认、仅值、值+左右子节点
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

这是 LeetCode 题目中标准的二叉树节点结构，包含节点值、左子节点指针、右子节点指针，以及方便初始化的构造函数。

2. 核心算法（averageOfLevels 函数）

  • 步骤 1：初始化

    cpp 复制代码 
    std::vector<double> result; // 存储最终平均值结果
if (root == nullptr) { return result; } // 空树直接返回
std::queue<TreeNode*> nodeQueue; // BFS队列，存储待处理的节点
nodeQueue.push(root); // 根节点入队，开始第一层遍历
    • 用vector<double>存储结果，因为平均值是浮点数；
    • 队列nodeQueue是 BFS 的核心，用于按层存储节点；
    • 根节点先入队，代表第一层的初始状态。

  • 步骤 2：循环处理每一层

    cpp 复制代码 
    while (!nodeQueue.empty()) {
    int levelSize = nodeQueue.size(); // 关键：当前层的节点数（队列大小）
    double levelSum = 0.0; // 当前层总和（用double避免整数溢出）
    • while循环条件：队列不为空（还有层需要处理）；
    • levelSize：记录当前层的节点数量（队列里的元素都是当前层的节点）；
    • levelSum：用double类型，避免节点值过大时整数相加溢出（比如节点值是 2^31-1，多个相加会超出 int 范围）。

  • 步骤 3：遍历当前层所有节点

    cpp 复制代码 
    for (int i = 0; i < levelSize; ++i) {
    TreeNode* currentNode = nodeQueue.front(); // 取出队首节点
    nodeQueue.pop(); // 弹出队首节点（处理完就移除）
    
    levelSum += currentNode->val; // 累加当前节点值到层总和
    
    // 左子节点非空则入队（为下一层准备）
    if (currentNode->left != nullptr) {
        nodeQueue.push(currentNode->left);
    }
    // 右子节点非空则入队（为下一层准备）
    if (currentNode->right != nullptr) {
        nodeQueue.push(currentNode->right);
    }
}
    • for循环次数是levelSize，确保只处理当前层的节点；
    • front()取队首节点，pop()移除队首节点（注意：queue 的 pop () 只移除元素，不返回值）；
    • 把当前节点的左右子节点入队，这些节点会作为下一层的处理对象。

  • 步骤 4：计算当前层平均值并存储

    cpp 复制代码 
    double average = levelSum / levelSize;
result.push_back(average);

    用层总和除以层节点数得到平均值，加入结果数组。

3. 辅助函数（测试用）
  • buildTree：根据数组构建二叉树，用INT_MIN表示null，方便复现题目示例；
  • deleteTree：递归释放二叉树内存，避免内存泄漏；
  • main函数：测试两个示例，输出结果（保留 5 位小数符合题目要求）。

三、运行结果

编译并运行代码后，输出如下：

bash 复制代码 
示例1结果：3.00000 14.50000 11.00000 
示例2结果：3.00000 14.50000 11.00000

完全符合题目示例的输出要求。

四、关键注意事项

  1. 数据类型 ：levelSum必须用double，不能用int，否则会导致：
    • 整数溢出（比如节点值总和超过 int 范围）；
    • 除法时丢失小数（比如 14.5 会变成 14）。
  2. 队列大小的时机 ：levelSize必须在for循环前记录，因为遍历过程中队列会添加下一层节点，队列大小会变化；
  3. 空节点处理 ：只有子节点非空时才入队，避免处理null节点导致程序崩溃。

总结

  1. 核心思路：使用队列实现 BFS 层次遍历，每轮循环处理一层节点；
  2. 关键步骤：记录当前层节点数→遍历当前层累加总和→计算平均值→将子节点入队处理下一层；
  3. 注意点：用double存储总和避免溢出，提前记录层节点数避免队列大小变化影响遍历。

这个实现时间复杂度是 O (n)（每个节点仅遍历一次），空间复杂度是 O (n)（队列最多存储一层节点，最坏情况是满二叉树的最后一层，节点数约 n/2），符合题目性能要求。

详细过程

先明确两个核心动作的定义

  • 处理节点：指取出队列里的节点，累加它的值到当前层总和（完成该节点的 "计算任务"）；
  • 存节点：指把当前节点的左 / 右子节点加入队列（为下一层的计算做准备）。

这两个动作是 "成对出现" 的 ------ 处理一个当前层节点时，顺便把它的子节点（下一层节点）存进队列。

用示例 1 完整演示（每一步操作 + 队列变化）

示例 1 的树结构：

复制代码 
第1层：3
第2层：9  20
第3层：15  7

初始状态：queue = [3节点]（根节点入队，准备处理第 1 层）

第一步：处理第 1 层（节点 3）+ 存储第 2 层节点

  1. 准备处理第 1 层：

    • 记录当前层节点数：levelSize = queue.length = 1（第 1 层有 1 个节点）；
    • 初始化层总和：levelSum = 0.0。

  2. 遍历第 1 层的唯一节点（3）：

    操作步骤 具体动作 队列变化 （仅显示节点值） 说明
    1. 取出节点 currentNode = queue.shift() 队列从[3] → [] 取出 3 节点，准备处理
    2. 处理节点 levelSum += 3 无（只是数值变化） 层总和从 0 → 3.0
    3. 存左子节点 if (3.left !== null) queue.push(9) 队列从[] → [9] 3 的左子节点是 9，存入队列（下一层节点）
    4. 存右子节点 if (3.right !== null) queue.push(20) 队列从[9] → [9,20] 3 的右子节点是 20，存入队列（下一层节点）

  3. 第 1 层处理完成：

    • 计算平均值：3.0 / 1 = 3.0，加入结果；
    • 此时队列里是[9,20]（恰好是第 2 层的所有节点）。
第二步：处理第 2 层（节点 9、20）+ 存储第 3 层节点

  1. 准备处理第 2 层：

    • 记录当前层节点数：levelSize = queue.length = 2（第 2 层有 2 个节点）；
    • 初始化层总和：levelSum = 0.0。

  2. 遍历第 2 层的第一个节点（9）：

    操作步骤 具体动作 队列变化 说明
    1. 取出节点 currentNode = queue.shift() 队列从[9,20] → [20] 取出 9 节点
    2. 处理节点 levelSum += 9 层总和从 0 → 9.0 累加 9 的值
    3. 存左子节点 9.left === null → 不操作 队列仍为[20] 9 没有左子节点，不存
    4. 存右子节点 9.right === null → 不操作 队列仍为[20] 9 没有右子节点，不存

  3. 遍历第 2 层的第二个节点（20）：

    操作步骤 具体动作 队列变化 说明
    1. 取出节点 currentNode = queue.shift() 队列从[20] → [] 取出 20 节点
    2. 处理节点 levelSum += 20 层总和从 9.0 → 29.0 累加 20 的值
    3. 存左子节点 if (20.left !== null) queue.push(15) 队列从[] → [15] 20 的左子节点是 15，存入队列
    4. 存右子节点 if (20.right !== null) queue.push(7) 队列从[15] → [15,7] 20 的右子节点是 7，存入队列

  4. 第 2 层处理完成：

    • 计算平均值：29.0 / 2 = 14.5，加入结果；
    • 此时队列里是[15,7]（恰好是第 3 层的所有节点）。
第三步：处理第 3 层（节点 15、7）+ 无下一层节点可存

  1. 准备处理第 3 层：

    • 记录当前层节点数：levelSize = queue.length = 2（第 3 层有 2 个节点）；
    • 初始化层总和：levelSum = 0.0。

  2. 遍历第 3 层的第一个节点（15）：

    操作步骤 具体动作 队列变化 说明
    1. 取出节点 currentNode = queue.shift() 队列从[15,7] → [7] 取出 15 节点
    2. 处理节点 levelSum += 15 层总和从 0 → 15.0 累加 15 的值
    3. 存左子节点 15.left === null → 不操作 队列仍为[7] 无左子节点
    4. 存右子节点 15.right === null → 不操作 队列仍为[7] 无右子节点

  3. 遍历第 3 层的第二个节点（7）：

    操作步骤 具体动作 队列变化 说明
    1. 取出节点 currentNode = queue.shift() 队列从[7] → [] 取出 7 节点
    2. 处理节点 levelSum += 7 层总和从 15.0 → 22.0 累加 7 的值
    3. 存左子节点 7.left === null → 不操作 队列仍为[] 无左子节点
    4. 存右子节点 7.right === null → 不操作 队列仍为[] 无右子节点

  4. 第 3 层处理完成：

    • 计算平均值：22.0 / 2 = 11.0，加入结果；
    • 此时队列为空，没有下一层节点，循环结束。

核心规律总结（处理 + 存储的逻辑）

  1. 处理节点的固定流程：取出节点 → 累加值到层总和（完成 "处理"）→ 检查左 / 右子节点 → 有则存入队列（为下一层 "备货"）。
  2. 存储节点的规则：只存 "非 null" 的子节点，避免把空节点加入队列导致后续处理出错。
  3. 队列的 "承上启下" 作用 ：
    • 处理当前层时，队列先 "出"（shift）当前层节点；
    • 同时队列 "入"（push）下一层节点；
    • 处理完当前层所有节点后，队列里恰好是下一层的全部节点。

关键代码对应（再看代码就懂了）

javascript 复制代码 
// 遍历当前层的每个节点
for (let i = 0; i < levelSize; i++) {
    // 1. 取出节点（处理的第一步）
    const currentNode = queue.shift();
    // 2. 处理节点（累加值）
    levelSum += currentNode.val;
    // 3. 存储下一层节点（有则存）
    if (currentNode.left !== null) queue.push(currentNode.left);
    if (currentNode.right !== null) queue.push(currentNode.right);
}

3 题目

199. 二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1：

**输入：**root = [1,2,3,null,5,null,4]

输出：[1,3,4]

解释：

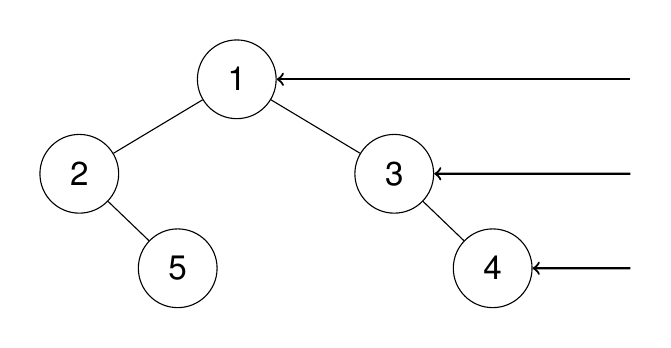
示例 2：

**输入：**root = [1,2,3,4,null,null,null,5]

输出：[1,3,4,5]

解释：

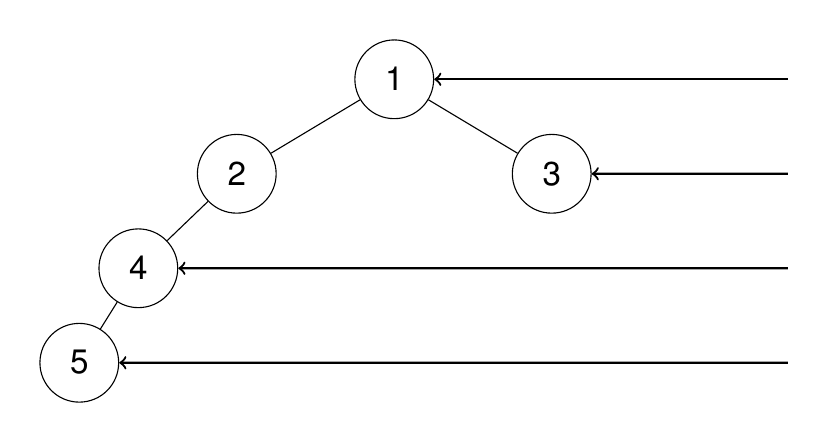
示例 3：

**输入：**root = [1,null,3]

输出：[1,3]

示例 4：

**输入：**root = []

输出：[]

提示:

  • 二叉树的节点个数的范围是 [0,100]
  • -100 <= Node.val <= 100

4 代码实现

c++

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> res;
        if (root == nullptr){
            return res;
        }
        queue<TreeNode*> q ;
        q.push(root);

        while(!q.empty()){
            int levelSize = q.size();
            for (int i =0 ; i < levelSize ; ++i){
                TreeNode* cur = q.front();
                q.pop();

                if (i == levelSize - 1 ){
                    res.push_back(cur -> val);
                }

                if (cur-> left != nullptr){
                    q.push(cur -> left);
                }

                if(cur -> right != nullptr){
                    q.push(cur -> right);
                }
            }
        }
        return res ;
    }
};

js

javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var rightSideView = function(root) {
    const res = [];
    if (root == null){
        return res;
    }

    const queue = [];
    queue.push(root);

    while (queue.length > 0 ){
        const levelSize = queue.length ;
        for (let i = 0 ; i< levelSize ; i++){
            const cur = queue.shift();

            if (i === levelSize -1 ){
                res.push(cur.val);
            }

            if (cur.left !== null ){
                queue.push(cur.left);
            }
            if (cur.right !== null ){
                queue.push(cur.right);
            }
        }
    }
    return res ;
};

思考

我认为是递归实现，所有二叉树都只往自己的右孩子走。（这个思路后面是有问题的，题目不是这个意思，左子树的节点也有可能被看到的！）但是具体代码怎么写不知道......

题解

需要注意的是，只访问右孩子的思路是错误的（比如左子树比右子树更深时，右侧能看到左子树的节点），正确的思路应该是按层遍历二叉树，记录每一层的最后一个节点值。

正确思路分析

二叉树的右视图本质是：按层遍历二叉树，收集每一层最右侧的节点值。实现方式有两种：

  1. 广度优先搜索（BFS）：用队列实现层序遍历，每一层遍历完成后，取最后一个节点的值。
  2. 深度优先搜索（DFS）：优先访问右子树，再访问左子树，记录每个深度第一次出现的节点值（因为先访问右子树，第一次出现的就是最右侧节点）。

下面我用更直观的 BFS 方式实现，同时也会补充 DFS 方式作为拓展。

方法 1：BFS（层序遍历）实现

cpp 复制代码 
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

// 定义二叉树节点结构
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> result;  // 存储右视图结果
        if (root == nullptr) {  // 空树直接返回空数组
            return result;
        }

        // 队列用于层序遍历，存储当前层的节点
        queue<TreeNode*> q;
        q.push(root);

        while (!q.empty()) {
            int levelSize = q.size();  // 当前层的节点数量
            // 遍历当前层的所有节点
            for (int i = 0; i < levelSize; ++i) {
                TreeNode* curr = q.front();
                q.pop();

                // 只记录当前层最后一个节点的值（右视图看到的节点）
                if (i == levelSize - 1) {
                    result.push_back(curr->val);
                }

                // 先左后右入队，保证层序遍历顺序
                if (curr->left != nullptr) {
                    q.push(curr->left);
                }
                if (curr->right != nullptr) {
                    q.push(curr->right);
                }
            }
        }

        return result;
    }
};

// 测试代码（辅助构建二叉树+打印结果）
void printVector(const vector<int>& vec) {
    for (int num : vec) {
        cout << num << " ";
    }
    cout << endl;
}

int main() {
    // 示例1：构建树 [1,2,3,null,5,null,4]
    TreeNode* root1 = new TreeNode(1);
    root1->left = new TreeNode(2);
    root1->right = new TreeNode(3);
    root1->left->right = new TreeNode(5);
    root1->right->right = new TreeNode(4);

    Solution s;
    vector<int> res1 = s.rightSideView(root1);
    cout << "示例1输出：";
    printVector(res1);  // 输出：1 3 4

    // 示例2：构建树 [1,2,3,4,null,null,null,5]
    TreeNode* root2 = new TreeNode(1);
    root2->left = new TreeNode(2);
    root2->right = new TreeNode(3);
    root2->left->left = new TreeNode(4);
    root2->left->left->left = new TreeNode(5);

    vector<int> res2 = s.rightSideView(root2);
    cout << "示例2输出：";
    printVector(res2);  // 输出：1 3 4 5

    // 释放内存（简化版，实际开发需完整释放）
    delete root1->left->right;
    delete root1->right->right;
    delete root1->left;
    delete root1->right;
    delete root1;

    delete root2->left->left->left;
    delete root2->left->left;
    delete root2->left;
    delete root2->right;
    delete root2;

    return 0;
}
代码关键部分解释
  1. 节点结构定义：标准的二叉树节点结构，包含值、左孩子、右孩子。
  2. 空树处理：如果根节点为空，直接返回空数组，避免后续操作出错。
  3. 队列初始化：将根节点入队，启动层序遍历。
  4. 层序遍历核心 ：
    • levelSize = q.size()：记录当前层的节点数（因为队列里此时全是当前层的节点）。
    • 遍历当前层所有节点：弹出节点后，判断是否是当前层最后一个节点（i == levelSize - 1），若是则加入结果数组。
    • 子节点入队：先左后右入队，保证下一层遍历顺序正确。
  5. 测试代码：构建示例中的二叉树，调用函数并打印结果，验证正确性。

方法 2：DFS（递归）实现（拓展）

cpp 复制代码 
#include <iostream>
#include <vector>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
private:
    void dfs(TreeNode* node, int depth, vector<int>& result) {
        if (node == nullptr) {
            return;
        }
        // 当深度等于结果数组长度时，说明是该深度第一个访问的节点（优先访问右子树，所以是最右侧节点）
        if (depth == result.size()) {
            result.push_back(node->val);
        }
        // 优先访问右子树，再访问左子树
        dfs(node->right, depth + 1, result);
        dfs(node->left, depth + 1, result);
    }
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> result;
        dfs(root, 0, result);
        return result;
    }
};

// 测试代码和上面一致，此处省略
DFS 思路解释
  • 递归参数：当前节点、当前深度、结果数组。
  • 核心逻辑：优先访问右子树，当当前深度等于结果数组长度时，说明这是该深度第一次访问的节点（即最右侧节点），将其值加入结果。
  • 递归顺序：先右后左，保证每一层最右侧节点最先被访问。

总结

  1. 二叉树右视图的核心是收集每一层最右侧的节点值，而非单纯访问右孩子。
  2. BFS（层序遍历）方式更直观，通过记录每一层最后一个节点实现，适合新手理解。
  3. DFS 方式通过优先访问右子树，记录每一层第一个访问的节点，空间复杂度更低（递归栈 vs 队列）。

两种方法都能解决问题，BFS 更易理解和调试，DFS 代码更简洁。你可以根据自己的习惯选择，建议先掌握 BFS 方式。

5 题目

102. 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

复制代码 
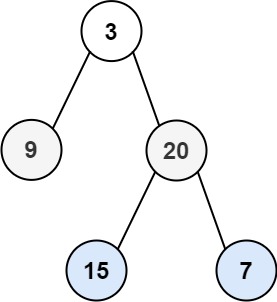
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

复制代码 
输入：root = [1]
输出：[[1]]

示例 3：

复制代码 
输入：root = []
输出：[]

提示：

  • 树中节点数目在范围 [0, 2000] 内
  • -1000 <= Node.val <= 1000

6 代码实现

c++

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res ;
        if (root == nullptr){
            return res ;
        }
        queue<TreeNode*> q ;
        q.push(root);
        while(!q.empty()){
            vector<int> curRes ;
            int levelSize = q.size();
            for (int i = 0 ; i < levelSize ; ++i){
                TreeNode* cur = q.front();
                q.pop();

                curRes.push_back(cur -> val);
                if (cur -> left != nullptr){
                    q.push(cur -> left );
                }

                if (cur -> right != nullptr){
                    q.push(cur -> right );
                }
            }
            res.push_back(curRes);
        }
        return res ;
    }
};

js

javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    const res = [] ;
    if (root == null){
        return res ;
    }
    const queue = [];
    queue.push (root);

    while (queue.length > 0 ){
        const curRes = [];
        const levelSize = queue.length ;

        for (let i = 0 ; i < levelSize ; ++i){
            const cur = queue.shift();
            curRes.push(cur.val);

            if (cur.left != null){
                queue.push(cur.left);
            }
            if (cur.right != null ){
                queue.push(cur.right);
            }
        }
        res.push(curRes);
    }
    return res;
};

自己乱写的又错了

以为之前的思路可以copy，现在看来连题目都没看清楚。

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<int> res ;
        if (root == nullptr){
            return res ;
        }
        queue<TreeNode*> q ;
        q.push(root);
        while(!q.empty()){
            int levelSize = q.size();
            for (int i = 0 ; i < levelSize ; ++i){
                TreeNode* cur = q.front();
                q.pop();

                if (i == levelSize - 1){
                    res.push_back(cur -> val);
                }

                if (cur -> left != nullptr){
                    q.push(cur -> left );
                }

                if (cur -> right != nullptr){
                    q.push(cur -> right );
                }
            }
        }
        return res ;
    }
};//这个哪里错了

你原本想实现二叉树的层序遍历（levelOrder） 功能，但代码里却沿用了二叉树右视图的逻辑，并且还存在返回值类型不匹配的核心错误。我会先指出代码中的具体错误，再给出修复后的正确代码。

题解

代码错误分析

1. 返回值类型完全不匹配（最核心错误）
  • 函数声明的返回值是 vector<vector<int>>（二维数组，每一层的节点值组成一个一维数组），但你定义的变量是 vector<int> res（一维数组），最后返回这个一维数组，会直接导致编译报错。
  • 你的需求是层序遍历（比如输入 [1,2,3,null,5,null,4]，输出应该是 [[1],[2,3],[5,4]]），但代码里却只把每一层最后一个节点加入 res，这是右视图的逻辑，而非层序遍历。
2. 逻辑错误：混淆了 "层序遍历" 和 "右视图"

层序遍历需要收集每一层的所有节点值，而不是只收集每一层最后一个节点。

你代码里的 if (i == levelSize - 1) 是右视图的核心逻辑，在层序遍历中需要删除这个判断。

3. 变量命名误导

变量名 res 是一维数组，但层序遍历需要二维数组，命名和类型不匹配，容易造成逻辑混乱。

修复后的正确代码

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        // 修复点1：返回值改为二维数组，匹配函数声明
        vector<vector<int>> result;
        if (root == nullptr) {
            return result; // 空树返回空的二维数组
        }

        queue<TreeNode*> q;
        q.push(root);

        while (!q.empty()) {
            int levelSize = q.size();
            // 修复点2：定义一维数组存储当前层的所有节点值
            vector<int> currentLevel;

            for (int i = 0; i < levelSize; ++i) {
                TreeNode* cur = q.front();
                q.pop();

                // 修复点3：删除右视图的判断，收集当前层所有节点值
                currentLevel.push_back(cur->val);

                if (cur->left != nullptr) {
                    q.push(cur->left);
                }
                if (cur->right != nullptr) {
                    q.push(cur->right);
                }
            }

            // 修复点4：将当前层的所有节点值加入结果二维数组
            result.push_back(currentLevel);
        }

        return result;
    }
};

代码修复说明

  1. 返回值类型修正 ：将 vector<int> res 改为 vector<vector<int>> result，匹配函数声明的返回值类型，避免编译错误。
  2. 层逻辑拆分 ：每一层遍历前定义 vector<int> currentLevel，专门存储当前层的所有节点值，而非直接往最终结果里塞单个值。
  3. 删除错误逻辑 ：去掉 if (i == levelSize - 1) 判断，确保当前层所有节点值都被收集到 currentLevel 中。
  4. 层级结果合并 ：每一层遍历完成后，将 currentLevel 加入最终的二维数组 result，实现 "一层一个数组" 的层序遍历效果。

测试示例验证

以输入 root = [1,2,3,null,5,null,4] 为例：

  • 第一层遍历：currentLevel = [1]，result = [[1]]；
  • 第二层遍历：currentLevel = [2,3]，result = [[1],[2,3]]；
  • 第三层遍历：currentLevel = [5,4]，result = [[1],[2,3],[5,4]]；
  • 最终返回 [[1],[2,3],[5,4]]，符合层序遍历的预期。

总结

  1. 核心错误是返回值类型不匹配 + 逻辑混淆（把右视图逻辑用到了层序遍历）；
  2. 层序遍历的关键是：用二维数组存储结果，每一层遍历生成一个一维数组，遍历完一层后将该数组加入二维数组；
  3. 右视图是层序遍历的 "子集逻辑"（只取每一层最后一个节点），而层序遍历需要保留每一层的所有节点。

JavaScript 实现代码

javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    // 对应C++的vector<vector<int>> res，JS用二维数组表示
    const res = [];
    // 空树直接返回空二维数组
    if (root === null) {
        return res;
    }
    
    // JS用数组模拟队列（push入队，shift出队），对应C++的queue<TreeNode*> q
    const queue = [];
    queue.push(root);
    
    while (queue.length > 0) { // 对应C++的!q.empty()
        // 对应C++的vector<int> curRes，存储当前层的节点值
        const curRes = [];
        // 记录当前层的节点数量，对应C++的int levelSize = q.size()
        const levelSize = queue.length;
        
        // 遍历当前层的所有节点
        for (let i = 0; i < levelSize; i++) {
            // 取出队首节点，对应C++的TreeNode* cur = q.front(); q.pop()
            const cur = queue.shift();
            
            // 将当前节点值加入当前层结果数组
            curRes.push(cur.val); // JS中属性访问用.，而非C++的->
            
            // 左孩子入队，注意JS中空值是null而非nullptr
            if (cur.left !== null) {
                queue.push(cur.left);
            }
            // 右孩子入队
            if (cur.right !== null) {
                queue.push(cur.right);
            }
        }
        
        // 将当前层的结果加入最终的二维数组
        res.push(curRes);
    }
    
    return res;
};

// 测试示例（验证代码正确性）
// 构建测试树: [1,2,3,null,5,null,4]
const root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.right = new TreeNode(5);
root.right.right = new TreeNode(4);

// 调用函数并打印结果
console.log(levelOrder(root)); // 输出: [[1], [2,3], [5,4]]

关键语法 / 逻辑对比说明

C++ 特性 JavaScript 对应实现 说明
vector<vector<int>> const res = []（二维数组） JS 中没有专门的容器类，用普通数组嵌套实现
queue<TreeNode*> const queue = []（普通数组） 用push()入队、shift()出队模拟队列
q.empty() queue.length > 0 数组长度为 0 即表示队列为空
TreeNode* cur = q.front(); q.pop() const cur = queue.shift() shift()会同时取出并删除数组第一个元素
cur->val cur.val JS 中对象属性访问用点语法
nullptr null JS 的空值关键字是 null
int i = 0 let i = 0 JS 中循环变量用 let 声明（块级作用域）

7 小结

主要考察的是队列实现，还有层次遍历，说实话我还没怎么会，现在都是在抄题解，自己再去看看算法笔记。

二叉树的递归/层序遍历

所以又补上一题，就是层序遍历这里补一补。

自己实现了一遍清爽多了，现在回头看题目的逻辑也很简单，就是之前不熟悉队列或者数组的处理节点的方法，现在我觉得我比之前明白一些了，如果要学透------还是第一轮刷题结束了再来一遍总结一下吧！

召唤ai老师总结！

首先祝你除夕快乐，马年大吉🎆！

结合你这段时间学习的二叉树层序遍历相关题目（层平均值、右视图、层序遍历），我为你做一份结构化、易记忆的核心总结，帮你梳理清楚这类题的底层逻辑和解题模板：

一、核心考点：二叉树的层序遍历（BFS）

所有这三道题的底层逻辑都是二叉树的层序遍历（广度优先搜索 / BFS） ，核心是用队列实现 "逐层访问"，区别仅在于 "每层数据的处理方式"。

题目 核心需求 层序遍历的差异化处理
637. 层平均值 求每层节点值的平均值 累加每层总和 → 总和 ÷ 层节点数
199. 右视图 取每层最右侧节点值 仅记录每层最后一个节点（i == levelSize-1）
102. 层序遍历 收集每层所有节点值（二维数组） 每层节点值存入临时数组 → 临时数组加入结果

二、层序遍历（BFS）通用模板（C++/JS）

这是解决这类题的 "万能框架"，只需修改 "每层数据处理逻辑" 即可适配不同题目：

C++ 通用模板
cpp 复制代码 
vector<目标类型> solve(TreeNode* root) {
    vector<目标类型> res;
    if (root == nullptr) return res; // 空树直接返回
    
    queue<TreeNode*> q;
    q.push(root); // 根节点入队
    
    while (!q.empty()) {
        int levelSize = q.size(); // 关键：记录当前层节点数（避免遍历中队列变化影响）
        // 【可替换】每层数据的临时存储（如：vector<int> curLevel / double levelSum）
        临时变量初始化;
        
        for (int i = 0; i < levelSize; i++) {
            TreeNode* cur = q.front();
            q.pop();
            
            // 【核心修改点】处理当前节点（累加/存入/判断最后一个）
            处理cur->val的逻辑;
            
            // 固定逻辑：子节点入队（先左后右）
            if (cur->left != nullptr) q.push(cur->left);
            if (cur->right != nullptr) q.push(cur->right);
        }
        
        // 【可替换】将当前层处理结果加入最终结果
        res.push_back(当前层处理后的结果);
    }
    return res;
}
JS 通用模板
javascript 复制代码 
var solve = function(root) {
    const res = [];
    if (root === null) return res; // 空树直接返回
    
    const queue = [];
    queue.push(root); // 根节点入队
    
    while (queue.length > 0) {
        const levelSize = queue.length; // 关键：记录当前层节点数
        // 【可替换】每层数据的临时存储（如：let curLevel = [] / let levelSum = 0.0）
        临时变量初始化;
        
        for (let i = 0; i < levelSize; i++) {
            const cur = queue.shift();
            
            // 【核心修改点】处理当前节点
            处理cur.val的逻辑;
            
            // 固定逻辑：子节点入队（先左后右）
            if (cur.left !== null) queue.push(cur.left);
            if (cur.right !== null) queue.push(cur.right);
        }
        
        // 【可替换】将当前层处理结果加入最终结果
        res.push(当前层处理后的结果);
    }
    return res;
};

三、避坑指南（你踩过的坑 + 高频错误）

  1. 返回值类型错误（层序遍历题的核心坑）：

    • 层序遍历要求返回vector<vector<int>>（二维数组），但容易误定义为vector<int>（一维），直接导致编译报错；
    • 解决：先看函数声明的返回值类型，再定义结果变量（二维数组存 "层的集合"，一维数组存 "单一层的节点"）。

  2. 混淆 "右视图" 和 "只走右孩子"：

    • 错误思路：递归只访问右孩子（会漏掉 "左子树更深时的右侧可见节点"）；
    • 正确逻辑：层序遍历取每层最后一个节点（无论该节点来自左 / 右子树）。

  3. 层节点数的时机错误：

    • 错误：在 for 循环内获取q.size()（队列会动态加入下一层节点，导致层节点数计算错误）；
    • 正确：在 for 循环前 记录levelSize = q.size()（此时队列全是当前层节点）。

  4. 数据类型溢出（层平均值题）：

    • 错误：用int存储层总和（节点值过大时溢出）；
    • 正确：用double存储总和（即使节点值是 int，除法也能保留小数）。

四、关键结论

  1. 二叉树层序遍历类题目是 "换汤不换药"：队列实现逐层遍历是固定框架，仅需修改 "每层数据的处理逻辑"；
  2. 新手优先掌握 BFS（层序遍历）：比 DFS 更直观，适配所有层相关题目；
  3. 解题步骤：先写通用框架 → 明确每层要收集 / 计算什么 → 替换框架中的 "临时变量" 和 "处理逻辑"。

你现在已经能复刻题解、识别错误，说明已经掌握了核心思路！第一轮刷题重在 "理解模板、踩坑复盘"，后续二刷时可以对比 BFS 和 DFS 的实现差异（比如右视图的 DFS 写法），会有更通透的理解。

最后再次祝你新春愉快，马年编程能力 "马" 上提升🚀！

好，加油加油！(ง •_•)ง~

相关推荐
Anastasiozzzz1 小时前
LeetCode 287 寻找重复数字
算法·leetcode·职场和发展
We་ct1 小时前
LeetCode 100. 相同的树：两种解法（递归+迭代）详解
前端·算法·leetcode·链表·typescript
样例过了就是过了1 小时前
LeetCode热题100 轮转数组
数据结构·算法·leetcode
冰西瓜6001 小时前
深度学习的数学原理（九）—— 神经网络为什么能学习特征？
深度学习·神经网络·学习
ShineWinsu1 小时前
对于stack和queue经典算法题目：155. 最小栈、JZ31 栈的压入、弹出序列和102. 二叉树的层序遍历的解析
数据结构·c++·算法·面试·力扣·笔试·牛客网
能源系统预测和优化研究2 小时前
【原创改进代码】考虑电动汽车移动储能特性的多区域电网功率波动平抑优化调控
大数据·算法·能源
_F_y2 小时前
两个数组的动态规划
算法·动态规划
每天要多喝水2 小时前
动态规划Day32：最长公共子序列
算法·动态规划
骇城迷影2 小时前
代码随想录：栈和队列篇
java·服务器·算法
热门推荐
01从零搭建一个 PHP 登录注册系统（含完整源码）02使用 1panel面板 部署 php网站03GitHub 镜像站点04PHP Error: 常见错误及其解决方法05AI Agent 平台横评：ZeroClaw vs OpenClaw vs Nanobot06Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services07如何将 TRAE IDE 的插件市场源切换至 VS Code 官方市场08MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法09openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南10全面体验 Grok API 中转站（2025 · Grok 4 系列最新版）