刷题时被矩阵的旋转操作卡了n次了，决定写篇博客总结一下
思路参考：第40次CSP认证前四题 - Oaths - 博客园
https://www.cnblogs.com/oaths/articles/19327767
这位大佬的实现个人感觉是比较符合直觉的（也比较好记）
翻转
矩阵坐标从（1，1）开始
翻转第x0到第x1行，第y0到第y1列的子矩阵，oi=1即上下翻转，oi=-1就左右翻转
cpp
void fan_zhuan(int x0, int y0, int x1, int y1, int oi){
if(oi == 1){ //上下翻转
while(x0 < x1){
for(int i = y0; i <= y1; i ++ ){
swap(a[x0][i], a[x1][i]);
}
x0 ++ ; x1 -- ;
}
}
else{//左右翻转
while(y0 < y1){
for(int i = x0; i <= x1; i ++ ){
swap(a[i][y0], a[i][y1]);
}
y0 ++ ; y1 -- ;
}
}
}旋转
注意：逆时针转i次90度==顺时针转4-i次90度；此处代码实现顺时针旋转
a为原矩阵，b为辅助矩阵，如果是旋转整个边长为l的正方形矩阵，公式为：
- 顺时针转90度：b[j][l-i+1] = a[i][j];
- 顺时针转180度：b[l-i+1][l-j+1] = a[i][j];
- 顺时针转270度：b[l-j+1][i] = a[i][j];
只旋转左上角为（x，y），边长为l的l*l小矩阵，只需在a的下标加上偏移量，小矩阵第i行，即原矩阵的x+i-1行，小矩阵的第j列，即原矩阵的y+j-1行
- 顺时针转90度：b[j][l-i+1] = a[x+i-1][y+j-1];
- 顺时针转180度：b[l-i+1][l-j+1] = a[x+i-1][y+j-1];
- 顺时针转270度：b[l-j+1][i] = a[x+i-1][y+j-1];
cpp
/*
左上角坐标(x,y), 边长l，顺时针旋转90度*t次
*/
void xuan_zhuan(int x,int y,int l,int t) { //time 次数
char b[N][N]; //辅助矩阵，坐标从(1,1)开始 只存需要旋转的小矩阵
if(t==0) return; //旋转0次
if(t==1) //顺时针转90度 90*1
for (int i = 1; i <= l; i++) {
for (int j = 1; j <= l; j++) {
b[j][l-i+1] = a[x+i-1][y+j-1];
}
}
else if(t==2){ //顺时针转180度 90*2次
for (int i = 1; i <= l; i++)
for (int j = 1; j <= l; j++) {
b[l-i+1][l-j+1] = a[x+i-1][y+j-1];
}
}
else if(t==3){//顺时针转270度 90*3次
for (int i = 1; i <= l; i++)
for (int j = 1; j <= l; j++) {
b[l-j+1][i] = a[x+i-1][y+j-1];
}
}
//复制回去
// for(int i = 1; i <= l ; i ++ )
// for(int j = 1 ; j <= l; j ++ ){
// a[x + i - 1][y + j - 1] = b[i][j];
// }
// 常数优化：使用 memcpy 进行整行拷贝
for (int i = 1; i <= l; i++) {
memcpy(&a[x + i - 1][y], &b[i][1], l*sizeof(char)); //memcpy(目标地址, 源地址, 字节数)
}
} 测试代码：
cpp
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
const int N=405;
char a[N][N]; //1~N行 1~ 列
int z; //正方形边长
void print()
{
for(int i=1;i<=z;i++){
for(int j=1;j<=z;j++)
cout<<a[i][j];
cout<<endl;
}
}
/*
翻转第x0到第x1行，第y0到第y1列的矩阵，oi=1即上下翻转，oi=-1就左右翻转
*/
void fan_zhuan(int x0, int y0, int x1, int y1, int oi){
if(oi == 1){ //上下翻转
while(x0 < x1){
for(int i = y0; i <= y1; i ++ ){
swap(a[x0][i], a[x1][i]);
}
x0 ++ ; x1 -- ;
}
}
else{//左右翻转
while(y0 < y1){
for(int i = x0; i <= x1; i ++ ){
swap(a[i][y0], a[i][y1]);
}
y0 ++ ; y1 -- ;
}
}
cout<<"======="<<endl;
print();
cout<<"======="<<endl;
}
/*
左上角坐标(x,y), 边长l，顺时针旋转90度*t次
*/
void xuan_zhuan(int x,int y,int l,int t) { //time 顺时针转90度的次数
char b[l+5][l+5]; //辅助矩阵，坐标从(1,1)开始,只存需要旋转的小矩阵
if(t==0) return; //旋转0次
if(t==1) //顺时针转90度 90*1
for (int i = 1; i <= l; i++) {
for (int j = 1; j <= l; j++) {
b[j][l-i+1] = a[x+i-1][y+j-1];
}
}
else if(t==2){ //顺时针转180度 90*2次
for (int i = 1; i <= l; i++)
for (int j = 1; j <= l; j++) {
b[l-i+1][l-j+1] = a[x+i-1][y+j-1];
}
}
else if(t==3){//顺时针转270度 90*3次
for (int i = 1; i <= l; i++)
for (int j = 1; j <= l; j++) {
b[l-j+1][i] = a[x+i-1][y+j-1];
}
}
//复制回去
// for(int i = 1; i <= l ; i ++ )
// for(int j = 1 ; j <= l; j ++ ){
// a[x + i - 1][y + j - 1] = b[i][j];
// }
// 常数优化：使用 memcpy 进行整行拷贝
for (int i = 1; i <= l; i++) {
memcpy(&a[x + i - 1][y], &b[i][1], l*sizeof(char)); //memcpy(目标地址, 源地址, 字节数)
}
cout<<"======="<<endl;
print();
cout<<"======="<<endl;
}
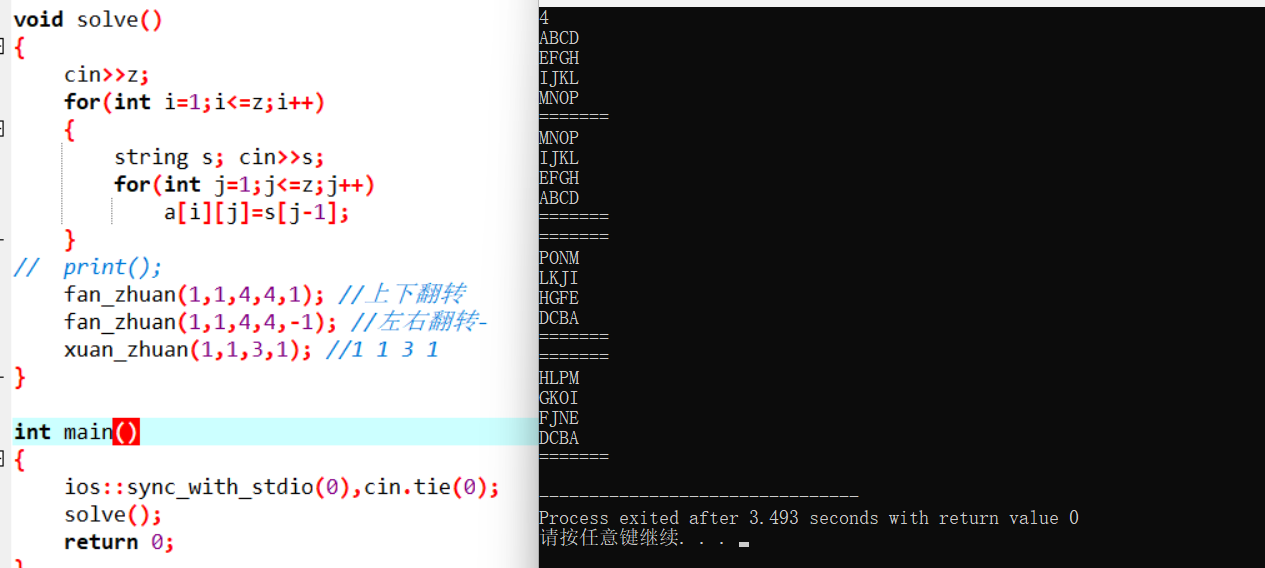
void solve()
{
cin>>z;
for(int i=1;i<=z;i++)
{
string s; cin>>s;
for(int j=1;j<=z;j++)
a[i][j]=s[j-1];
}
// print();
fan_zhuan(1,1,4,4,1); //上下翻转
fan_zhuan(1,1,4,4,-1); //左右翻转-
xuan_zhuan(1,1,3,1); //1 1 3 1
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0);
solve();
return 0;
}
/*
4
ABCD
EFGH
IJKL
MNOP
*/ 