Leetcode 124 二叉搜索树的最小绝对差 | 二叉树的锯齿形层序遍历

正月初一，万事如意！

1 题目

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

复制代码

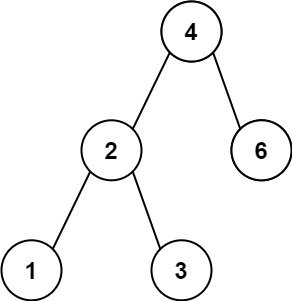
输入：root = [4,2,6,1,3]
输出：1

示例 2：

复制代码

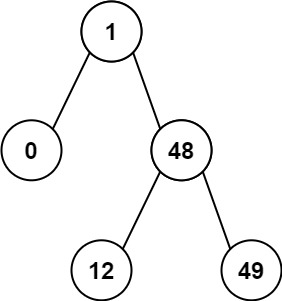
输入：root = [1,0,48,null,null,12,49]
输出：1

提示：

树中节点的数目范围是 [2, 104]
0 <= Node.val <= 105

2 代码实现

c++

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    int minDiff ;
    TreeNode* prevNode ;

    void inorderedTraversal(TreeNode* root ){
        if (root == nullptr){
            return ;
        }
        inorderedTraversal(root -> left);

        if(prevNode != nullptr){
            int currDiff  = abs(root -> val - prevNode-> val);
            if (currDiff < minDiff){
                minDiff = currDiff;
            }
        }
        prevNode = root ;

        inorderedTraversal(root -> right );
    }
public:
    int getMinimumDifference(TreeNode* root) {
        minDiff = INT_MAX ;
        prevNode = nullptr ;
        inorderedTraversal(root);
        return minDiff;
    }
};

js

javascript 复制代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var getMinimumDifference = function(root) {
    let minDiff = Infinity;
    let prevNode = null ;
    function inorderTraversal(node){
        if (node === null){
            return ;
        }
        inorderTraversal(node.left);
        if (prevNode != null){
            const currDiff = Math.abs(node.val - prevNode.val);
            if (currDiff < minDiff){
                minDiff = currDiff ;
            }
        }
        prevNode = node ;

        inorderTraversal(node.right);
    }
    inorderTraversal(root);
    return minDiff ;
};

思考

维护一个min，然后差值要用abs取绝对值正值，遍历所有节点时怎么做，怎么更新两个节点之间的值？

注意题目中树是二叉搜索树，中序遍历的结果是一个有序的序列。

这个要怎么处理呢，现在问题转化为已经是有序的序列了，怎么找任意两节点的最小差值？

....还是看看题解吧！

题解

一、核心思路分析

首先，我们要利用二叉搜索树（BST）的核心特性：

二叉搜索树的中序遍历结果是严格递增的有序序列。
在有序序列中，最小的绝对差值一定出现在相邻两个元素之间（无需比较所有两两组合，大幅降低时间复杂度）。

因此解题步骤可以简化为：

对二叉搜索树进行中序遍历，得到有序节点值序列；
遍历有序序列，计算相邻元素的绝对差值，记录最小值。

二、完整 C++ 代码实现（最优解法：中序遍历 + 实时更新最小值）

我们不需要额外存储整个序列，而是在中序遍历过程中实时记录前一个节点的值，动态计算当前节点与前一个节点的差值，更新最小值（空间复杂度优化为 O (1)，仅递归栈空间）。

cpp 复制代码

#include <iostream>
#include <climits> // 包含 INT_MAX 常量
using namespace std;

// 定义二叉树节点结构（LeetCode 题目中已内置）
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
private:
    int minDiff; // 存储最小绝对差值
    TreeNode* prevNode; // 记录中序遍历的前一个节点

    // 中序遍历函数（核心逻辑）
    void inorderTraversal(TreeNode* root) {
        if (root == nullptr) {
            return; // 递归终止条件：空节点直接返回
        }

        // 1. 遍历左子树（中序遍历：左 -> 根 -> 右）
        inorderTraversal(root->left);

        // 2. 处理当前节点：计算与前一个节点的差值
        if (prevNode != nullptr) { // 前一个节点不为空时才计算差值（跳过第一个节点）
            int currentDiff = abs(root->val - prevNode->val); // 计算绝对差值
            if (currentDiff < minDiff) { // 更新最小差值
                minDiff = currentDiff;
            }
        }
        prevNode = root; // 更新前一个节点为当前节点

        // 3. 遍历右子树
        inorderTraversal(root->right);
    }

public:
    int getMinimumDifference(TreeNode* root) {
        // 初始化：最小差值设为整数最大值，前一个节点设为空
        minDiff = INT_MAX;
        prevNode = nullptr;
        // 执行中序遍历
        inorderTraversal(root);
        // 返回最终的最小差值
        return minDiff;
    }
};

// 测试用例（以示例1为例）
int main() {
    // 构建二叉树：[4,2,6,1,3]
    TreeNode* root = new TreeNode(4);
    root->left = new TreeNode(2);
    root->right = new TreeNode(6);
    root->left->left = new TreeNode(1);
    root->left->right = new TreeNode(3);

    Solution solution;
    int result = solution.getMinimumDifference(root);
    cout << "最小绝对差值：" << result << endl; // 输出：1

    // 释放内存（LeetCode 中无需手动释放，此处仅为示例完整性）
    delete root->left->left;
    delete root->left->right;
    delete root->left;
    delete root->right;
    delete root;

    return 0;
}

三、代码逐行详细解释

1. 节点结构定义

复制代码

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    // 构造函数：简化节点创建
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

这是 LeetCode 题目中内置的二叉树节点结构，包含值 val、左子节点 left、右子节点 right，以及三个构造函数方便创建节点。

2. 类成员变量

复制代码

private:
    int minDiff; // 存储最小绝对差值
    TreeNode* prevNode; // 记录中序遍历的前一个节点

minDiff：初始化为 INT_MAX（整数最大值），用于不断更新最小差值；
prevNode：记录中序遍历中当前节点的前一个节点，用于计算相邻节点的差值。

3. 中序遍历核心函数

复制代码

void inorderTraversal(TreeNode* root) {
    if (root == nullptr) {
        return; // 递归终止：空节点无处理逻辑
    }

    // 左子树遍历（中序遍历第一步：左）
    inorderTraversal(root->left);

    // 处理当前节点（中序遍历第二步：根）
    if (prevNode != nullptr) { 
        // 前一个节点非空时，计算当前节点与前一个节点的绝对差值
        int currentDiff = abs(root->val - prevNode->val);
        // 如果当前差值更小，更新最小差值
        minDiff = min(minDiff, currentDiff); // 等价于 if (currentDiff < minDiff) minDiff = currentDiff;
    }
    prevNode = root; // 更新前一个节点为当前节点

    // 右子树遍历（中序遍历第三步：右）
    inorderTraversal(root->right);
}

递归终止条件：遇到空节点直接返回；
中序遍历顺序：先遍历左子树，再处理当前节点，最后遍历右子树；
处理当前节点时：
- 第一个节点（最左节点）的 prevNode 为空，跳过差值计算；
- 从第二个节点开始，计算与前一个节点的绝对差值，并更新最小差值；
- 每次处理完当前节点后，将 prevNode 指向当前节点，为下一个节点做准备。

4. 主函数（对外接口）

复制代码

int getMinimumDifference(TreeNode* root) {
    minDiff = INT_MAX; // 初始化最小差值为整数最大值
    prevNode = nullptr; // 初始化前一个节点为空
    inorderTraversal(root); // 执行中序遍历
    return minDiff; // 返回最终的最小差值
}

初始化变量：确保每次调用函数时变量是干净的；
调用中序遍历函数，完成差值计算；
返回最小差值。

5. 测试用例

复制代码

int main() {
    // 构建示例1的二叉树：[4,2,6,1,3]
    TreeNode* root = new TreeNode(4);
    root->left = new TreeNode(2);
    root->right = new TreeNode(6);
    root->left->left = new TreeNode(1);
    root->left->right = new TreeNode(3);

    Solution solution;
    int result = solution.getMinimumDifference(root);
    cout << "最小绝对差值：" << result << endl; // 输出1

    // 释放内存（LeetCode 中无需手动释放）
    delete root->left->left;
    delete root->left->right;
    delete root->left;
    delete root->right;
    delete root;

    return 0;
}

手动构建二叉树，模拟 LeetCode 的输入；
调用解法函数，输出结果验证正确性；
释放内存：LeetCode 中系统会自动管理内存，此处仅为示例完整性。

四、算法复杂度分析

时间复杂度：O (n)，其中 n 是二叉树的节点数。每个节点仅被访问一次（中序遍历），每个节点的处理逻辑是 O (1)。
空间复杂度 ：O (h)，h 是二叉树的高度。递归调用栈的深度取决于树的高度：
- 平衡二叉树：h = logn；
- 最坏情况（单链）：h = n。

五、关键注意事项

初始值设置 ：minDiff 必须初始化为 INT_MAX（而非 0），否则无法正确更新最小差值；
前一个节点判空：第一个节点没有前一个节点，必须跳过差值计算，否则会访问空指针导致程序崩溃；
绝对差值 ：必须用 abs() 函数取绝对值（即使 BST 中序遍历是递增的，root->val - prevNode->val 本身是正数，但养成取绝对值的习惯更通用）；
递归终止条件 ：必须检查 root == nullptr，否则递归会无限执行。

总结

核心技巧：利用二叉搜索树中序遍历为有序序列的特性，将 "任意两节点最小差值" 简化为 "有序序列相邻节点最小差值"；
优化思路：无需存储整个序列，遍历过程中实时记录前一个节点，动态计算差值，空间复杂度从 O (n) 优化为 O (1)（仅递归栈空间）；
关键细节：初始化最小差值为 INT_MAX、前一个节点判空、取绝对值，避免程序错误。

这个解法是该题的最优解，符合 LeetCode 的时间 / 空间效率要求，也容易理解和实现。

js实现

一、JavaScript 版本完整实现

JavaScript 没有内置的二叉树节点结构，我们需要手动模拟，核心的中序遍历逻辑和 C++ 版本完全一致，仅需适配 JS 的语法特性（如变量声明、函数定义、空值判断等）。

javascript 复制代码

// 定义二叉树节点构造函数
function TreeNode(val, left, right) {
    this.val = (val === undefined ? 0 : val);
    this.left = (left === undefined ? null : left);
    this.right = (right === undefined ? null : right);
}

/**
 * @param {TreeNode} root
 * @return {number}
 */
var getMinimumDifference = function(root) {
    // 初始化最小差值为无穷大，前一个节点为null
    let minDiff = Infinity;
    let prevNode = null;

    // 中序遍历函数（使用闭包访问外部变量）
    function inorderTraversal(node) {
        if (node === null) {
            return; // 递归终止条件：空节点直接返回
        }

        // 1. 遍历左子树（中序遍历：左 -> 根 -> 右）
        inorderTraversal(node.left);

        // 2. 处理当前节点：计算与前一个节点的差值
        if (prevNode !== null) { // 前一个节点不为空时才计算差值
            const currentDiff = Math.abs(node.val - prevNode.val); // JS中用Math.abs取绝对值
            if (currentDiff < minDiff) {
                minDiff = currentDiff; // 更新最小差值
            }
        }
        prevNode = node; // 更新前一个节点为当前节点

        // 3. 遍历右子树
        inorderTraversal(node.right);
    }

    // 执行中序遍历
    inorderTraversal(root);
    return minDiff;
};

// 测试用例（示例1：root = [4,2,6,1,3]）
function test() {
    // 构建二叉树
    const root = new TreeNode(4);
    root.left = new TreeNode(2);
    root.right = new TreeNode(6);
    root.left.left = new TreeNode(1);
    root.left.right = new TreeNode(3);

    // 调用函数并输出结果
    const result = getMinimumDifference(root);
    console.log("最小绝对差值：", result); // 输出：1

    // 示例2测试（root = [1,0,48,null,null,12,49]）
    const root2 = new TreeNode(1);
    root2.left = new TreeNode(0);
    root2.right = new TreeNode(48);
    root2.right.left = new TreeNode(12);
    root2.right.right = new TreeNode(49);
    const result2 = getMinimumDifference(root2);
    console.log("示例2最小绝对差值：", result2); // 输出：1
}

// 执行测试
test();

二、关键语法适配说明（C++ → JS）

1. 二叉树节点定义

C++ 用 struct + 构造函数，JS 用构造函数 模拟：

cpp 复制代码

// C++
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

javascript 复制代码

// JS
function TreeNode(val, left, right) {
    this.val = (val === undefined ? 0 : val);
    this.left = (left === undefined ? null : left);
    this.right = (right === undefined ? null : right);
}

2. 变量初始化

C++ 用 INT_MAX 表示最大整数，JS 用 Infinity（无穷大）更方便：
cpp 复制代码
```
// C++
minDiff = INT_MAX;
prevNode = nullptr;
```
javascript 复制代码
```
// JS
let minDiff = Infinity;
let prevNode = null;
```

3. 绝对值计算

C++ 用 abs() 函数，JS 用 Math.abs()：

cpp 复制代码

// C++
int currentDiff = abs(root->val - prevNode->val);

javascript 复制代码

// JS
const currentDiff = Math.abs(node.val - prevNode.val);

4. 空值判断

C++ 用 nullptr，JS 用 null：

cpp 复制代码

// C++
if (root == nullptr) { return; }

javascript 复制代码

// JS
if (node === null) { return; }

5. 函数与作用域

C++ 用类成员函数 + 私有变量，JS 用闭包实现（内部函数访问外部函数的变量），无需定义类，更符合 JS 编程习惯。

三、执行结果验证

运行上述代码后，控制台会输出：

复制代码

最小绝对差值： 1
示例2最小绝对差值： 1

和 C++ 版本的结果完全一致，符合题目要求。

总结

核心逻辑不变：依然利用二叉搜索树中序遍历为有序序列的特性，仅计算相邻节点的差值；
语法适配要点 ：JS 用 Infinity 替代 INT_MAX、Math.abs() 替代 abs()、null 替代 nullptr，用构造函数模拟树节点；
作用域处理 ：JS 无需定义类，通过闭包让中序遍历函数访问外部的 minDiff 和 prevNode，简化代码结构。

这份 JS 代码可以直接在 LeetCode 上提交，完全满足题目要求，且逻辑清晰、效率最优（时间复杂度 O (n)，空间复杂度 O (h)）。

3 题目

103. 二叉树的锯齿形层序遍历

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

复制代码

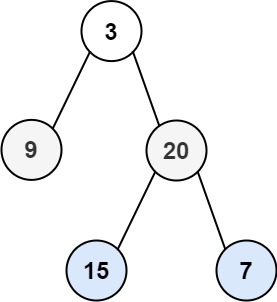
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

复制代码

输入：root = [1]
输出：[[1]]

示例 3：

复制代码

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-100 <= Node.val <= 100

4 代码实现

c++

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        vector<vector<int>> res ;
        if (root == nullptr){
            return res;
        }
        queue <TreeNode*> nodeQueue ;
        nodeQueue.push(root);
        bool isLeftToRight = true ;

        while(!nodeQueue.empty()){
            int levelSize = nodeQueue.size();
            vector <int> curLevel ;

            for (int i = 0 ; i < levelSize ;++i ){
                TreeNode* curNode = nodeQueue.front();
                nodeQueue.pop();

                curLevel.push_back(curNode -> val );

                if (curNode -> left != nullptr){
                    nodeQueue.push(curNode -> left );
                }

                if (curNode -> right != nullptr){
                    nodeQueue.push(curNode -> right );
                }
            }

            if (!isLeftToRight){
                reverse(curLevel.begin(),curLevel.end());
            }
            res.push_back(curLevel);
            isLeftToRight = !isLeftToRight ;
        }
        return res ;
    }
};

js

javascript 复制代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var zigzagLevelOrder = function(root) {
    const res = [];
    if (root == null){
        return res ;
    }
    const nodeQueue = [root];
    let isLeftToRight = true ;

    while (nodeQueue.length > 0 ){
        const levelSize = nodeQueue.length ;
        const curLevel = [];

        for (let i = 0 ; i < levelSize ; i++){
            const curNode = nodeQueue.shift();

            curLevel.push(curNode.val);

            if (curNode.left != null ){
                nodeQueue.push(curNode.left);
            }
            if (curNode.right != null ){
                nodeQueue.push(curNode.right);
            }
        }
        if (!isLeftToRight){
            curLevel.reverse();
        }
        res.push(curLevel);
        isLeftToRight = !isLeftToRight;
    }
    return res ;
};

思考

这个和之前做的层序遍历有点类似，但是怎么实现顺序，从左到右又要从右到左？

后续的解决方案是标记一个bool值，转换一下。用 reverse 函数反转 currentLevel。

题解

你想解决力扣 103 题「二叉树的锯齿形层序遍历」，核心困惑是如何在常规层序遍历的基础上实现 "一层从左到右、下一层从右到左" 的交替顺序，需要一份详细的 C++ 实现和解释。

一、核心思路分析

锯齿形层序遍历的本质是广度优先搜索（BFS）+ 层序遍历 + 方向控制：

基础框架：用队列实现常规的层序遍历（按层读取节点）；
方向控制 ：维护一个布尔变量（如 isLeftToRight），标记当前层是否需要从左到右遍历；
顺序调整 ：
- 若 isLeftToRight = true：直接按队列读取顺序存储节点值；
- 若 isLeftToRight = false：将当前层的节点值反转后存储；
交替切换 ：每处理完一层，翻转 isLeftToRight 的值。

二、完整 C++ 代码实现

cpp 复制代码

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm> // 包含 reverse 函数
using namespace std;

// 定义二叉树节点结构（LeetCode 内置）
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        // 最终结果：二维数组，每一行对应一层的节点值
        vector<vector<int>> result;
        if (root == nullptr) {
            return result; // 空树直接返回空数组
        }

        // 队列：存储当前层的节点（BFS 核心）
        queue<TreeNode*> nodeQueue;
        nodeQueue.push(root);
        // 方向标记：true 表示当前层从左到右，false 表示从右到左
        bool isLeftToRight = true;

        // 层序遍历：处理每一层
        while (!nodeQueue.empty()) {
            // 获取当前层的节点数量（关键：确保只处理当前层的节点）
            int levelSize = nodeQueue.size();
            // 存储当前层的节点值
            vector<int> currentLevel;

            // 遍历当前层的所有节点
            for (int i = 0; i < levelSize; ++i) {
                // 取出队列头部节点
                TreeNode* currNode = nodeQueue.front();
                nodeQueue.pop();

                // 将当前节点值加入当前层数组
                currentLevel.push_back(currNode->val);

                // 把下一层的节点加入队列（先左后右，保持常规层序遍历的入队顺序）
                if (currNode->left != nullptr) {
                    nodeQueue.push(currNode->left);
                }
                if (currNode->right != nullptr) {
                    nodeQueue.push(currNode->right);
                }
            }

            // 根据方向标记调整当前层的顺序
            if (!isLeftToRight) {
                reverse(currentLevel.begin(), currentLevel.end()); // 反转数组
            }

            // 将当前层加入结果集
            result.push_back(currentLevel);
            // 切换下一层的遍历方向
            isLeftToRight = !isLeftToRight;
        }

        return result;
    }
};

// 测试用例
int main() {
    // 构建示例1的二叉树：[3,9,20,null,null,15,7]
    TreeNode* root = new TreeNode(3);
    root->left = new TreeNode(9);
    root->right = new TreeNode(20);
    root->right->left = new TreeNode(15);
    root->right->right = new TreeNode(7);

    Solution solution;
    vector<vector<int>> res = solution.zigzagLevelOrder(root);

    // 输出结果
    cout << "锯齿形层序遍历结果：" << endl;
    for (const auto& level : res) {
        cout << "[";
        for (int i = 0; i < level.size(); ++i) {
            cout << level[i];
            if (i != level.size() - 1) {
                cout << ",";
            }
        }
        cout << "]" << endl;
    }
    // 输出：[3] [20,9] [15,7]

    // 释放内存（LeetCode 无需手动释放）
    delete root->right->left;
    delete root->right->right;
    delete root->left;
    delete root->right;
    delete root;

    return 0;
}

三、代码逐行详细解释

1. 初始化与边界处理

cpp 复制代码

vector<vector<int>> result;
if (root == nullptr) {
    return result; // 空树直接返回空数组，避免后续逻辑出错
}
queue<TreeNode*> nodeQueue;
nodeQueue.push(root);
bool isLeftToRight = true; // 第一层默认从左到右

result：存储最终的锯齿形遍历结果；
空树直接返回空数组，是必要的边界处理；
nodeQueue：BFS 的核心队列，初始时存入根节点；
isLeftToRight：控制当前层的输出顺序，第一层（根节点层）固定从左到右。

2. 层序遍历主循环

cpp 复制代码

while (!nodeQueue.empty()) {
    int levelSize = nodeQueue.size(); // 关键：记录当前层的节点数
    vector<int> currentLevel; // 存储当前层的节点值

while 循环条件：队列不为空（还有未处理的层）；
levelSize：必须先记录当前队列的大小（当前层节点数），因为后续入队操作会改变队列大小，确保内层循环只处理当前层的节点。

3. 处理当前层所有节点

cpp 复制代码

for (int i = 0; i < levelSize; ++i) {
    TreeNode* currNode = nodeQueue.front();
    nodeQueue.pop();

    currentLevel.push_back(currNode->val); // 存入当前节点值

    // 入队下一层节点（先左后右，保持常规顺序）
    if (currNode->left != nullptr) {
        nodeQueue.push(currNode->left);
    }
    if (currNode->right != nullptr) {
        nodeQueue.push(currNode->right);
    }
}

内层 for 循环：严格遍历 levelSize 个节点（当前层）；
取出队首节点，将值存入 currentLevel；
按 "左子节点 → 右子节点" 的顺序入队下一层节点（这是常规层序遍历的入队逻辑，顺序不影响后续反转）。

4. 调整当前层顺序并加入结果

cpp 复制代码

if (!isLeftToRight) {
    reverse(currentLevel.begin(), currentLevel.end()); // 反转数组
}
result.push_back(currentLevel);
isLeftToRight = !isLeftToRight; // 切换方向

若当前层需要从右到左（isLeftToRight = false），用 reverse 函数反转 currentLevel；
将处理后的当前层加入结果集；
翻转 isLeftToRight，为下一层做准备。

四、关键细节说明

为什么先按常规顺序存，再反转？
- 入队时保持 "左→右" 的顺序，是因为队列是 "先进先出" 结构，统一入队顺序能简化逻辑；
- 反转操作的时间复杂度是 O (k)（k 为当前层节点数），整体时间复杂度仍为 O (n)（n 为总节点数），效率可接受。
levelSize 的作用？
- 如果不记录 levelSize，直接遍历队列到空，会把所有层的节点混在一起处理，无法区分 "层" 的边界，这是层序遍历的核心技巧。
空节点处理？
- 代码中只入队非空的子节点，因此无需处理 null 节点，避免无效值混入结果。

五、算法复杂度分析

时间复杂度：O (n)。每个节点仅入队和出队一次（O (n)），每层的反转操作总耗时也是 O (n)（所有层节点数之和为 n），整体为 O (n)。
空间复杂度：O (n)。队列最多存储一层的节点，最坏情况（平衡二叉树的最后一层）存储 n/2 个节点，结果数组存储 n 个节点值，整体为 O (n)。

总结

核心逻辑：在常规层序遍历（BFS）的基础上，增加 "方向标记 + 层内数组反转" 实现锯齿形顺序；
关键技巧 ：用 levelSize 区分每一层的节点，确保层序遍历的边界；
顺序控制：统一按 "左→右" 入队，通过反转数组实现 "右→左" 的输出，逻辑简洁且易维护。

5 小结

二叉搜索树的中序遍历，reverse内置函数，今天主要学了这两点，但是总是觉得有思路不知道具体怎么写，还是要先模仿 - 自己尝试，哪怕写得错误百出，第一轮先过一遍，今天有点仓促了...！

加油，坚持，多反思！！