【胶囊网络 - 简明教程】 02-1 整体架构设计
目录
- [1. 架构总览](#1. 架构总览)
- [2. 编码器设计](#2. 编码器设计)
- [3. 解码器设计](#3. 解码器设计)
- [4. 数据流分析](#4. 数据流分析)
- [5. 设计哲学](#5. 设计哲学)
1. 架构总览
1.1 完整 Capsule Network 结构
基于本项目(Capsule_Network.ipynb)实现的架构,完整的胶囊网络由以下核心组件构成:
架构可视化
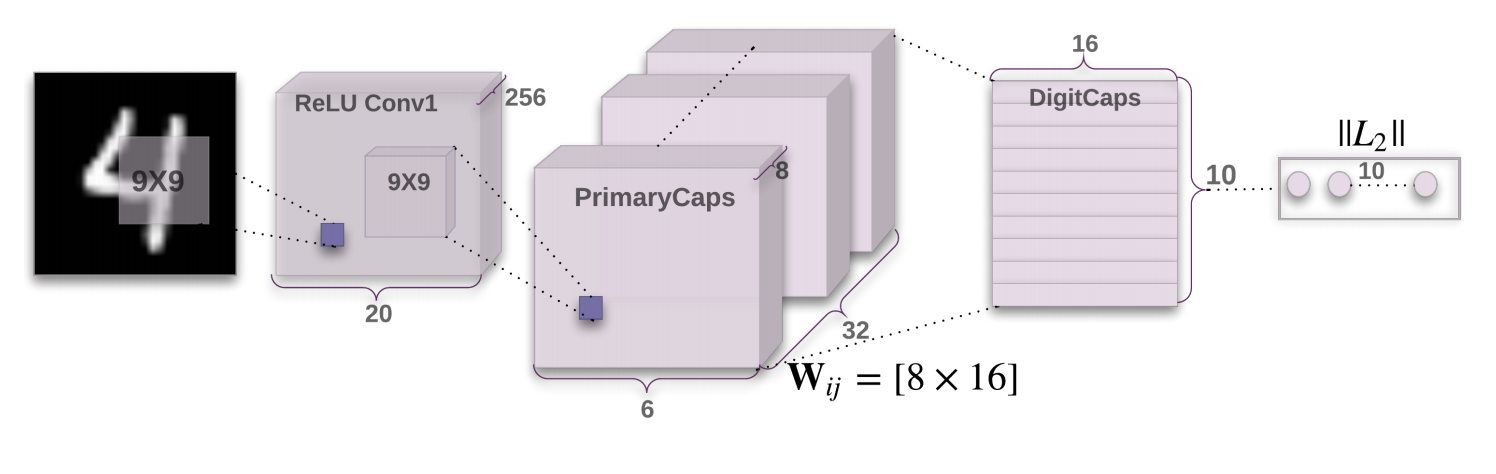
图 1:完整的 Capsule Network 架构(来源:原论文)
这张图展示了 CapsNet 的完整数据流:
- 左侧:编码器部分,从输入图像到 DigitCaps 的层次化特征提取
- 右侧:解码器部分,从胶囊表示重建原始图像
- 中间:动态路由机制,连接 PrimaryCaps 和 DigitCaps
解码器 Decoder
编码器 Encoder
输入层
输入图像
28×28×1 灰度
Conv1 卷积层
256@9×9 stride=1
输出:20×20×256
PrimaryCaps
8 个胶囊
输出:1152×8
DigitCaps
10 个数字胶囊
输出:16×10
FC1: 160→512
FC2: 512→1024
FC3: 1024→784
重建图像
1.2 核心组件功能
| 组件 | 功能 | 输入维度 | 输出维度 |
|---|---|---|---|
| Conv1 | 提取基础特征 | 28×28×1 | 20×20×256 |
| PrimaryCaps | 形成初级胶囊 | 20×20×256 | 1152×8 |
| DigitCaps | 高级语义表示 | 1152×8 | 16×10 |
| Decoder | 重建验证 | 160 | 784 |
2. 编码器设计
2.1 第一层:卷积层(ConvLayer)
设计目标
卷积层负责从原始像素中提取低级特征,如边缘、角点、纹理等。
关键参数
python
class ConvLayer(nn.Module):
def __init__(self, in_channels=1, out_channels=256):
self.conv = nn.Conv2d(
in_channels=1, # 输入:灰度图像
out_channels=256, # 输出:256 个特征图
kernel_size=9, # 9×9 卷积核
stride=1, # 步长为 1
padding=0 # 无填充
)维度计算详解
输入尺寸:28×28×1
卷积操作:
- 卷积核大小:9×9
- 步长:1
- 填充:0
输出尺寸计算公式:
output_size = (input_size - kernel_size + 2*padding) / stride + 1
= (28 - 9 + 0) / 1 + 1
= 20
输出维度:20×20×256可视化理解
输出特征图
卷积操作
输入
输入图像
28×28×1
9×9 卷积核
滑动扫描
特征图 1
垂直边缘
特征图 2
水平边缘
特征图 3
45°斜边
...
特征图 256
复杂纹理
激活函数选择
python
features = F.relu(self.conv(x))为什么使用 ReLU?
- 非线性:引入非线性,增强表达能力
- 稀疏性:负值区域输出为 0,产生稀疏激活
- 计算高效:简单的阈值操作
- 梯度稳定:正区域梯度恒为 1,缓解梯度消失
2.2 第二层:主胶囊层(PrimaryCaps)
设计目标
PrimaryCaps 层是从标量到向量的转折点,将卷积特征重新组织为胶囊向量。
关键结构
python
class PrimaryCaps(nn.Module):
def __init__(self, num_capsules=8, in_channels=256, out_channels=32):
# 创建 8 个并行的卷积层
self.capsules = nn.ModuleList([
nn.Conv2d(in_channels=256, out_channels=32,
kernel_size=9, stride=2, padding=0)
for _ in range(num_capsules)])为什么是 8 个胶囊?
设计考量:
✓ 足够多的胶囊可以编码丰富的特征组合
✓ 每个胶囊学习不同的特征子空间
✓ 8 是 2 的幂次,便于 GPU 并行计算
✓ 实验验证:8 个胶囊在 MNIST 上表现良好维度变换过程
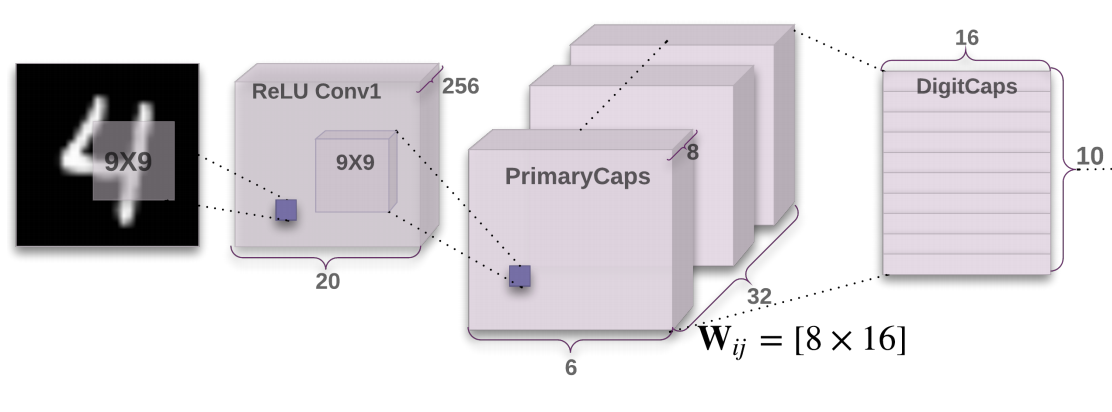
图 2:编码器架构示意图(来源:原论文)
这张图清晰地展示了编码器的三层结构:
- Conv1:256 个 9×9 卷积核,提取基础特征
- PrimaryCaps:8 个胶囊,每个输出 1152 维向量
- DigitCaps:10 个数字胶囊,每个输出 16 维向量
步骤 4 Squash
步骤 3 堆叠
步骤 2 重塑
步骤 1 卷积
32@9×9 stride=2
展平
8 个胶囊
squash 函数
20×20×256
6×6×32
1152×1
1152×8
1152×8
归一化向量
Squash 函数实现
python
def squash(tensor, dim=-1):
# 计算向量模长的平方
squared_norm = (tensor ** 2).sum(dim=dim, keepdim=True)
# 计算缩放因子:scale = ||v||² / (1 + ||v||²)
scale = squared_norm / (1.0 + squared_norm)
# 归一化向量:v_normalized = v / ||v||
normalized = tensor / torch.sqrt(squared_norm + 1e-9)
# 应用缩放:v_output = scale * v_normalized
return scale * normalizedSquash 函数的几何意义
很小≈0
很大
输入向量 v
计算模长||v||
输出接近 0
特征不存在
输出接近 1
特征存在
方向保持不变
模长在 0-1 区间
2.3 第三层:数字胶囊层(DigitCaps)
设计目标
DigitCaps 层是编码器的最高层,每个胶囊对应一个数字类别(0-9)。
关键特性
python
class DigitCaps(nn.Module):
def __init__(self, in_caps=8, in_dim=1152, out_caps=10, out_dim=16):
# 可学习的路由权重矩阵
self.weight = nn.Parameter(torch.randn(1, out_caps, in_caps, out_dim, in_dim))核心参数
| 参数 | 值 | 含义 |
|---|---|---|
in_caps |
8 | 输入胶囊数量(PrimaryCaps 的输出) |
in_dim |
1152 | 每个输入胶囊的维度 |
out_caps |
10 | 输出胶囊数量(对应 0-9) |
out_dim |
16 | 每个输出胶囊的维度 |
路由机制概览
PrimaryCaps (8 个胶囊)
↓
动态路由 (3 次迭代)
↓
DigitCaps (10 个胶囊)
每个 DigitCaps 接收来自所有 PrimaryCaps 的加权输入
权重通过动态路由算法迭代更新16 维向量的意义
DigitCaps 输出的 16 维向量编码了:
- v[0:2]: 位置信息(x, y 坐标)
- v[2:4]: 尺寸信息(宽,高)
- v[4:6]: 旋转角度
- v[6:8]: 笔画粗细
- v[8:15]: 其他变形参数
向量的模长表示"是该数字"的概率3. 解码器设计
3.1 解码器的作用
解码器有两个核心功能:
- 正则化编码器:通过重建任务迫使编码器保留更多信息
- 可视化验证:通过重建质量评估胶囊的表示能力
3.2 网络结构
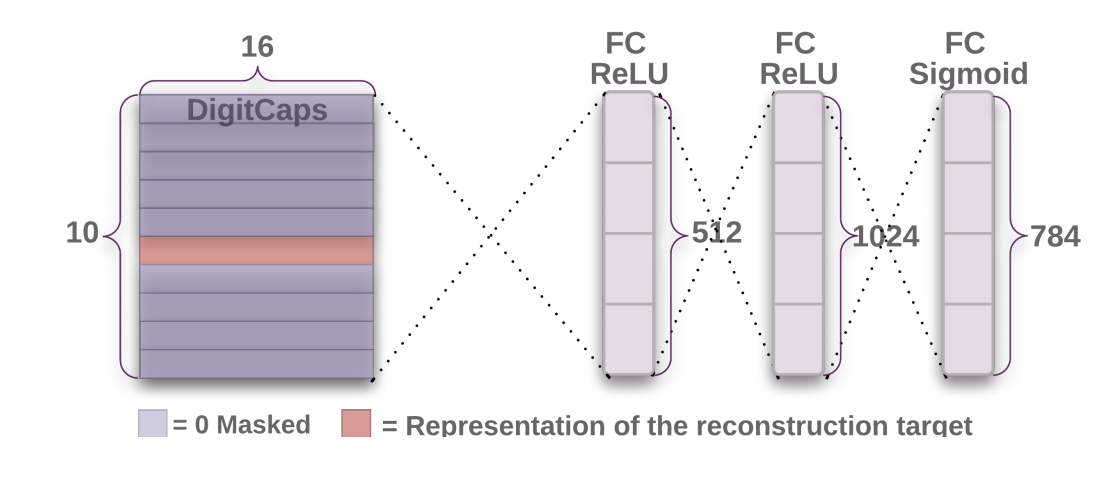
图 3:解码器架构示意图(来源:原论文)
解码器的工作流程:
- 掩码选择:选择模长最大的胶囊(预测类别)
- 展平:将 10×16 向量展平为 160 维
- 全连接层:三层全连接逐步恢复维度
- 重建输出:生成 28×28 的重建图像
python
class Decoder(nn.Module):
def __init__(self):
self.fc1 = nn.Linear(160, 512) # 160 = 10 个胶囊 × 16 维
self.fc2 = nn.Linear(512, 1024)
self.fc3 = nn.Linear(1024, 784) # 784 = 28×283.3 维度变换
输入:10 个 16 维向量 → 展平为 160 维
FC1: 160 → 512
ReLU 激活
FC2: 512 → 1024
ReLU 激活
FC3: 1024 → 784
Sigmoid 激活(输出像素值在 [0, 1])
输出:784 维 → 重塑为 28×28 图像3.4 掩码机制
训练时掩码
python
# 使用真实标签选择对应的胶囊
mask = torch.zeros_like(capsules_output)
mask[range(batch_size), labels] = 1
masked_output = capsules_output * mask推理时掩码
python
# 选择模长最大的胶囊
lengths = torch.norm(capsules_output, dim=-1)
max_length_idx = torch.argmax(lengths, dim=-1)
mask = torch.zeros_like(capsules_output)
mask[range(batch_size), max_length_idx] = 1
masked_output = capsules_output * mask3.5 重建损失的作用
总损失 = 分类损失 + 0.0005 × 重建损失
重建损失的意义:
✓ 迫使胶囊编码更多视觉信息
✓ 防止过拟合
✓ 提高泛化能力
✓ 提供可解释性4. 数据流分析
4.1 前向传播完整流程
Step 1: 输入图像
形状:[batch_size, 1, 28, 28]
含义:一批 28×28 灰度图像
↓
Step 2: ConvLayer
操作:Conv2d(1→256, 9×9) + ReLU
形状:[batch_size, 256, 20, 20]
含义:256 个 20×20 特征图
↓
Step 3: PrimaryCaps
操作:8 个 Conv2d(256→32, 9×9, stride=2) + Squash
形状:[batch_size, 1152, 8]
含义:8 个 1152 维胶囊向量
↓
Step 4: DigitCaps
操作:动态路由(3 次迭代)+ Squash
形状:[batch_size, 10, 16]
含义:10 个 16 维数字胶囊
↓
Step 5: 分类输出
操作:计算 10 个胶囊的模长
形状:[batch_size, 10]
含义:每个数字的概率
↓
Step 6: 解码器输入
操作:掩码选择 + 展平
形状:[batch_size, 160]
含义:选中的胶囊向量
↓
Step 7: Decoder
操作:FC1(512) → FC2(1024) → FC3(784)
形状:[batch_size, 784]
含义:重建的图像像素
↓
Step 8: 重建图像
形状:[batch_size, 1, 28, 28]
含义:重建的 28×28 图像4.2 梯度反向传播
损失函数
↓
分类损失(Margin Loss)
重建损失(MSE Loss)
↓
梯度流向 Decoder
↓
梯度流向 DigitCaps
↓
梯度流向 PrimaryCaps
↓
梯度流向 ConvLayer5. 设计哲学
5.1 层次化表示
设计原则:从具体到抽象
像素级 (Pixel Level)
↓ 28×28 原始像素
特征级 (Feature Level)
↓ 256 个卷积特征
部件级 (Part Level)
↓ 8 个主胶囊
对象级 (Object Level)
↓ 10 个数字胶囊5.2 信息瓶颈
信息流:
28×28 = 784 像素
↓ 压缩
20×20×256 = 102,400 特征
↓ 选择
1152×8 = 9,216 维
↓ 抽象
16×10 = 160 维
↓ 重建
784 像素
瓶颈处的 160 维编码了最本质的特征5.3 端到端训练
优势:
✓ 所有参数联合优化
✓ 特征表示自学习
✓ 无需人工设计特征
✓ 适应数据分布5.4 可解释性设计
可解释性体现:
1. 胶囊向量模长 → 存在概率
2. 胶囊向量方向 → 姿态参数
3. 解码器重建 → 可视化验证
4. 动态路由权重 → 注意力分布6. 总结
架构设计要点
| 层级 | 核心创新 | 技术要点 |
|---|---|---|
| ConvLayer | 特征提取 | 大卷积核、多通道 |
| PrimaryCaps | 标量→向量 | 并行卷积、Squash |
| DigitCaps | 动态路由 | 迭代路由、类别表示 |
| Decoder | 重建验证 | 全连接、掩码机制 |
设计亮点
✓ 层次化编码 :从像素到语义的渐进抽象
✓ 向量表示 :同时编码存在性和姿态
✓ 动态路由 :自适应的特征组合
✓ 重建监督:双重任务提升泛化