js 实现归并排序算法

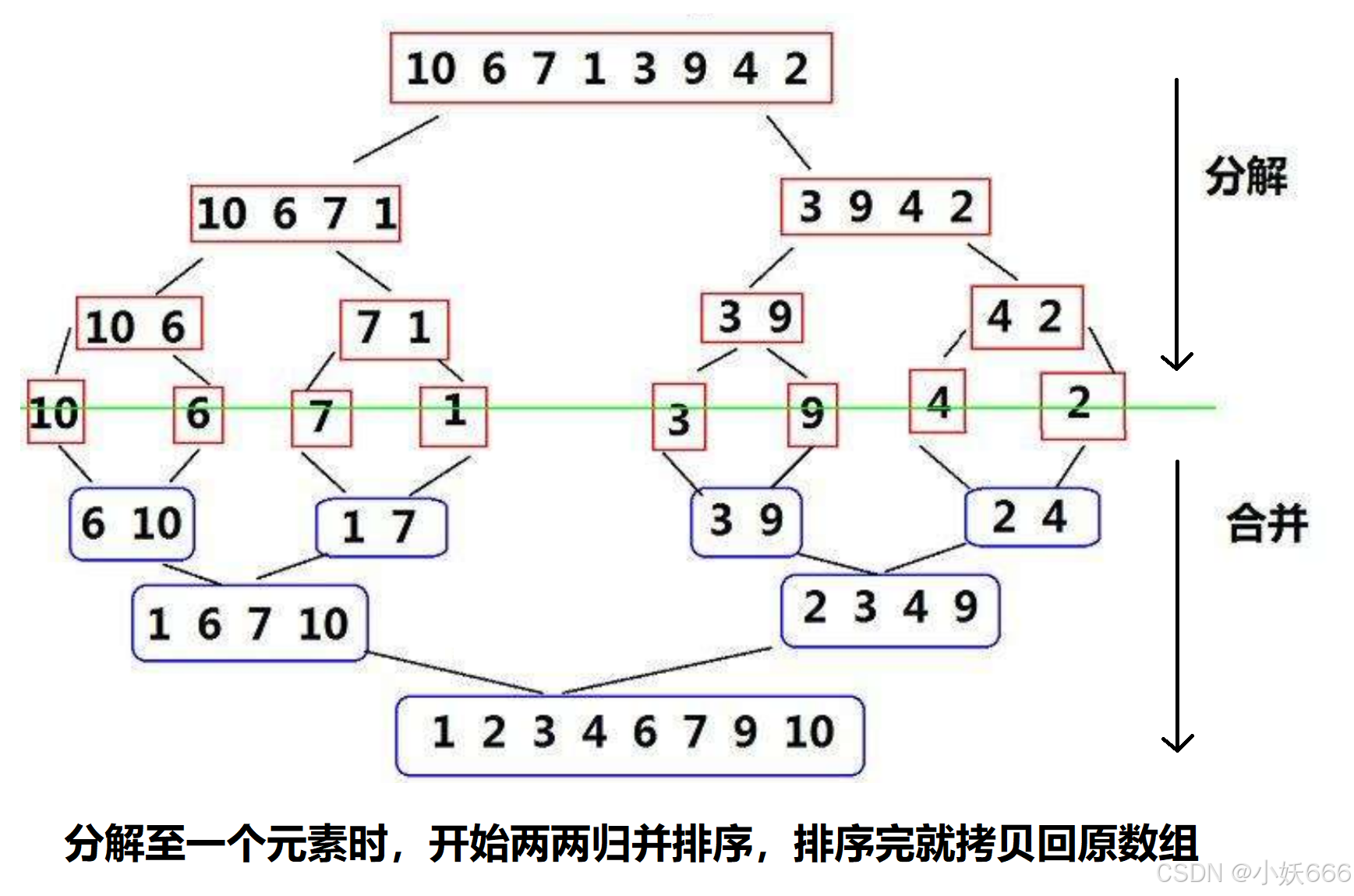
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

递归法求解

javascript 复制代码

const mergeSort = (arr) => {
    const n = arr.length
    if (n <= 1) {
        return arr
    }
    let mid = Math.floor(n / 2)
    const arr1 = arr.slice(0, mid)
    const arr2 = arr.slice(mid, n)
    return merge(mergeSort(arr1), mergeSort(arr2), n)
}

const merge = (arr1, arr2, n) => {
    const mergeArr = new Array(n)
    let idx = 0
    let idx1 = 0
    let idx2 = 0
    while(idx1 < arr1.length && idx2 < arr2.length) {
        if (arr1[idx1] < arr2[idx2]) {
            mergeArr[idx] = arr1[idx1]
            idx1 += 1
        } else {
            mergeArr[idx] = arr2[idx2]
            idx2 += 1
        }
        idx += 1
    }
    if (idx1 < arr1.length) {
        while(idx1 < arr1.length) {
            mergeArr[idx] = arr1[idx1]
            idx1 += 1
            idx += 1
        }
    } else {
        while(idx2 < arr2.length) {
            mergeArr[idx] = arr2[idx2]
            idx2 += 1
            idx += 1
        }
    }
    return mergeArr
}

const arr = [1100,200,500,1600,25,13,685,23651,0,12,35,478,66,5,3,9,8,456,58,68,95,25,12,45,65,8,78,95,68,321,456,122,258,951,864,57,85,95,96,93,92,94,98,25,26,28,29,68,65,62,67,789,752,751,745,6859,3,20,359,215,687,592]
const newarr = mergeSort(arr)
console.log(newarr)

递归法需要新建很多新数组占用存储空间，数据大时比较占内存。

非递归法

gap从小往大逐渐增加，c++的实现方法如下

cpp 复制代码

// 非递归 处理越界版本
void _MergeSort(int* a, int L, int R, int* tmp, int n) {
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = begin1 + gap - 1;
			int begin2 = end1 + 1, end2 = begin2 + gap - 1;

			// 处理越界的逻辑
			if (end1 >= n || begin2 >= n) break;
			if(end2 >= n) end2 = n - 1;


			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2) {
				if (a[begin1] < a[begin2]) {
					tmp[j++] = a[begin1++];
				}
				else if (a[begin1] >= a[begin2]) { // 还有一种相等的情况，随便加在一个地方就行
					tmp[j++] = a[begin2++];
				}
			}

			// 当区间没走完，就把剩下的拷贝进数组
			while (begin1 <= end1) {
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2) {
				tmp[j++] = a[begin2++];
			}
			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1)); // 注意不能直接用 begin1 ，begin1 已经加加变化过了
		}
		gap *= 2;
	}
}