《AT_arc081_d [ARC081F] Flip and Rectangles》

题目描述

有一个 H×W 的网格。网格中的每个格子被涂成黑色或白色。从上到下第 i 行，从左到右第 j 列的格子，如果 Si 的第 j 个字符是 #，那么该格子是黑色；如果是 .，那么是白色。

Sunnuke 君可以任意次数地进行如下操作：

任选网格中的某一行或某一列，将该行或该列的所有格子的颜色反转（即，将黑色格子变成白色，将白色格子变成黑色）。

在操作结束后，Sunnuke 君会选择网格中的一个长方形。此时，所选长方形中的所有格子必须都是黑色。

若操作合理，Sunnuke 君能选择的长方形的最大面积是多少？

输入格式

输入以如下格式从标准输入中给出。

H W

S1

S2

⋮

SH

输出格式

输出 Sunnuke 君能选择的最大长方形的面积。

显示翻译

题意翻译

输入输出样例

输入 #1复制

复制代码

3 3
..#
##.
.#.

输出 #1复制

复制代码

输入 #2复制

复制代码

4 4
....
....
....
....

输出 #2复制

复制代码

输入 #3复制

复制代码

10 8
##...#.#
##...#.#
..###.#.
#.##.#.#
.#..#.#.
..##.#.#
##.#.#..
...#.#..
###.#.##
###..###

输出 #3复制

复制代码

说明/提示

限制条件

2≤H≤2000
2≤W≤2000
∣Si∣=W
Si 仅由 # 和 . 组成。

样例说明 1

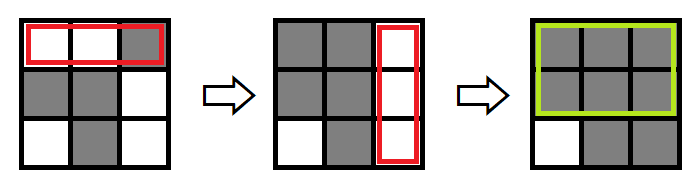
如图所示，如果将第 1 行和第 3 列进行反转，则可以选出一个 2×3 的长方形。

由 ChatGPT 5 翻译

代码实现：

cpp 复制代码

#include "iostream"
#include "cstdio"

#define N 2005

using namespace std;

int n,m,ans;
int L[N][N],R[N][N],h[N][N];
bool g[N][N];

int main()
{
    scanf("%d%d",&n,&m);
    ans=max(n,m);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            char c;
            cin>>c;
            if(c=='#')
                g[i][j]=true;
        }
    }
    n--;m--;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            g[i][j]=!((g[i][j]+g[i+1][j]+g[i][j+1]+g[i+1][j+1])&1);
            L[i][j]=R[i][j]=j;
        }
    for(int i=1;i<=n;i++)
        for(int j=2;j<=m;j++)
            if(g[i][j]&&g[i][j-1])
                L[i][j]=L[i][j-1];
    for(int i=1;i<=n;i++)
        for(int j=m-1;j;j--)
            if(g[i][j]&&g[i][j+1])
                R[i][j]=R[i][j+1];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(g[i][j])
                h[i][j]=h[i-1][j]+1;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            if(g[i][j]&&g[i-1][j])
            {
                L[i][j]=max(L[i][j],L[i-1][j]);
                R[i][j]=min(R[i][j],R[i-1][j]);
            }
            ans=max(ans,(R[i][j]-L[i][j]+2)*(h[i][j]+1));
        }
    printf("%d\n",ans);
    return 0;
}