目录
[3.1 伯努利分布](#3.1 伯努利分布)
[完整代码 + 可视化](#完整代码 + 可视化)
[3.2 贝塔分布](#3.2 贝塔分布)
[完整代码 + 可视化](#完整代码 + 可视化)
[3.3 分类分布](#3.3 分类分布)
[完整代码 + 可视化](#完整代码 + 可视化)
[3.4 狄利克雷分布](#3.4 狄利克雷分布)
[完整代码 + 可视化](#完整代码 + 可视化)
[3.5 一元正态分布](#3.5 一元正态分布)
[完整代码 + 可视化](#完整代码 + 可视化)
[3.6 正态逆伽马分布](#3.6 正态逆伽马分布)
[完整代码 + 可视化](#完整代码 + 可视化)
[3.7 多元正态分布](#3.7 多元正态分布)
[完整代码 + 可视化(2D 案例)](#完整代码 + 可视化(2D 案例))
[3.8 正态逆维希特分布](#3.8 正态逆维希特分布)
[完整代码 + 可视化(2D 案例)](#完整代码 + 可视化(2D 案例))
[3.9 共轭性](#3.9 共轭性)
[完整代码(伯努利 + 贝塔共轭案例)](#完整代码(伯努利 + 贝塔共轭案例))
前言

大家好!今天我们来拆解《计算机视觉:模型、学习和推理》这本书的第 3 章 ------ 常用概率分布。概率分布是计算机视觉的数学基石,不管是图像分类、目标检测还是图像生成,都离不开这些分布的身影。
我会用通俗易懂的语言讲解核心概念(少公式、多比喻),每个知识点都配上可直接运行的 Python 完整代码 和可视化对比图(适配 Mac 系统中文显示),帮你直观理解这些分布的特点和应用场景。
3.1 伯努利分布

核心概念
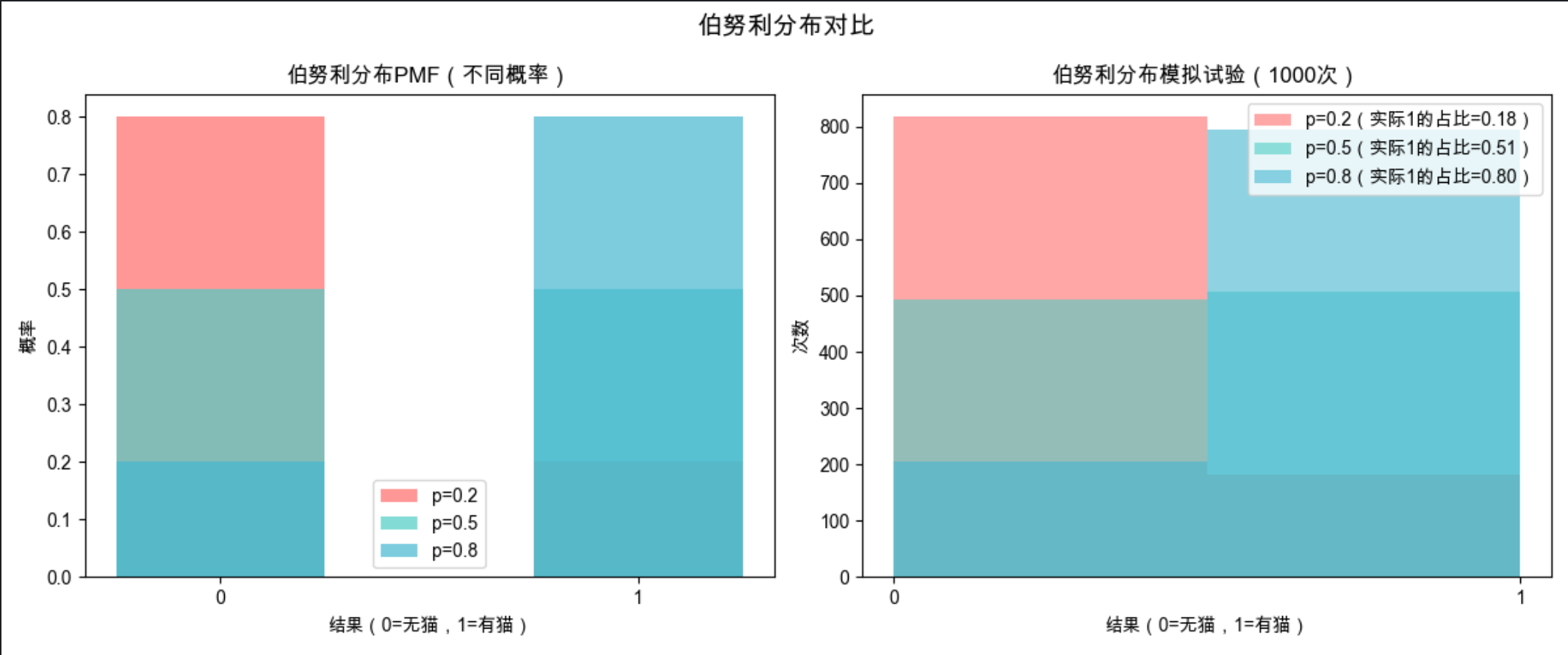
伯努利分布就像 "抛一次硬币":只有两种结果(正面 / 反面,对应 1/0),每次试验的结果互不影响,且某一结果的概率固定。比如 "判断图像中是否有猫"------ 有(1)或没有(0),就是典型的伯努利场景。
完整代码 + 可视化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 定义伯努利分布参数:p为出现1的概率
p_list = [0.2, 0.5, 0.8] # 三种不同概率(比如"图像中有猫"的概率)
colors = ['#FF6B6B', '#4ECDC4', '#45B7D1']
# 2. 创建画布
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
fig.suptitle('伯努利分布对比', fontsize=14, fontweight='bold')
# 3. 绘制概率质量函数(PMF)
x = [0, 1] # 伯努利分布只有0/1两个结果
for i, p in enumerate(p_list):
# 计算0和1对应的概率
pmf = [1-p, p]
ax1.bar(x, pmf, color=colors[i], alpha=0.7, label=f'p={p}', width=0.5)
ax1.set_title('伯努利分布PMF(不同概率)', fontsize=12)
ax1.set_xlabel('结果(0=无猫,1=有猫)')
ax1.set_ylabel('概率')
ax1.legend()
ax1.set_xticks(x)
# 4. 模拟试验:每个概率下抛1000次"硬币"
for i, p in enumerate(p_list):
# 生成1000个伯努利分布样本
samples = bernoulli.rvs(p, size=1000)
# 统计1出现的次数
count_1 = np.sum(samples)
# 绘制样本分布直方图
ax2.hist(samples, bins=2, alpha=0.6, color=colors[i], label=f'p={p}(实际1的占比={count_1/1000:.2f})')
ax2.set_title('伯努利分布模拟试验(1000次)', fontsize=12)
ax2.set_xlabel('结果(0=无猫,1=有猫)')
ax2.set_ylabel('次数')
ax2.legend()
ax2.set_xticks(x)
plt.tight_layout()
plt.show()代码解释
bernoulli.rvs(p, size):生成指定概率 p、指定数量的伯努利分布随机样本;
左图是理论概率(PMF),右图是模拟试验的实际结果,能直观看到 "概率 p 越大,1 出现的次数越多";
配色和布局优化,方便对比不同 p 值的差异。
应用场景
计算机视觉中用于二分类基础判断:比如像素是否为前景、图像是否模糊、检测框是否包含目标等。
3.2 贝塔分布
核心概念
贝塔分布是 "伯努利分布的管家"------ 它不直接描述 "硬币正反",而是描述 "硬币正面概率 p 的分布"。比如你不知道 "图像中有猫" 的概率 p 是多少,贝塔分布可以帮你估计 p 的可能取值范围(比如 p 大概率在 0.4~0.6 之间)。
完整代码 + 可视化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
# Mac中文配置(复用,后续不再重复写)
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 定义贝塔分布参数(α, β):不同参数对应不同形状
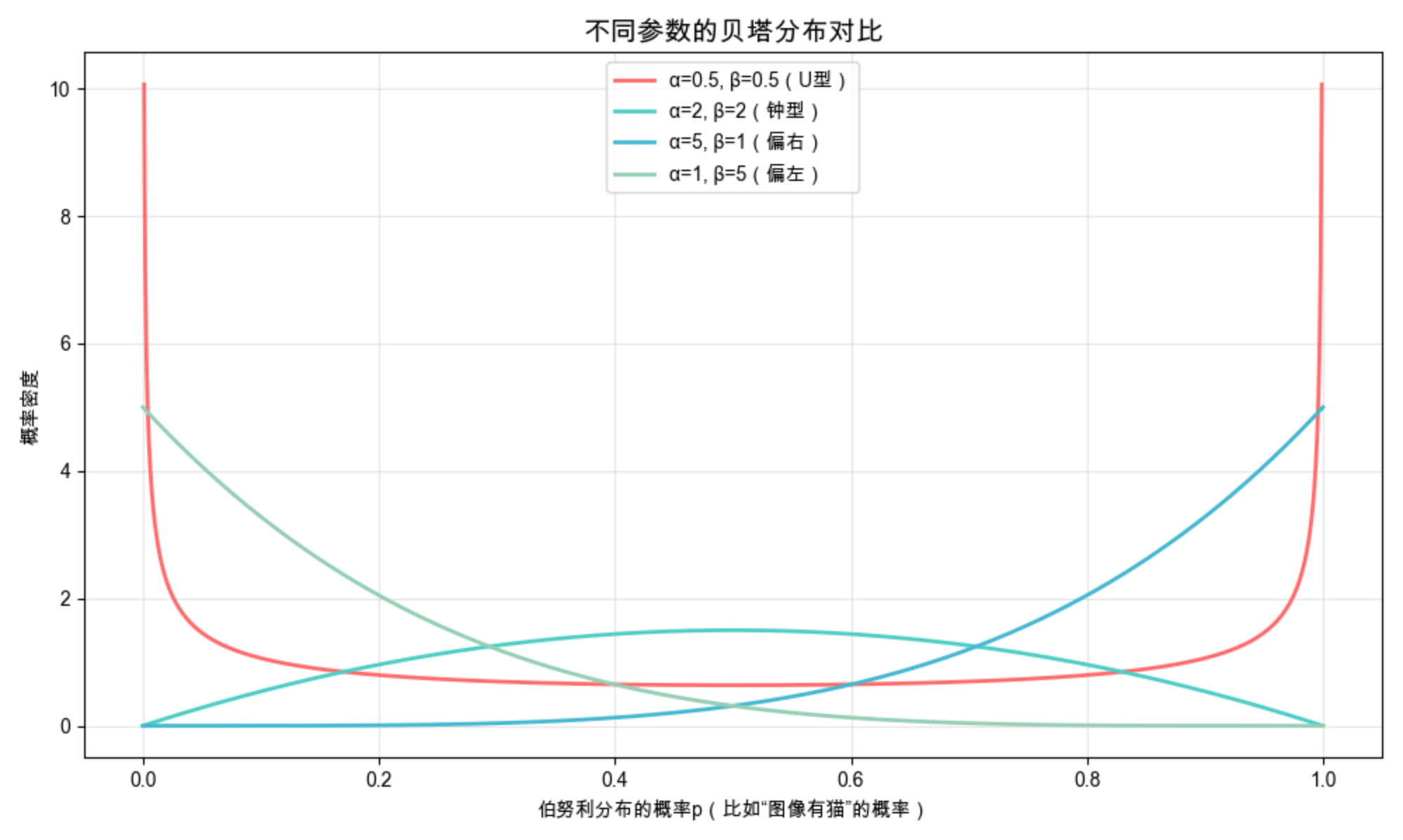
params_list = [(0.5, 0.5), (2, 2), (5, 1), (1, 5)]
labels = ['α=0.5, β=0.5(U型)', 'α=2, β=2(钟型)', 'α=5, β=1(偏右)', 'α=1, β=5(偏左)']
colors = ['#FF6B6B', '#4ECDC4', '#45B7D1', '#96CEB4']
# 2. 生成x轴数据(p的取值范围0~1)
x = np.linspace(0, 1, 1000)
# 3. 绘制贝塔分布概率密度函数(PDF)
fig, ax = plt.subplots(figsize=(10, 6))
ax.set_title('不同参数的贝塔分布对比', fontsize=14, fontweight='bold')
for i, (a, b) in enumerate(params_list):
# 计算PDF值
pdf = beta.pdf(x, a, b)
ax.plot(x, pdf, color=colors[i], label=labels[i], linewidth=2)
ax.set_xlabel('伯努利分布的概率p(比如"图像有猫"的概率)')
ax.set_ylabel('概率密度')
ax.legend()
ax.grid(alpha=0.3)
plt.tight_layout()
plt.show()代码解释
beta.pdf(x, a, b):计算贝塔分布在 x 处的概率密度;- α 和 β 的取值决定分布形状:α=β 时分布对称,α>β 时偏右,α<β 时偏左;
- 贝塔分布的取值范围固定为 0~1,刚好匹配概率 p 的范围。
应用场景
计算机视觉中用于二分类概率的先验估计 :比如在训练图像分类模型前,先用贝塔分布估计 "某类样本出现概率" 的先验范围。
3.3 分类分布
核心概念
分类分布是伯努利分布的 "升级版"------ 从 "二选一" 变成 "多选一"。比如 "图像分类(猫 / 狗 / 鸟 / 其他)",每个类别对应一个概率,所有类别概率之和为 1,就像 "掷骰子(6 个面)",每次只能出现一个结果。
完整代码 + 可视化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multinomial
# Mac中文配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 定义分类分布参数:3个类别(猫/狗/鸟)的概率
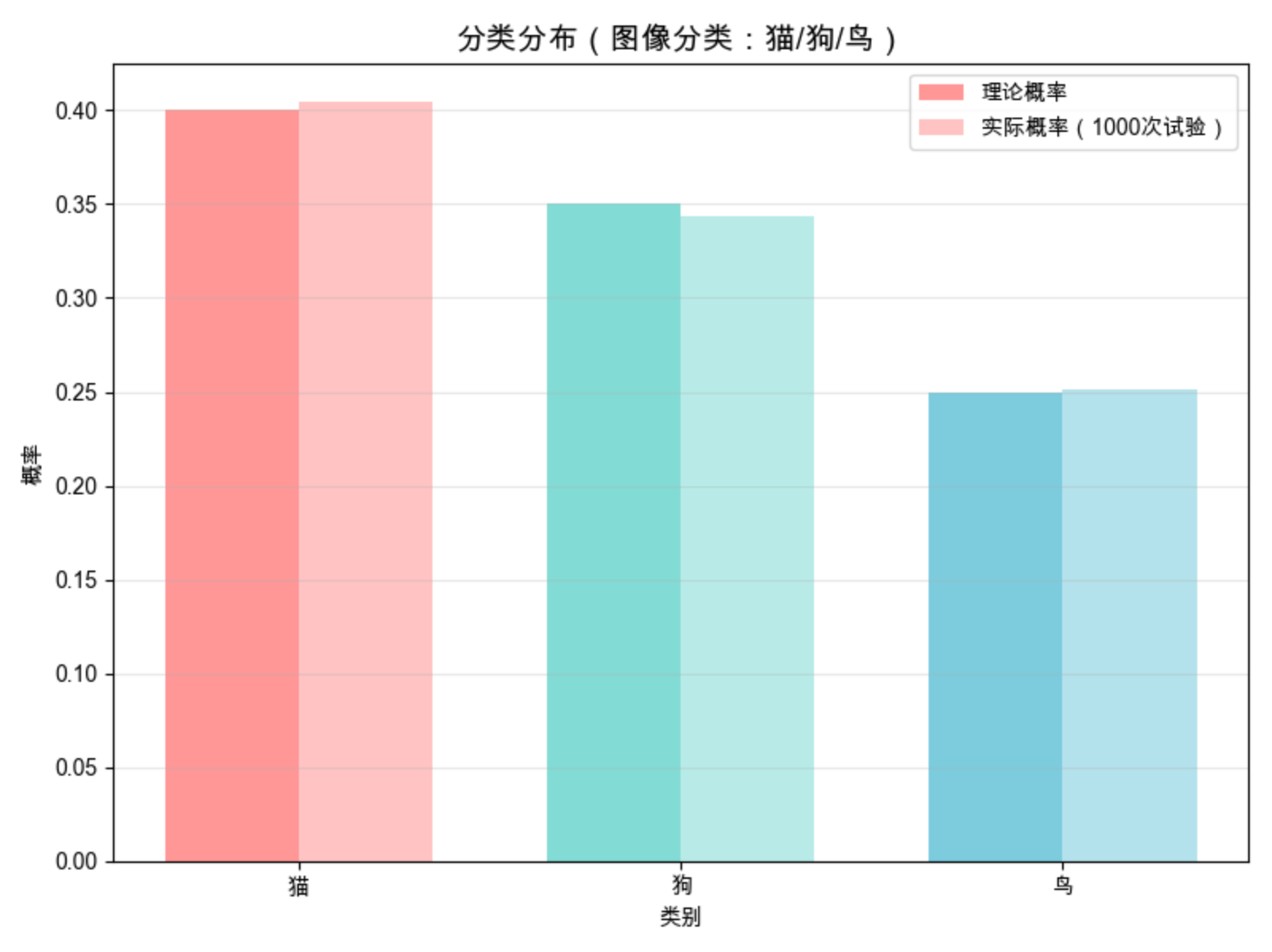
p_list = [0.4, 0.35, 0.25] # 概率和为1
categories = ['猫', '狗', '鸟']
colors = ['#FF6B6B', '#4ECDC4', '#45B7D1']
# 2. 模拟试验:1000次图像分类预测
n_trials = 1000
# 生成分类分布样本(n=1表示每次试验选1个类别,size=n_trials表示试验次数)
samples = multinomial.rvs(n=1, p=p_list, size=n_trials)
# 统计每个类别出现的次数(samples是二维数组,每行是[0,1,0]这样的形式)
counts = np.sum(samples, axis=0)
actual_p = counts / n_trials # 实际出现的概率
# 3. 绘制对比图:理论概率 vs 实际概率
fig, ax = plt.subplots(figsize=(8, 6))
x = np.arange(len(categories))
width = 0.35
# 绘制理论概率
ax.bar(x - width/2, p_list, width, label='理论概率', color=colors, alpha=0.7)
# 绘制实际概率
ax.bar(x + width/2, actual_p, width, label='实际概率(1000次试验)', color=colors, alpha=0.4)
ax.set_title('分类分布(图像分类:猫/狗/鸟)', fontsize=14, fontweight='bold')
ax.set_xlabel('类别')
ax.set_ylabel('概率')
ax.set_xticks(x)
ax.set_xticklabels(categories)
ax.legend()
ax.grid(alpha=0.3, axis='y')
plt.tight_layout()
plt.show()代码解释
multinomial.rvs(n=1, p=p_list, size):生成分类分布样本(n=1 表示每次选 1 类,对应图像分类的单标签场景);
对比理论概率和实际试验结果,能看到试验次数足够时,实际概率会逼近理论值;
核心特点:多类别、互斥、概率和为 1。
应用场景
计算机视觉核心场景 ------多分类任务 :比如图像分类(ImageNet 1000 类)、目标检测的类别预测、语义分割的像素分类等。
3.4 狄利克雷分布
核心概念
狄利克雷分布是 "分类分布的管家",就像贝塔分布对应伯努利分布一样,它描述 "分类分布中多个类别概率的联合分布"。比如你不知道 "猫 / 狗 / 鸟" 的分类概率分别是多少,狄利克雷分布可以帮你估计这一组概率的可能取值。
完整代码 + 可视化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import dirichlet
# Mac中文配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 定义狄利克雷分布参数(α1, α2, α3):对应猫/狗/鸟三个类别
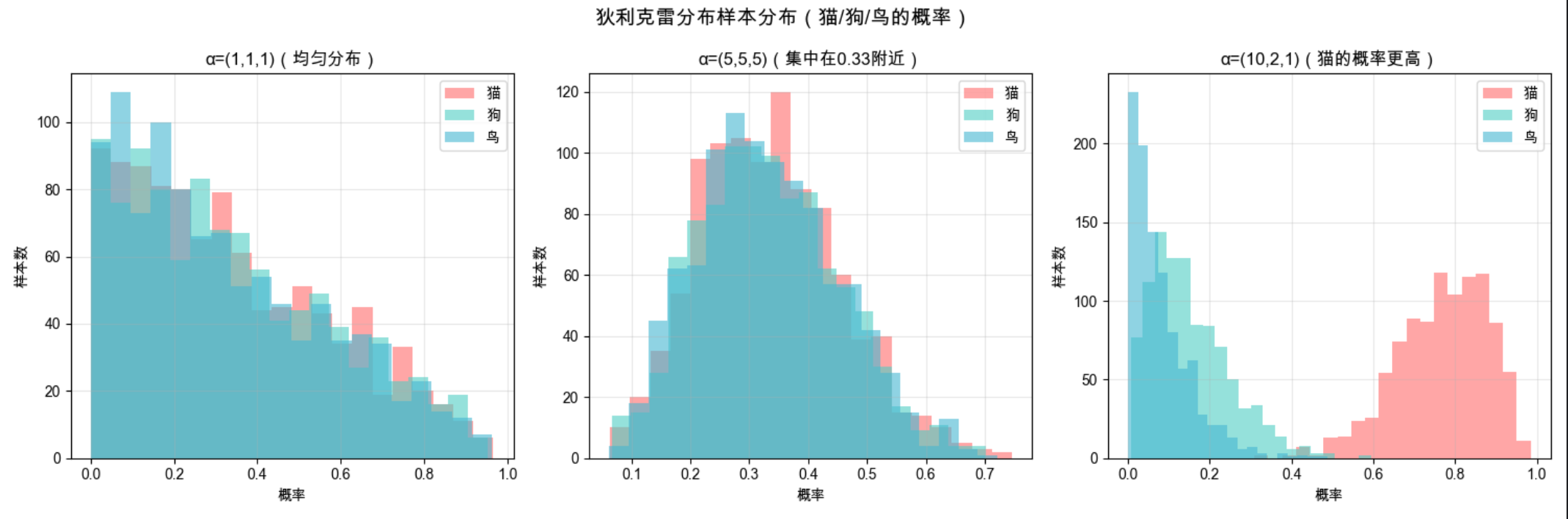
alpha_list = [(1, 1, 1), (5, 5, 5), (10, 2, 1)]
labels = ['α=(1,1,1)(均匀分布)', 'α=(5,5,5)(集中在0.33附近)', 'α=(10,2,1)(猫的概率更高)']
colors = ['#FF6B6B', '#4ECDC4', '#45B7D1']
# 2. 生成样本:每个参数生成1000个样本(每个样本是3个概率值,和为1)
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
fig.suptitle('狄利克雷分布样本分布(猫/狗/鸟的概率)', fontsize=14, fontweight='bold')
for i, alpha in enumerate(alpha_list):
# 生成1000个狄利克雷分布样本
samples = dirichlet.rvs(alpha, size=1000)
# 绘制每个类别的概率分布直方图
axes[i].hist(samples[:, 0], bins=20, alpha=0.6, color='#FF6B6B', label='猫')
axes[i].hist(samples[:, 1], bins=20, alpha=0.6, color='#4ECDC4', label='狗')
axes[i].hist(samples[:, 2], bins=20, alpha=0.6, color='#45B7D1', label='鸟')
axes[i].set_title(labels[i])
axes[i].set_xlabel('概率')
axes[i].set_ylabel('样本数')
axes[i].legend()
axes[i].grid(alpha=0.3)
plt.tight_layout()
plt.show()代码解释
dirichlet.rvs(alpha, size):生成狄利克雷分布样本,每个样本是长度为 3 的数组(对应 3 个类别的概率,和为 1);
α 参数越大,对应类别的概率越集中;α 全为 1 时,所有概率组合的可能性均等;
狄利克雷分布是贝塔分布在多分类场景的推广。
应用场景
计算机视觉中用于多分类概率的先验估计 :比如在小样本图像分类任务中,用狄利克雷分布作为类别概率的先验,提升模型泛化能力。
3.5 一元正态分布
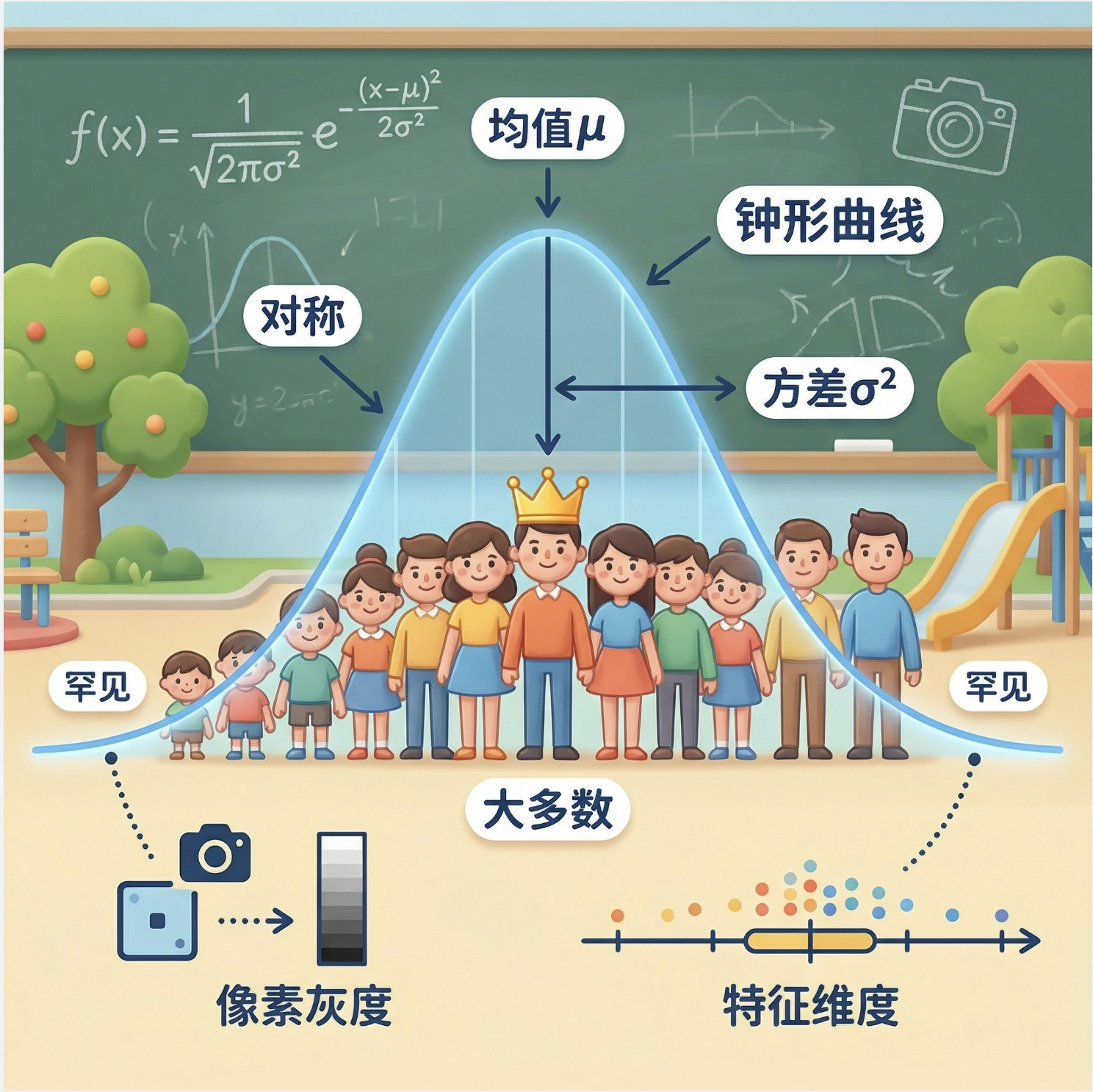
核心概念
一元正态分布(高斯分布)就像 "身高分布"------ 大多数值集中在平均值附近,离平均值越远,出现的概率越小,形状是对称的 "钟形曲线"。在计算机视觉中,单像素的灰度值、某类特征的单个维度值,通常都符合正态分布。
完整代码 + 可视化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Mac中文配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 定义不同参数的正态分布(μ=均值,σ=标准差)
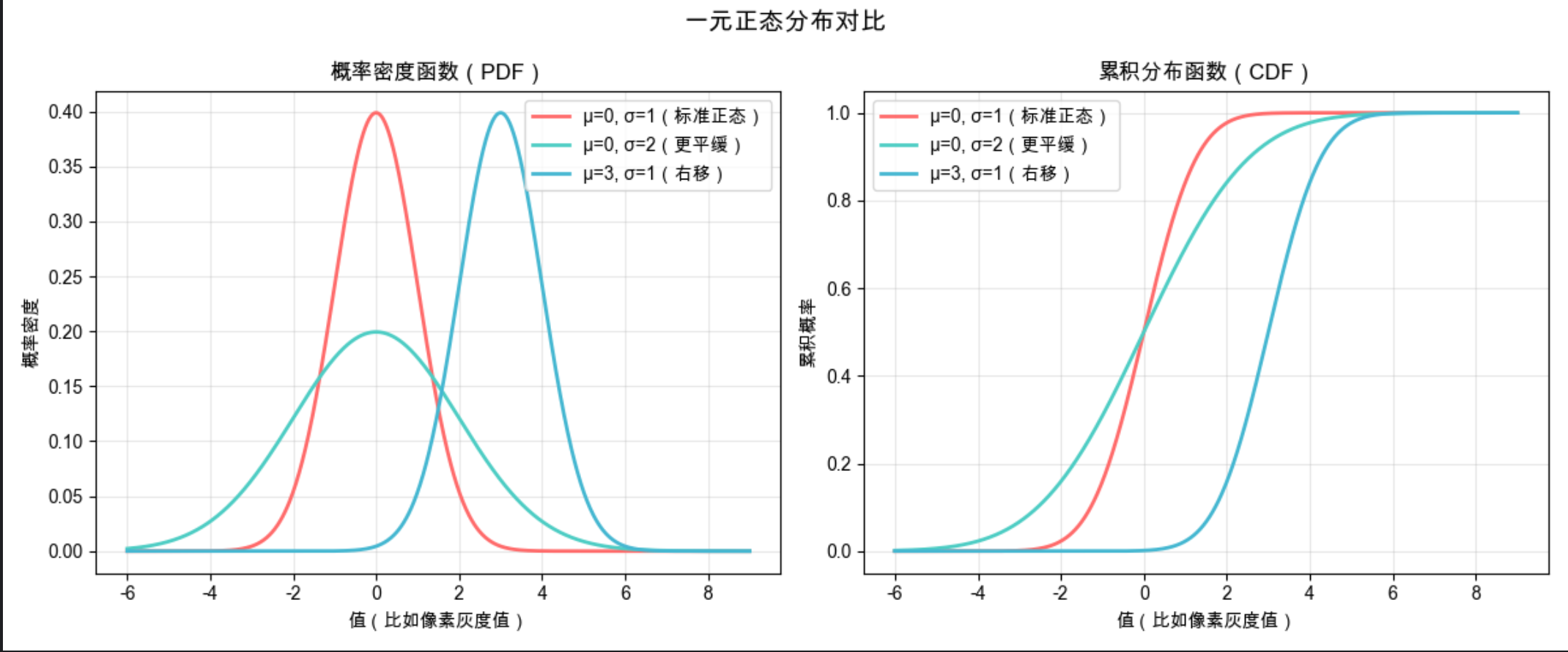
params_list = [(0, 1), (0, 2), (3, 1)]
labels = ['μ=0, σ=1(标准正态)', 'μ=0, σ=2(更平缓)', 'μ=3, σ=1(右移)']
colors = ['#FF6B6B', '#4ECDC4', '#45B7D1']
# 2. 生成x轴数据
x = np.linspace(-6, 9, 1000)
# 3. 绘制PDF和CDF对比
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
fig.suptitle('一元正态分布对比', fontsize=14, fontweight='bold')
# PDF(概率密度函数)
for i, (mu, sigma) in enumerate(params_list):
pdf = norm.pdf(x, mu, sigma)
ax1.plot(x, pdf, color=colors[i], label=labels[i], linewidth=2)
ax1.set_title('概率密度函数(PDF)', fontsize=12)
ax1.set_xlabel('值(比如像素灰度值)')
ax1.set_ylabel('概率密度')
ax1.legend()
ax1.grid(alpha=0.3)
# CDF(累积分布函数)
for i, (mu, sigma) in enumerate(params_list):
cdf = norm.cdf(x, mu, sigma)
ax2.plot(x, cdf, color=colors[i], label=labels[i], linewidth=2)
ax2.set_title('累积分布函数(CDF)', fontsize=12)
ax2.set_xlabel('值(比如像素灰度值)')
ax2.set_ylabel('累积概率')
ax2.legend()
ax2.grid(alpha=0.3)
plt.tight_layout()
plt.show()代码解释
norm.pdf(x, mu, sigma):计算正态分布在 x 处的概率密度;norm.cdf是累积概率;
μ 决定曲线的位置(左右移动),σ 决定曲线的 "胖瘦"(σ 越大,曲线越平缓,数据越分散);
标准正态分布是 μ=0、σ=1 的特殊情况。
应用场景
计算机视觉中用于单特征建模 :比如像素灰度值的分布拟合、图像噪声(高斯噪声)的生成、特征归一化(标准化)的基础。
3.6 正态逆伽马分布
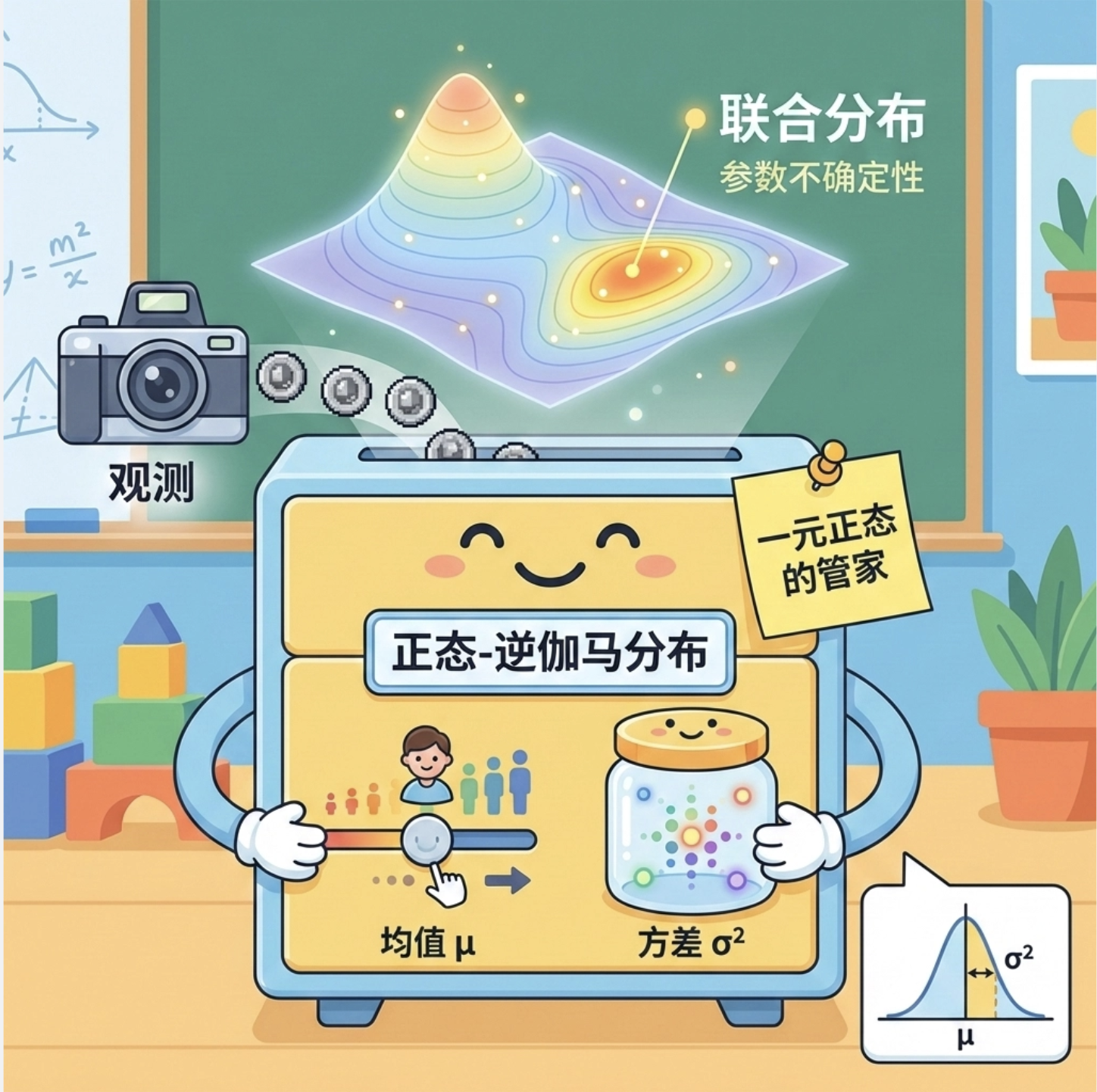
核心概念
正态逆伽马分布是 "一元正态分布的管家"------ 它同时描述正态分布的均值 μ 和方差 σ² 的联合分布。比如你不知道某像素灰度值的均值和方差是多少,正态逆伽马分布可以帮你估计这两个参数的可能取值范围。
完整代码 + 可视化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, invgamma
# Mac中文配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 定义正态逆伽马分布参数(α, β, μ0, λ)
alpha, beta = 5, 2 # 逆伽马分布参数(控制方差σ²)
mu0, lam = 0, 1 # 正态分布参数(控制均值μ)
# 2. 生成方差σ²的样本(逆伽马分布)
sigma2_samples = invgamma.rvs(alpha, scale=beta, size=1000)
# 3. 对每个σ²,生成均值μ的样本(正态分布)
mu_samples = norm.rvs(loc=mu0, scale=np.sqrt(sigma2_samples/lam), size=1000)
# 4. 绘制联合分布散点图+边际分布直方图
fig = plt.figure(figsize=(10, 8))
# 散点图(μ vs σ²)
ax_scatter = fig.add_subplot(221)
ax_scatter.scatter(mu_samples, sigma2_samples, alpha=0.3, color='#45B7D1')
ax_scatter.set_title('μ和σ²的联合分布', fontsize=12)
ax_scatter.set_xlabel('均值μ')
ax_scatter.set_ylabel('方差σ²')
ax_scatter.grid(alpha=0.3)
# μ的边际分布
ax_mu = fig.add_subplot(222)
ax_mu.hist(mu_samples, bins=30, color='#FF6B6B', alpha=0.7)
ax_mu.set_title('均值μ的边际分布', fontsize=12)
ax_mu.set_xlabel('μ')
ax_mu.set_ylabel('样本数')
ax_mu.grid(alpha=0.3)
# σ²的边际分布
ax_sigma2 = fig.add_subplot(223)
ax_sigma2.hist(sigma2_samples, bins=30, color='#4ECDC4', alpha=0.7)
ax_sigma2.set_title('方差σ²的边际分布', fontsize=12)
ax_sigma2.set_xlabel('σ²')
ax_sigma2.set_ylabel('样本数')
ax_sigma2.grid(alpha=0.3)
plt.tight_layout()
plt.show()代码解释
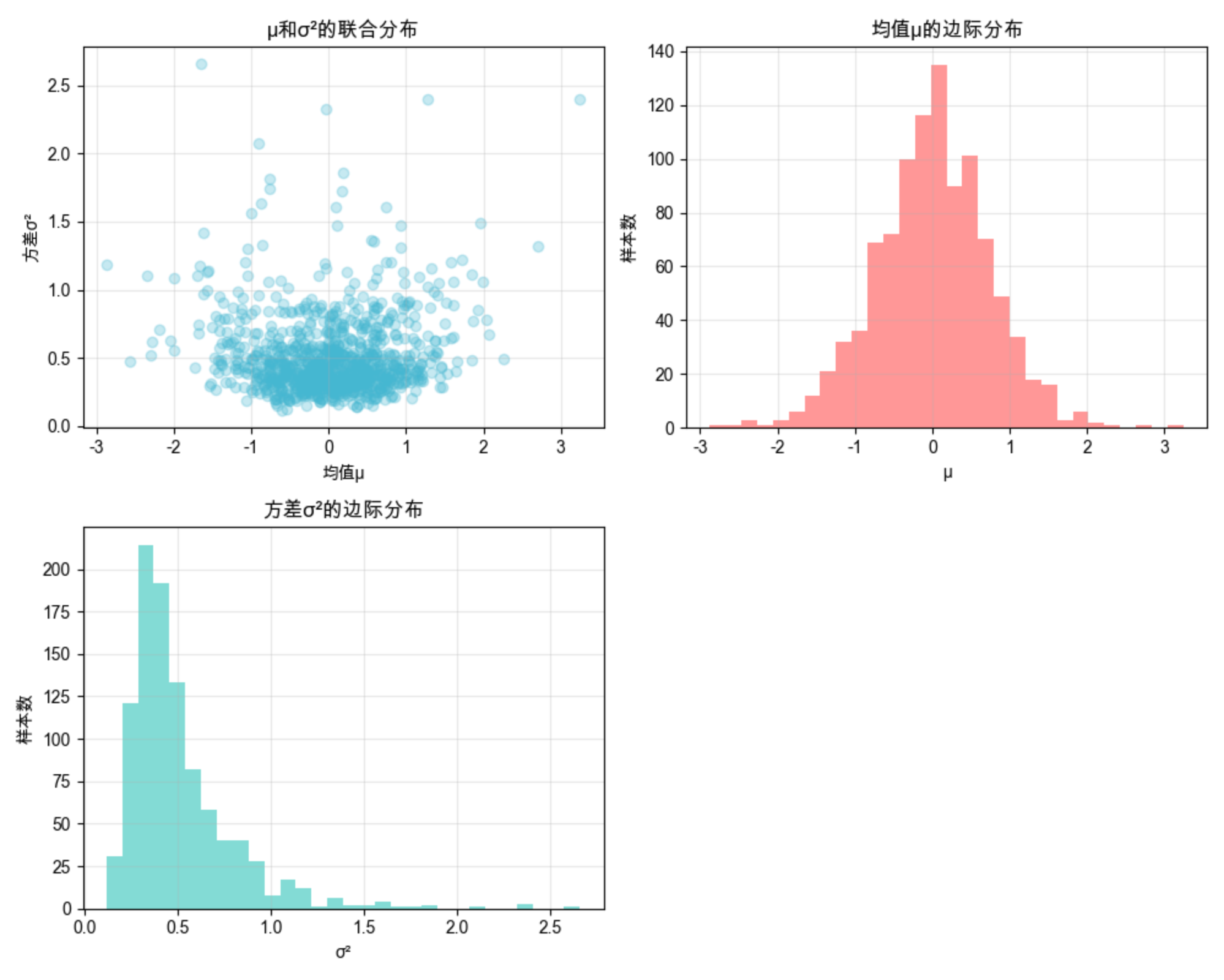
正态逆伽马分布由两部分组成:μ 服从正态分布(方差依赖 σ²),σ² 服从逆伽马分布;
invgamma.rvs(alpha, scale=beta):生成逆伽马分布样本(对应 σ²);
散点图能直观看到 μ 和 σ² 的联合分布关系,边际分布则展示单个参数的分布特点。
应用场景
计算机视觉中用于单特征参数的贝叶斯估计 :比如在图像去噪中,估计噪声的均值和方差,提升去噪效果。
3.7 多元正态分布
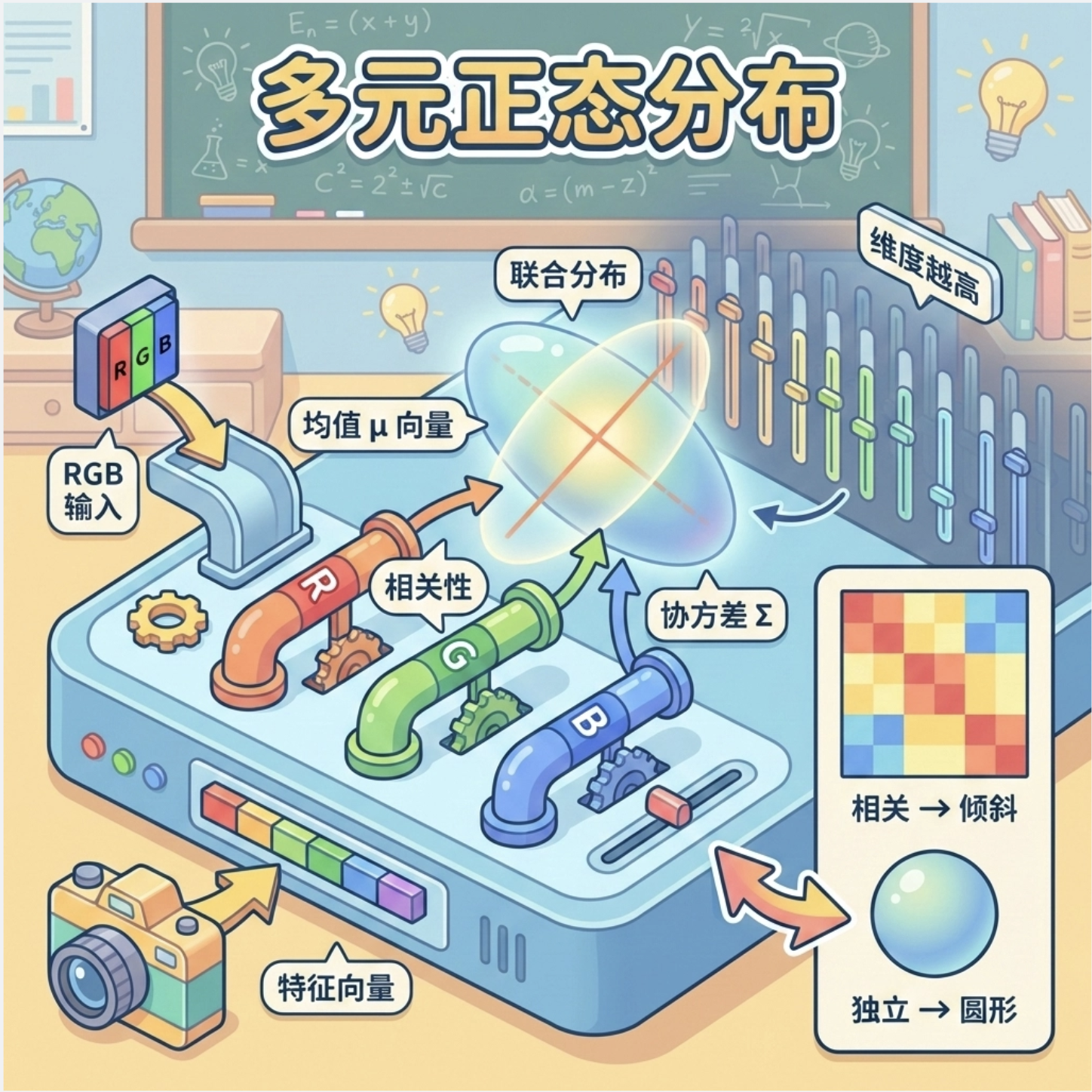
核心概念
多元正态分布是一元正态分布的 "多维版"------ 描述多个相关特征的联合分布。比如图像中一个像素的 RGB 三个通道值(3 维)、图像特征提取后的 128 维向量,都可以用多元正态分布建模,它不仅考虑每个维度的均值 / 方差,还考虑维度之间的相关性(比如 R 和 G 通道的相关性)。
完整代码 + 可视化(2D 案例)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
# Mac中文配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 定义2维正态分布参数(对应RGB的R和G通道)
# 案例1:无相关性(协方差矩阵对角元素非零,非对角为0)
mu1 = [50, 50] # 均值
cov1 = [[100, 0], [0, 100]] # 协方差矩阵(无相关性)
# 案例2:正相关性(非对角元素为正)
mu2 = [50, 50]
cov2 = [[100, 80], [80, 100]] # R和G正相关
# 案例3:负相关性(非对角元素为负)
mu3 = [50, 50]
cov3 = [[100, -80], [-80, 100]] # R和G负相关
# 2. 生成网格数据
x, y = np.meshgrid(np.linspace(20, 80, 100), np.linspace(20, 80, 100))
pos = np.dstack((x, y))
# 3. 绘制等高线图(直观展示分布形状)
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
fig.suptitle('2维正态分布(R/G通道值)', fontsize=14, fontweight='bold')
# 案例1
rv1 = multivariate_normal(mu1, cov1)
axes[0].contourf(x, y, rv1.pdf(pos), cmap='Blues', alpha=0.8)
axes[0].set_title('无相关性(协方差非对角=0)', fontsize=12)
axes[0].set_xlabel('R通道值')
axes[0].set_ylabel('G通道值')
# 案例2
rv2 = multivariate_normal(mu2, cov2)
axes[1].contourf(x, y, rv2.pdf(pos), cmap='Reds', alpha=0.8)
axes[1].set_title('正相关性(协方差非对角=80)', fontsize=12)
axes[1].set_xlabel('R通道值')
# 案例3
rv3 = multivariate_normal(mu3, cov3)
axes[2].contourf(x, y, rv3.pdf(pos), cmap='Greens', alpha=0.8)
axes[2].set_title('负相关性(协方差非对角=-80)', fontsize=12)
axes[2].set_xlabel('R通道值')
plt.tight_layout()
plt.show()代码解释
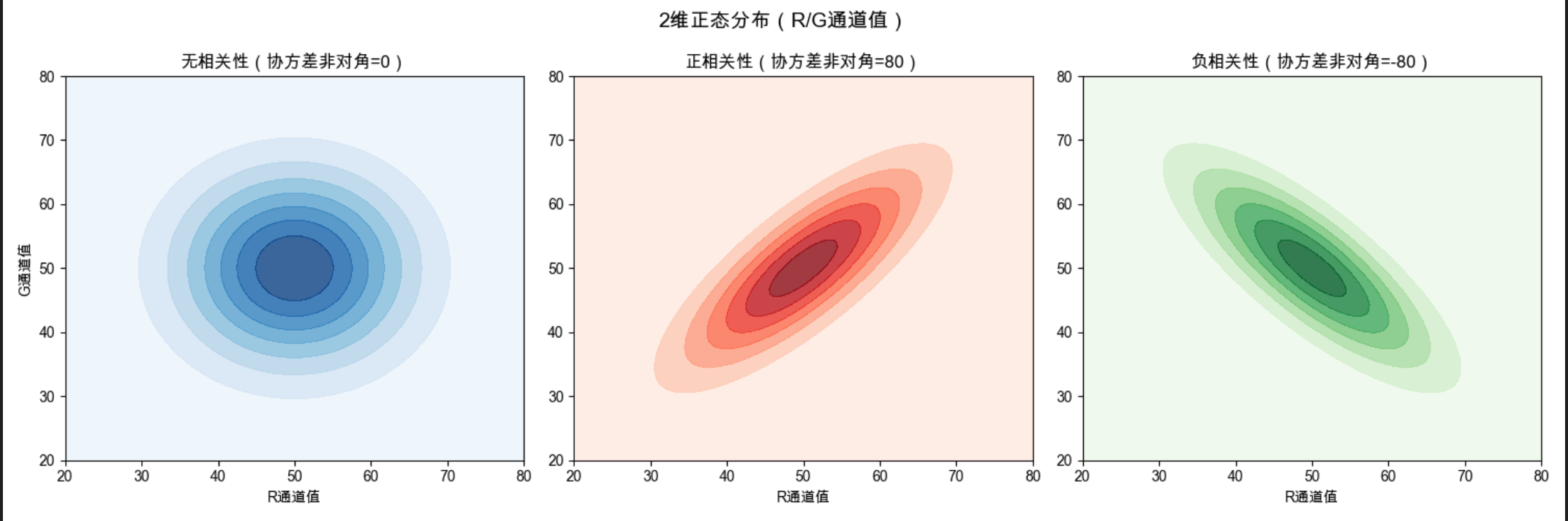
multivariate_normal(mu, cov):定义多元正态分布,mu 是均值向量,cov 是协方差矩阵;
协方差矩阵的非对角元素表示维度间的相关性:正 = 正相关,负 = 负相关,0 = 无相关;
等高线图的形状能直观反映相关性:无相关是圆形,正 / 负相关是椭圆形(方向不同)。
应用场景
计算机视觉核心场景 ------多维特征建模 :比如图像特征向量(CNN 输出)的分布、RGB 图像的颜色分布、人脸特征的降维与建模等。
3.8 正态逆维希特分布

核心概念
正态逆维希特分布是 "多元正态分布的管家"------ 它同时描述多元正态分布的均值向量 μ 和协方差矩阵 Σ 的联合分布。比如你不知道 RGB 三个通道值的均值向量和协方差矩阵,它可以帮你估计这两个参数的可能取值,是正态逆伽马分布在多维场景的推广。
完整代码 + 可视化(2D 案例)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal, invwishart
# Mac中文配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 定义正态逆维希特分布参数
nu = 4 # 逆维希特分布自由度(≥维度数,这里维度=2)
S = np.array([[100, 0], [0, 100]]) # 逆维希特分布尺度矩阵
mu0 = np.array([50, 50]) # 均值向量先验
lam = 1 # 精度参数
# 2. 生成协方差矩阵Σ的样本(逆维希特分布)
cov_samples = invwishart.rvs(df=nu, scale=S, size=100)
# 3. 对每个Σ,生成均值向量μ的样本(多元正态分布)
mu_samples = []
for cov in cov_samples:
mu = multivariate_normal.rvs(mean=mu0, cov=cov/lam)
mu_samples.append(mu)
mu_samples = np.array(mu_samples)
# 4. 可视化:μ的分布 + 随机选1个Σ的等高线
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
fig.suptitle('正态逆维希特分布(2D案例)', fontsize=14, fontweight='bold')
# μ向量的分布(散点图)
ax1.scatter(mu_samples[:, 0], mu_samples[:, 1], alpha=0.5, color='#45B7D1')
ax1.set_title('均值向量μ的分布', fontsize=12)
ax1.set_xlabel('μ1(R通道均值)')
ax1.set_ylabel('μ2(G通道均值)')
ax1.grid(alpha=0.3)
# 随机选1个Σ,绘制对应的多元正态分布等高线
random_cov = cov_samples[0]
x, y = np.meshgrid(np.linspace(40, 60, 100), np.linspace(40, 60, 100))
pos = np.dstack((x, y))
rv = multivariate_normal(mu0, random_cov)
ax2.contourf(x, y, rv.pdf(pos), cmap='Blues', alpha=0.8)
ax2.set_title(f'随机Σ的多元正态分布(Σ=\n{random_cov.round(2)})', fontsize=12)
ax2.set_xlabel('R通道值')
ax2.set_ylabel('G通道值')
plt.tight_layout()
plt.show()代码解释
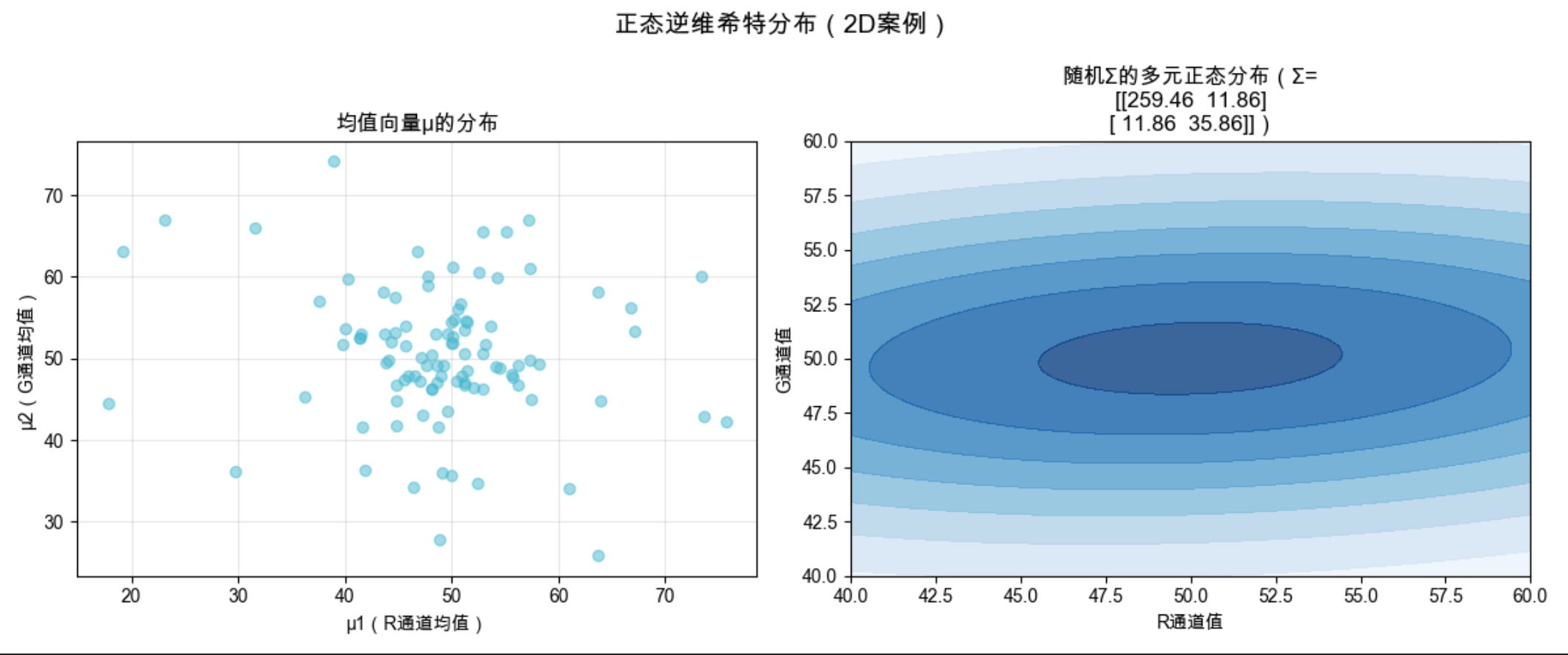
invwishart.rvs(df, scale):生成逆维希特分布样本(对应协方差矩阵 Σ);
对于每个 Σ 样本,μ 服从以 μ0 为均值、Σ/lam 为协方差的多元正态分布;
可视化展示了 μ 的分布,以及单个 Σ 对应的多元正态分布形状。
应用场景
计算机视觉中用于多维特征参数的贝叶斯估计 :比如在图像检索中,估计特征向量的均值和协方差矩阵,提升检索准确率。
3.9 共轭性
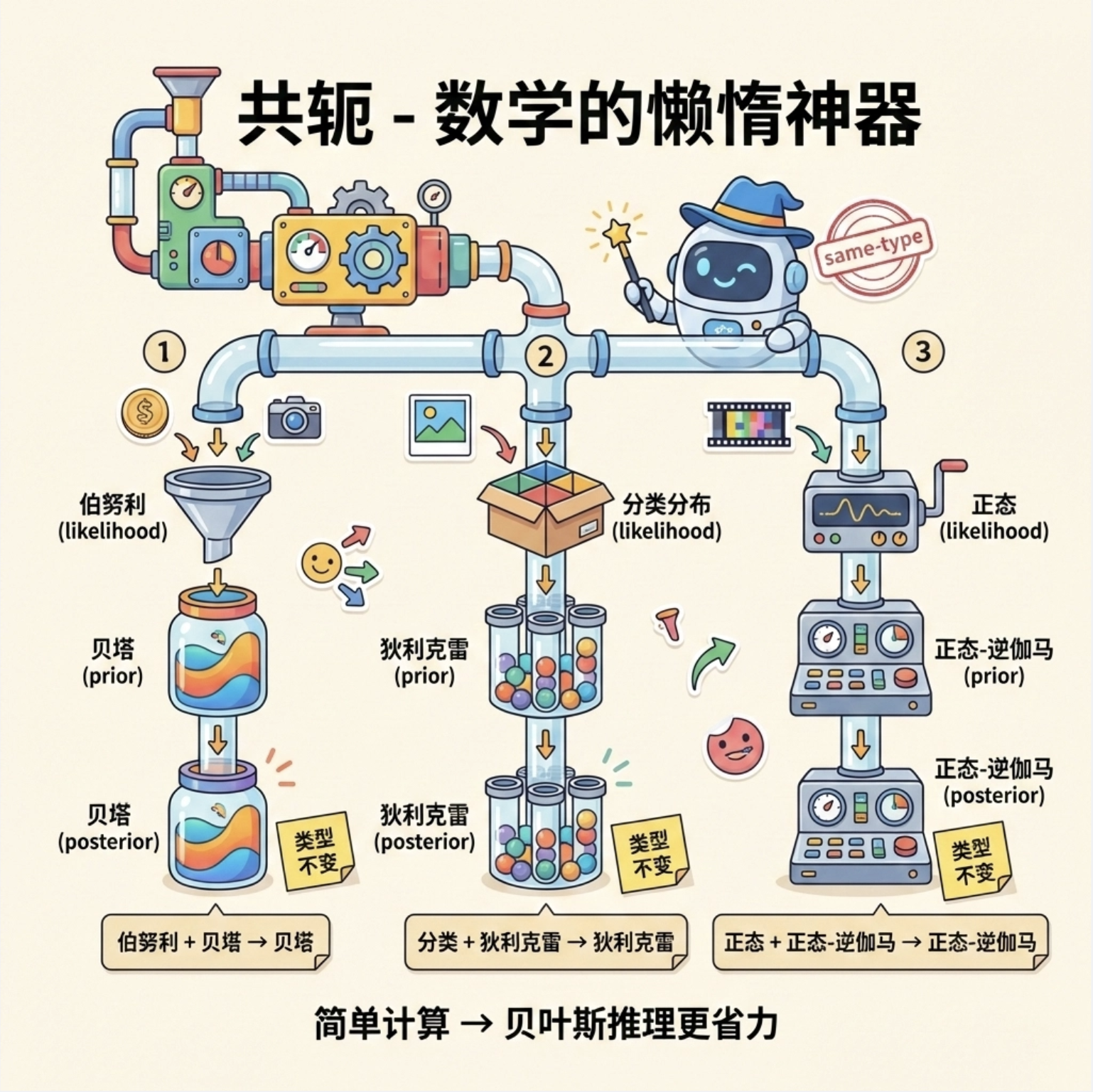
核心概念
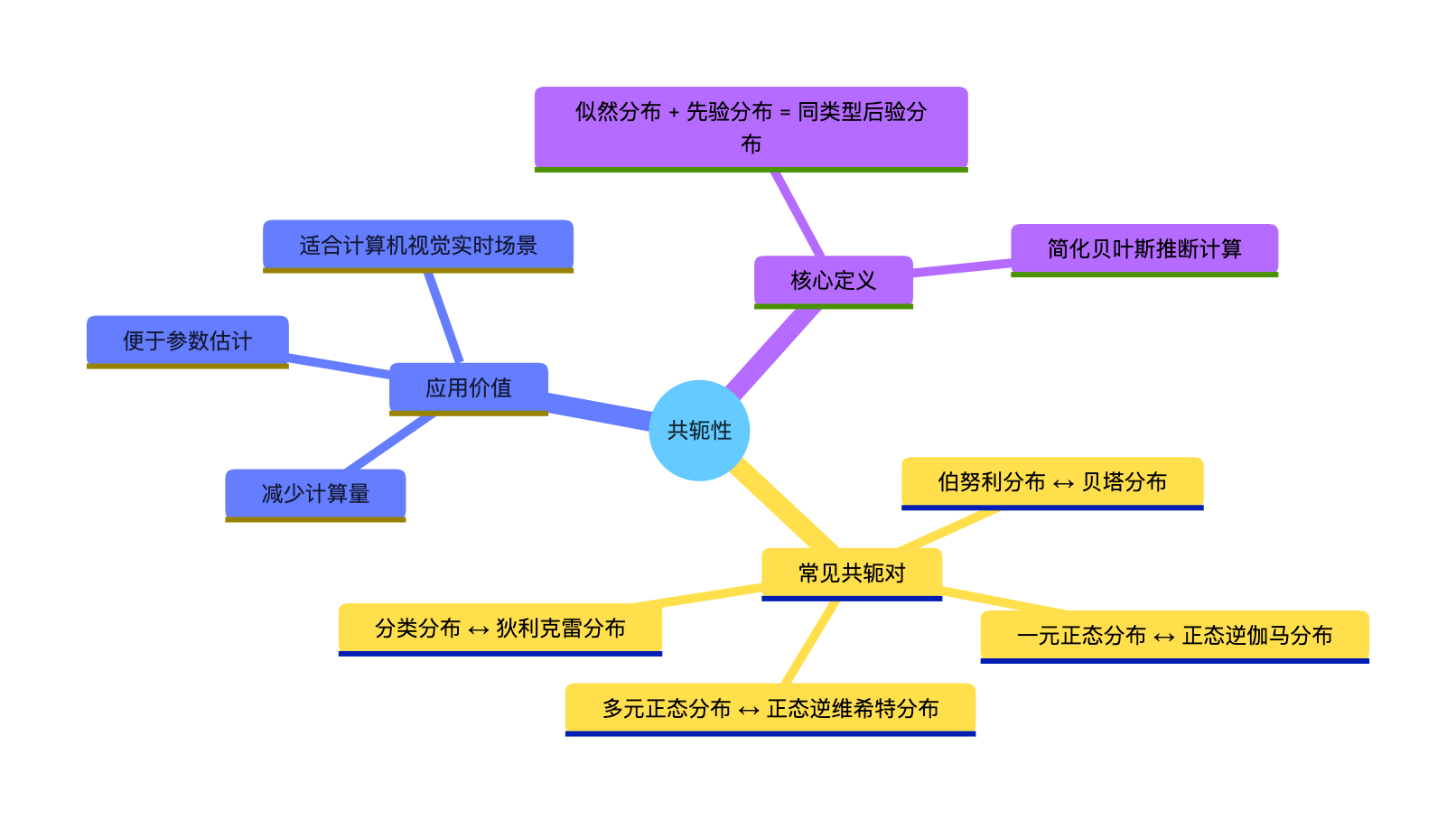
共轭性就像 "数学里的懒人神器"------ 如果先验分布和似然分布是 "共轭对",那么后验分布和先验分布是同一个类型的分布。比如:
- 伯努利分布(似然) + 贝塔分布(先验) → 贝塔分布(后验)
- 分类分布(似然) + 狄利克雷分布(先验) → 狄利克雷分布(后验)
- 正态分布(似然) + 正态逆伽马分布(先验) → 正态逆伽马分布(后验)
简单说:共轭性让后验分布的计算 "不换类型",大大简化贝叶斯推断的过程。
思维导图
完整代码(伯努利 + 贝塔共轭案例)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import bernoulli, beta
# Mac中文配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 1. 定义先验:贝塔分布α=2, β=2
alpha_prior, beta_prior = 2, 2
# 2. 生成似然数据:伯努利分布p=0.6,100个样本
p_true = 0.6
samples = bernoulli.rvs(p_true, size=100)
n_success = np.sum(samples) # 成功(1)的次数
n_failure = len(samples) - n_success # 失败(0)的次数
# 3. 后验分布:贝塔分布α=α_prior+n_success, β=β_prior+n_failure
alpha_post = alpha_prior + n_success
beta_post = beta_prior + n_failure
# 4. 绘制先验、似然、后验对比
x = np.linspace(0, 1, 1000)
# 先验PDF
prior_pdf = beta.pdf(x, alpha_prior, beta_prior)
# 后验PDF
post_pdf = beta.pdf(x, alpha_post, beta_post)
# 似然(伯努利分布的似然函数)
likelihood = x**n_success * (1-x)**n_failure
likelihood = likelihood / np.max(likelihood) # 归一化
# 绘图
fig, ax = plt.subplots(figsize=(10, 6))
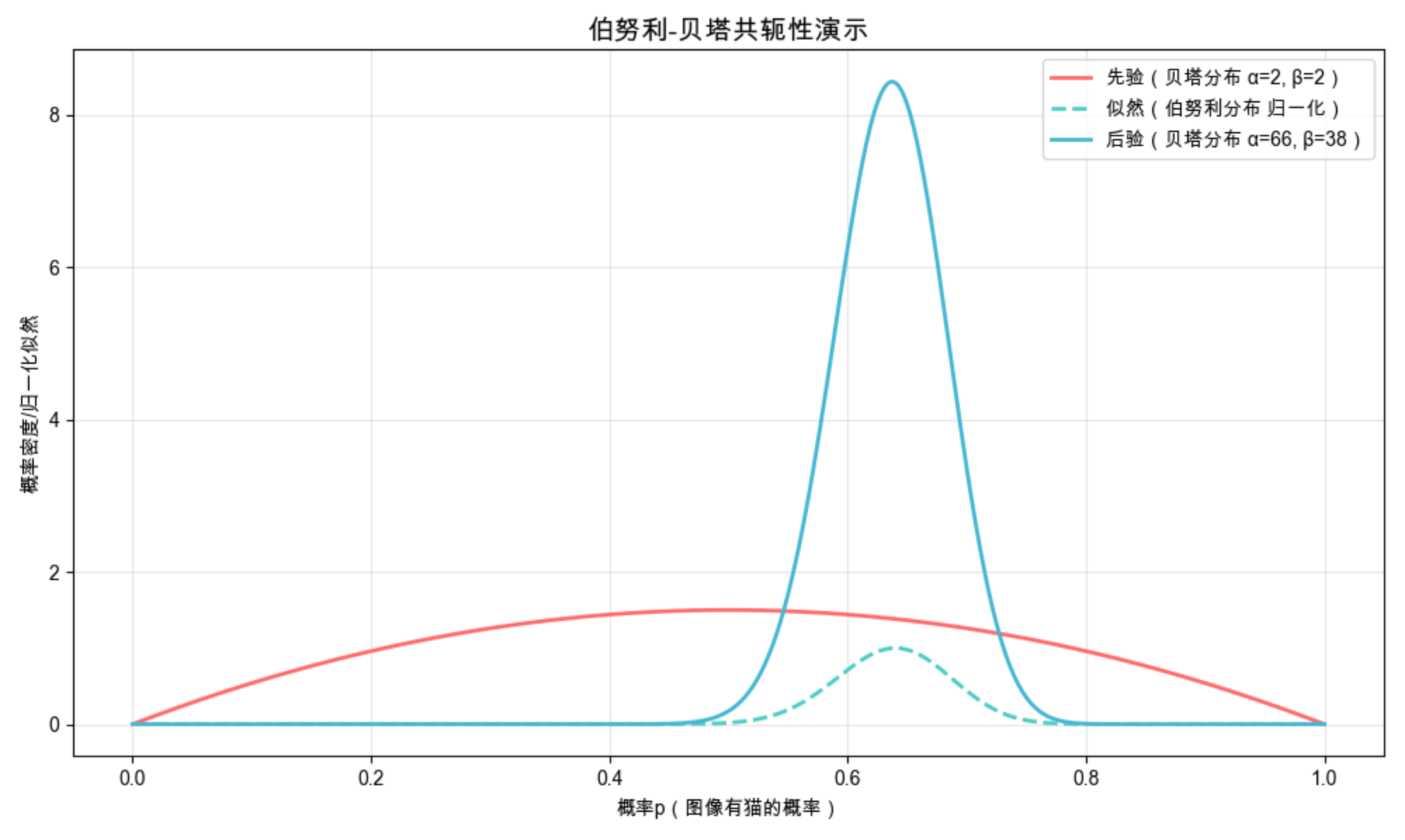
ax.plot(x, prior_pdf, label='先验(贝塔分布 α=2, β=2)', color='#FF6B6B', linewidth=2)
ax.plot(x, likelihood, label='似然(伯努利分布 归一化)', color='#4ECDC4', linewidth=2, linestyle='--')
ax.plot(x, post_pdf, label=f'后验(贝塔分布 α={alpha_post}, β={beta_post})', color='#45B7D1', linewidth=2)
ax.set_title('伯努利-贝塔共轭性演示', fontsize=14, fontweight='bold')
ax.set_xlabel('概率p(图像有猫的概率)')
ax.set_ylabel('概率密度/归一化似然')
ax.legend()
ax.grid(alpha=0.3)
plt.tight_layout()
plt.show()代码解释
共轭性的核心:后验分布的类型和先验一致,仅参数更新(α= 先验 α+ 成功次数,β= 先验 β+ 失败次数);
从图中能看到:后验分布结合了先验和似然的信息,比先验更贴近真实的 p=0.6;
这是计算机视觉中贝叶斯推断最常用的简化技巧。
应用场景
计算机视觉中用于快速贝叶斯推断 :比如在实时目标检测中,快速更新目标存在的概率,无需复杂计算。
总结
1.概率分布是计算机视觉的数学基础,不同分布对应不同场景:二分类用伯努利 / 贝塔,多分类用分类 / 狄利克雷,连续特征用正态 / 正态逆伽马(一元)、多元正态 / 正态逆维希特(多维);
2.共轭性是简化贝叶斯推断的核心技巧,核心共轭对需牢记(伯努利 - 贝塔、分类 - 狄利克雷、正态 - 正态逆伽马);
3.所有分布的核心是 "参数",参数决定分布形状,可视化能直观理解参数的影响。
备注
1.所有代码均适配 Mac 系统,Windows 用户只需将字体配置改为plt.rcParams['font.sans-serif'] = ['SimHei']即可;
2.代码中使用的scipy.stats是 Python 统计建模的标准库,安装命令:pip install scipy matplotlib numpy;
3.实际应用中,可根据数据特点调整分布参数,比如图像噪声的正态分布参数需根据噪声类型适配。
习题
1.修改伯努利分布代码,将试验次数改为 10000 次,观察实际概率是否更接近理论值;
2.调整多元正态分布的协方差矩阵,尝试生成 "更扁" 的椭圆形等高线,理解 σ 对分布形状的影响;
3.基于共轭性代码,尝试将先验改为 α=0.5, β=0.5(U 型贝塔分布),观察后验分布的变化;
4.思考:为什么计算机视觉中很多特征都假设服从正态分布?实际场景中哪些特征不服从正态分布?
最后
如果觉得这篇内容有帮助,欢迎点赞、收藏、关注!如果有代码运行问题或知识点疑问,评论区留言,我会及时回复~