文章目录
- [1. 什么是递归](#1. 什么是递归)
-
- [1.1 最简单的递归演示](#1.1 最简单的递归演示)
- [1.2 递归的思想](#1.2 递归的思想)
- [1.3 递归的限制条件](#1.3 递归的限制条件)
- [2. 递归举例](#2. 递归举例)
-
- [2.1 举例1:求n的阶乘](#2.1 举例1:求n的阶乘)
- [2.2 举例2:顺序打印一个整数的每一位](#2.2 举例2:顺序打印一个整数的每一位)
- [3. 递归与迭代](#3. 递归与迭代)
-
- [3.1 递归的优缺点](#3.1 递归的优缺点)
- [3.2 迭代的优势](#3.2 迭代的优势)
- [3.3 举例3:求第n个斐波那契数(递归vs迭代)](#3.3 举例3:求第n个斐波那契数(递归vs迭代))
- [3.4 递归的适用场景](#3.4 递归的适用场景)
- [4. 拓展学习](#4. 拓展学习)
1. 什么是递归
递归是C语言函数学习中的重要话题,本质是一种解决问题的方法,在C语言中表现为函数自己调用自己。
1.1 最简单的递归演示
以下代码演示了递归的基本形式,但未设置终止条件,会陷入死递归并导致栈溢出(Stack overflow):
c
#include <stdio.h>
int main()
{
printf("hehe\n");
main();// main函数中调用自身
return 0;
}运行结果 :

1.2 递归的思想
递归的核心思想是大事化小:将一个大型复杂问题层层拆分为与原问题相似但规模更小的子问题,直到子问题无法再拆分(递归终止),最后通过子问题的解逐步推导原问题的解。
"递"指递推 (拆分问题),"归"指回归(合并结果)。
1.3 递归的限制条件
书写递归代码必须满足两个必要条件,否则会导致死递归:
- 存在限制条件,当满足该条件时递归停止;
- 每次递归调用后,问题规模越来越接近限制条件。
2. 递归举例
2.1 举例1:求n的阶乘
正整数n的阶乘 n! 是所有小于等于n的正整数的乘积,0的阶乘为1,公式为:
n ! = n × ( n − 1 ) × ( n − 2 ) × . . . × 1 n! = n \times (n-1) \times (n-2) \times ... \times 1 n!=n×(n−1)×(n−2)×...×1
通过推导可将问题拆分:
n ! = n × ( n − 1 ) ! n! = n \times (n-1)! n!=n×(n−1)!
有⼀种有特殊情况是:当 n==0 的时候, n! 是1,其余 n! 都可以通过上面的公式计算。这样就能写出 n! 的递归公式如下:
F a c t ( n ) = { 1 ( n = = 0 ) n × F a c t ( n − 1 ) ( n > 0 ) Fact(n) = \begin{cases} 1 & (n==0) \\ n \times Fact(n-1) & (n>0) \end{cases} Fact(n)={1n×Fact(n−1)(n==0)(n>0)
完整代码:
c
#include <stdio.h>
int Fact(int n)
{
if(n == 0)
return 1; // 递归终止条件
else
return n * Fact(n-1); // 递推:调用自身解决更小问题
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fact(n);
printf("%d\n", ret);
return 0;
}运行结果(不考虑n太大溢出的情况):
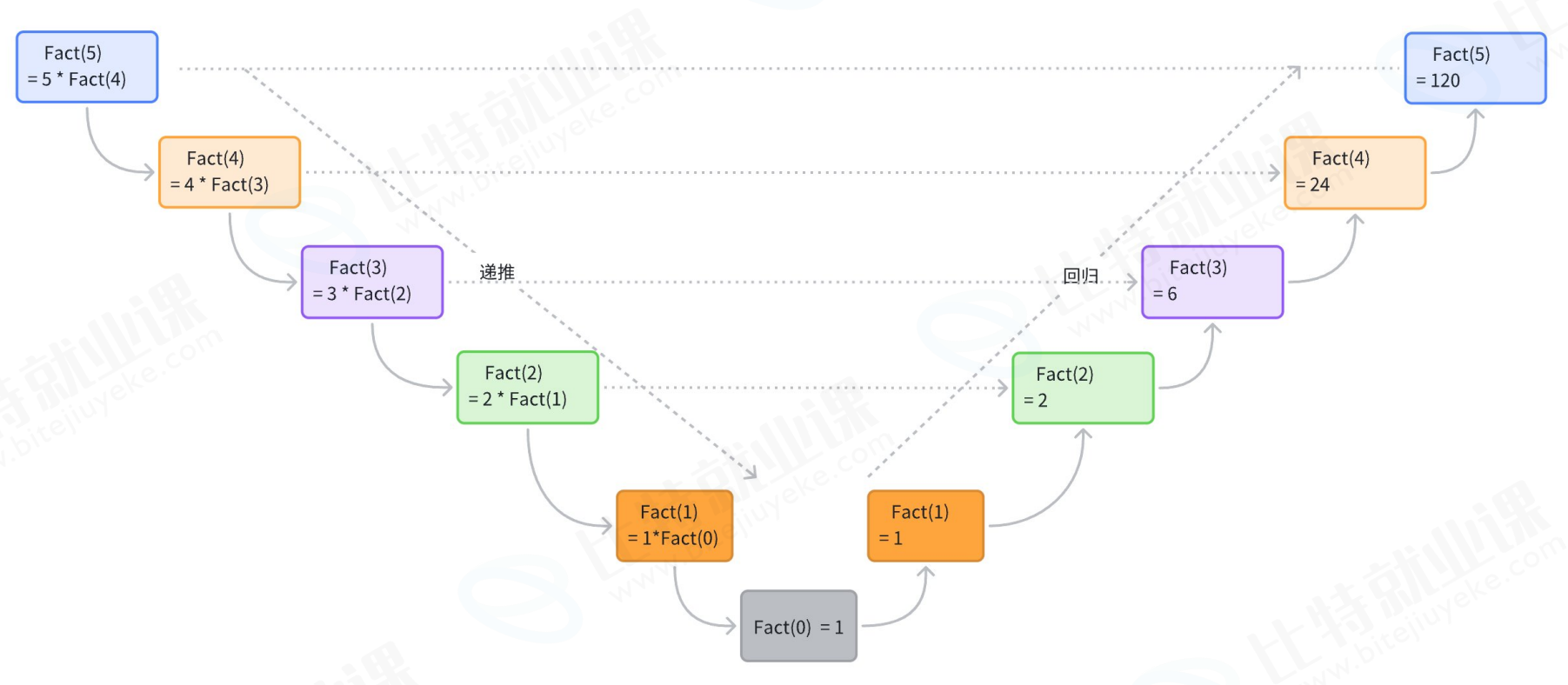
5
120画图推演 (以n=5为例):
2.2 举例2:顺序打印一个整数的每一位
输入一个整数m,按顺序打印其每一位(如输入1234,输出1 2 3 4;输入520,输出5 2 0)。
核心思路:
- 通过
n%10可获取最低位,但顺序颠倒; - 递归拆分:先打印n的前n-1位(
Print(n/10)),再打印最低位(n%10); - 限制条件:n为个位数时(n≤9),直接打印。
完整代码:
c
#include <stdio.h>
void Print(int n)
{
if(n > 9) // 递归条件:n不是个位数
{
Print(n/10); // 递推:打印前n-1位
}
printf("%d ", n%10); // 回归:打印当前最低位
}
int main()
{
int m = 0;
scanf("%d", &m);
Print(m);
return 0;
}运行结果:
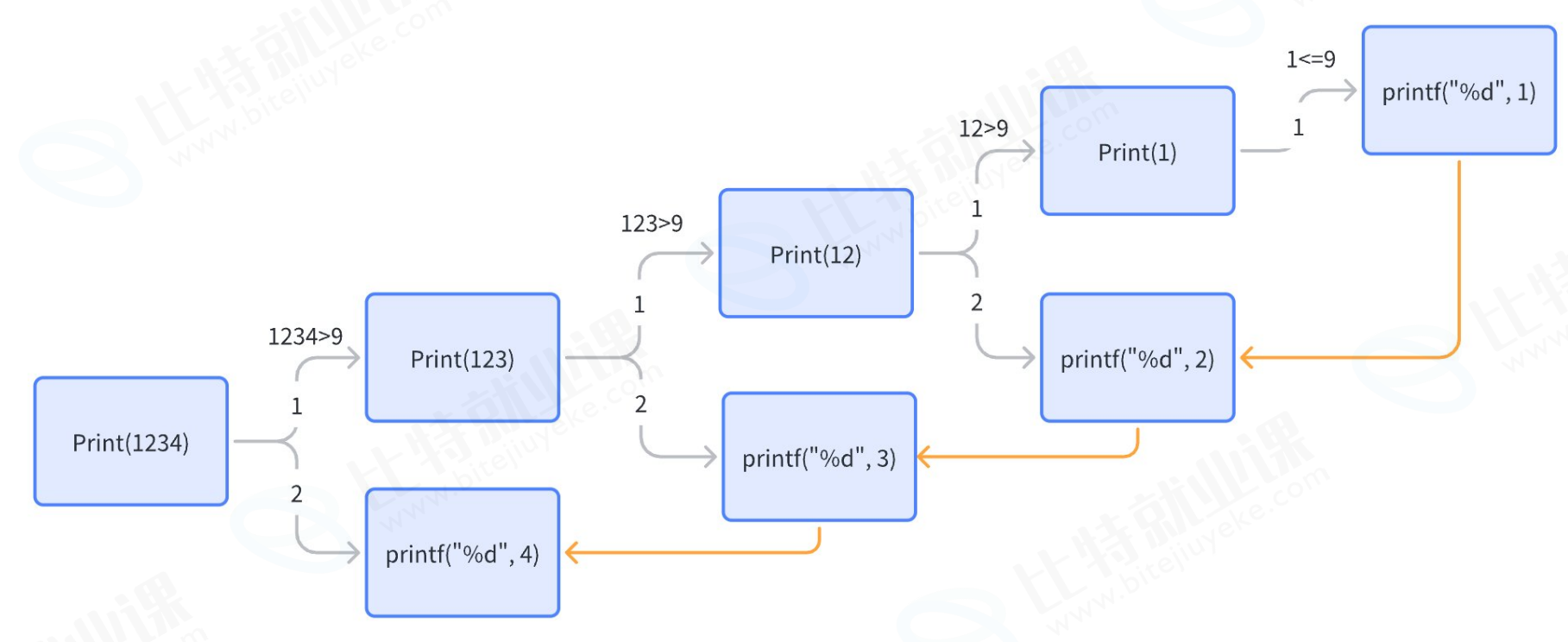
1234
1 2 3 4画图推演 (以n=1234为例):
3. 递归与迭代
3.1 递归的优缺点
优点
- 代码简洁,逻辑清晰,符合"大事化小"的思维习惯;
- 适合解决复杂问题(如树/图遍历、分治算法),迭代实现难度高。
缺点
- 每次递归调用需在栈区开辟函数栈帧(保存局部变量、返回地址等),存在运行时开销;
- 递归层次过深可能导致栈溢出(Stack overflow);
- 部分场景存在大量冗余计算,效率低下。
3.2 迭代的优势
迭代(通常指循环)无需函数调用开销,不存在栈溢出风险,多数场景下效率更高。对于可拆分的简单问题,优先考虑迭代实现。
3.3 举例3:求第n个斐波那契数(递归vs迭代)
斐波那契数定义:第1、2个数为1,从第3个数开始,每个数等于前两个数之和,公式为:
F i b ( n ) = { 1 ( n < = 2 ) F i b ( n − 1 ) + F i b ( n − 2 ) ( n > 2 ) Fib(n) = \begin{cases} 1 & (n <= 2) \\ Fib(n-1) + Fib(n-2) & (n > 2) \end{cases} Fib(n)={1Fib(n−1)+Fib(n−2)(n<=2)(n>2)
递归实现(不推荐):
c
#include <stdio.h>
int Fib(int n)
{
if(n <= 2)
return 1;
else
return Fib(n-1) + Fib(n-2);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
return 0;
}问题 :存在大量冗余计算。
例如当n输入为50的时候,需要很长时间才能算出结果,说明递归的写法是非常低效的。
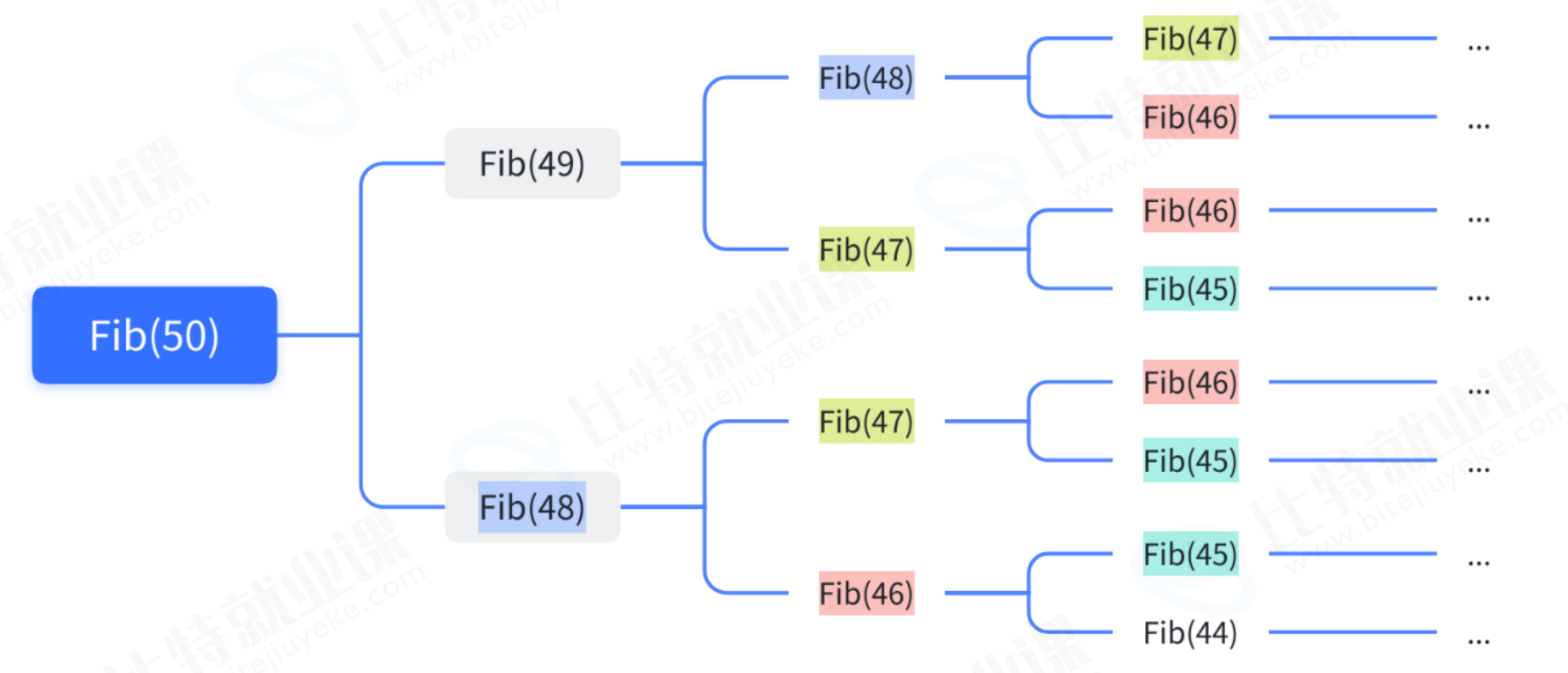
迭代实现 (推荐):
核心思路:从前往后计算,用变量保存前两个数,逐步推导第n个数。
c
#include <stdio.h>
int Fib(int n)
{
int a = 1; // 第1个斐波那契数
int b = 1; // 第2个斐波那契数
int c = 1; // 存储第n个斐波那契数(初始值适配n≤2)
while(n > 2) // 循环推导n>2的情况
{
c = a + b;
a = b; // 更新前两个数
b = c;
n--;
}
return c;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
return 0;
}优势:无冗余计算,时间复杂度O(n),效率远超递归。
3.4 递归的适用场景
递归并非万能,需根据场景选择:
- 优先使用迭代:问题简单、可循环推导(如阶乘、斐波那契数);
- 考虑使用递归:问题复杂、迭代实现难度高(如树遍历、汉诺塔、回溯算法)。
4. 拓展学习
以下问题适合用递归解决,可进一步练习:
- 青蛙跳台阶问题:一只青蛙一次可跳1级或2级台阶,求跳上n级台阶的总方式数;
- 汉诺塔问题:将n个盘子从A柱移动到C柱,中间可借助B柱,每次只能移动1个盘子且大盘不能压小盘。