文章目录
前言
接上一篇的算法内容,这篇来讲解"二分法"。
介绍
在 C++ 算法中,二分法是基于有序序列和双向指针(迭代器)实现的高效查找算法,核心逻辑仍是通过不断折半缩小查找范围,时间复杂度为O(log_2n)。C++ 对二分法的支持分为手动实现和标准库算法两种形式,其中标准库<algorithm>头文件提供了现成的二分查找函数,是实际开发中更常用的方式。
二分查找
1.题目解析
在看题目时,一定要看清题目的条件;
此题可以把 left,right 定义相反双指针,若用双指针方法来解答,时间复杂度不是最优解;
所以采用二分法的方法来解答此题
2.算法原理
二分法:简单来说,是把一段数组分为二段的一种方法;
其本质是,当数组有二段性时,无论数组是有序还是无序,能把数组变成两部分,根据规律选取两部分后,竟而在两部分中的另一个部分时可继续查找。
写代码时,需要注意的细节问题:
1.循环条件:left <= right ,防止因为循环越界;
2.找中点:left+(right-left)/2 或 left+(right-left+1)/2 ,当数组是偶数形式时用该公式(left+right+1)/2,可防溢出;
3.时间复杂度:
总结朴素二分查找模版while(left<=right)
{
//(right-left)/2或(right-left+1)/2-->当数组是偶数形式时 (left+right+1)/2==》防溢出的方式
int mid=left+(right-left)/2;
if(....) //....是条件
left=mid+1;
else if (....)
right=mid-1;
else
return ....; //这里的....是看题目要求返回什么值
}
注:求中点的位置,可以划成三分/四分....n分,只要把left+(right-left)/2中的'2'改成'3/4...n',就可以变成三分法/四分法..../n分法
3.编写代码
cpp
class Solution {
public:
int search(vector<int>& nums, int target) {
//1.划分好二分
//2.(left+right)/2 容易出问题,在数据量大的时候,会直接超出int范围值,要换一种写法
//3.left+(right-left+1)/2 这里的2可以改成3,就能划分3分
//right是在数组最后一位,left是在首尾,俩者相减除2再加1就可以得到中间位置的下标,再加left就可以知道划分的二分区域在哪
int left=0,right=nums.size()-1;
while(left<=right) //以防越界
{
//找到二分区域
int mid=left+(right-left+1)/2;
//如果mid的数小于目标数
if(nums[mid]<target)
left=mid+1;//如果小于,让left跑到mid+1的位置,变成[mid+1,target]
else if(nums[mid]>target)
right=mid-1;//如果大于,让right跑到mid-1的位置,变成[target,mid-1]
else return mid; //结果是要返回下标
}
return -1; //没有找到就返回-1
}
};在排序数组中查找元素的第一个和最后一个位置
1.题目解析
注:有减1,求中点就要+1
2.算法原理
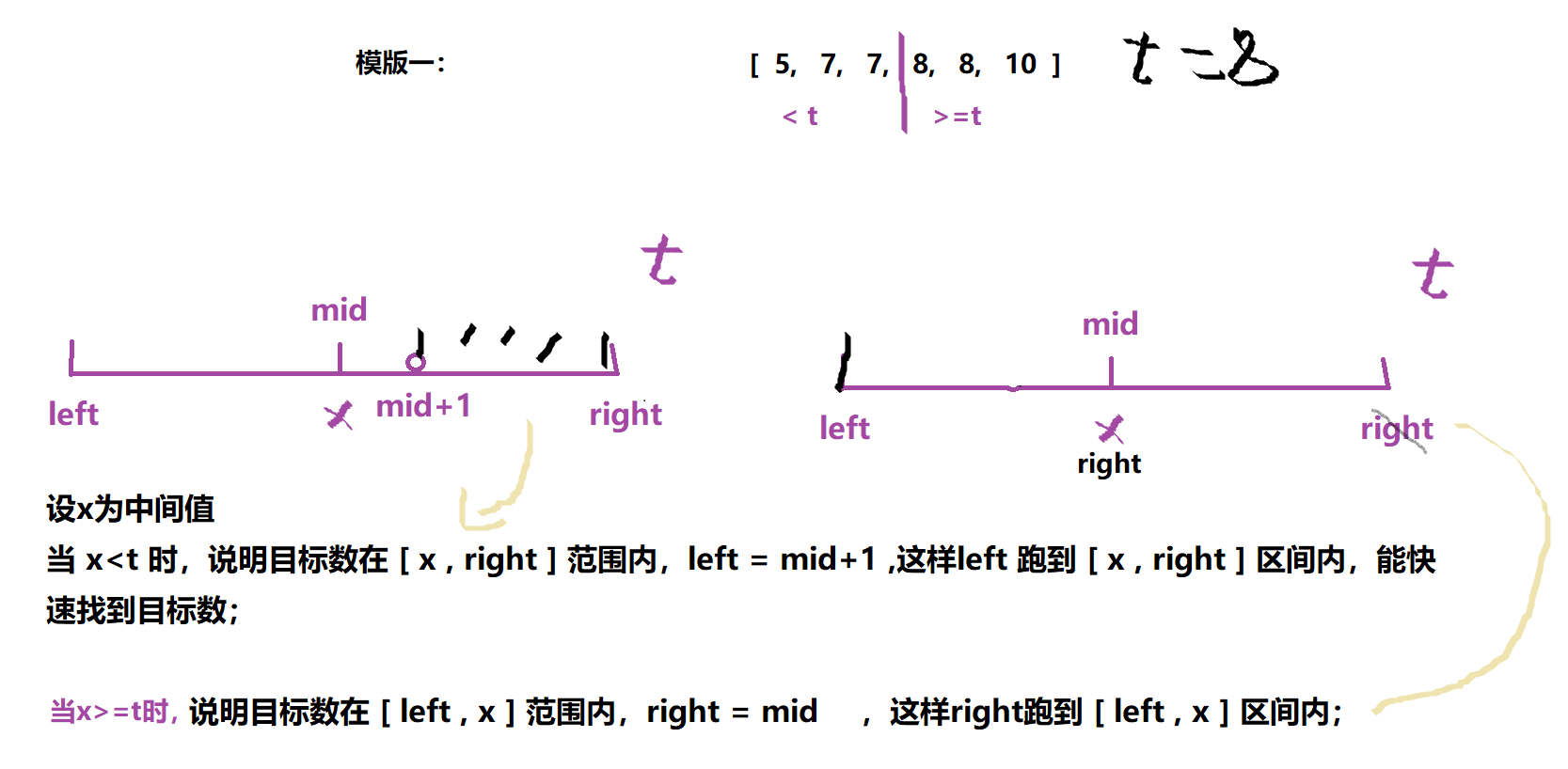
模版一:
细节问题:
1.循环条件,是left < right,如果是left<=right,就是最终结果无需判断,否则会死循环
2.求中间点,用left+(right-left)/2,如果用left+(right-left-1)/2求数量是偶数的数组,会出现死循环
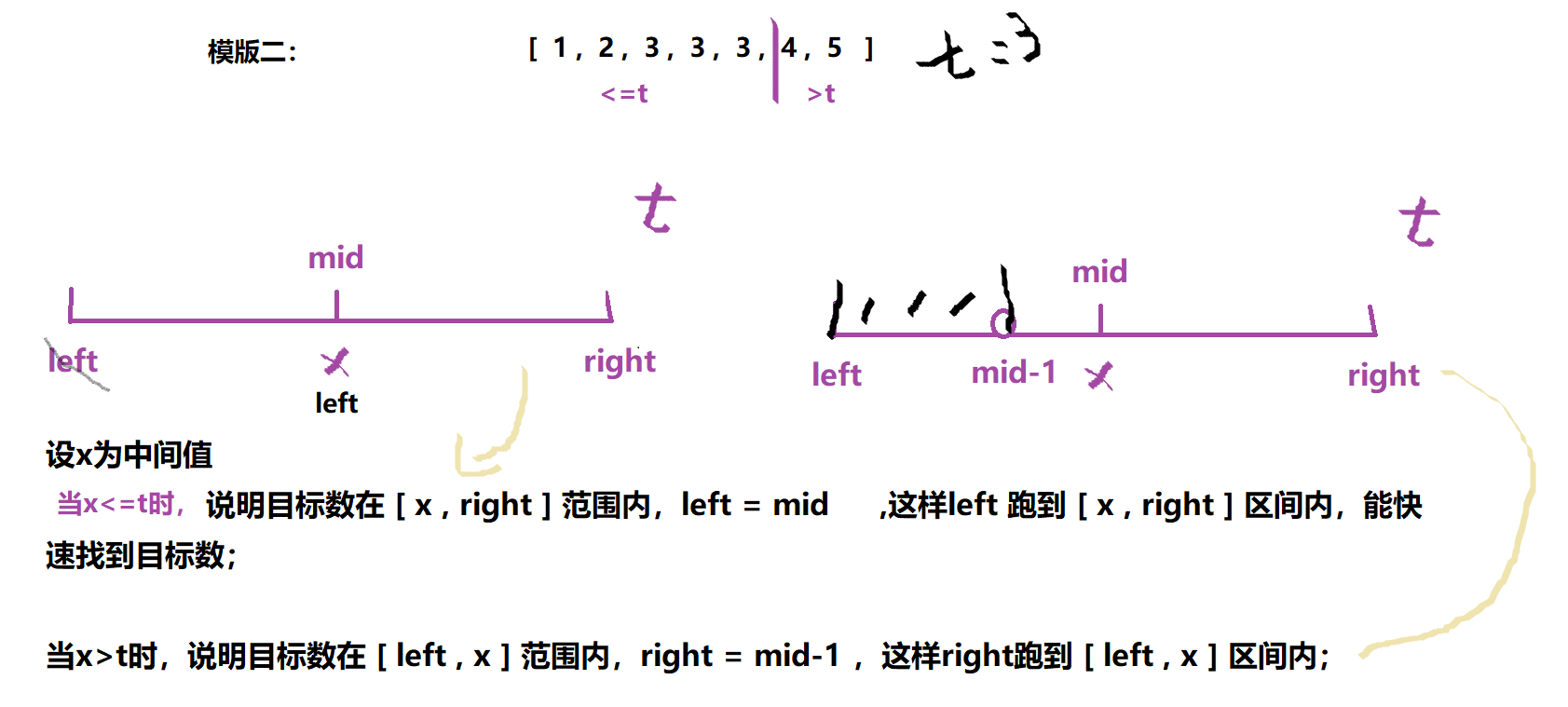
模版二:
细节问题:
1.循环条件,同上
2.求中间点,用left+(right-left+1)/2,如果用left+(right-left)/2求数量是奇数的数组,会出现死循环
总结模版
模版一:查找区间左端点的模版
while(left < right)
{
int mid=left+(right-left)/2;
if(....) //....是条件
left=mid+1;
else right=mid;
}
模版二:查找区间右端点的模版
while(left < right)
{
int mid=left+(right-left+1)/2;
if(....) //....是条件
left=mid
else right=mid-1;
}
注:判断条件是要根据题目要求来判断
3.编写代码
cpp
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
//1.防溢出,当数组为0,就返回[-1,-1]
if(nums.size()==0)
return {-1,-1};
int begin=0;
//2.二分左端点区间
int left=0,right=nums.size()-1;
//循环条件:left<right,不是<=,题目要求返回目标值的起始和结束位置,
//如果<=,就会导致ret(找到的目标数)=left=right,这样就会陷入循环,一直循环下去
while(left < right)
{
//找到中间点:用left+(right-left)/2,如果用left+(right-left-1)/2求数量是偶数的数组,会出现死循环
int mid=left+(right-left)/2;
if(nums[mid]<target)
left=mid+1;
else
right=mid;//right!=mid-1,是因为找到的目标数可能在mid的位置
}
//3.判断左端点区间是否有结果
if(nums[left]!=target)
{
return {-1,-1};
}
else begin=left;
//4.二分右端点区间
left=0,right=nums.size()-1;
while(left<right)
{
//找到中间点:用left+(right-left+1)/2,如果用left+(right-left)/2求数量是奇数的数组,会出现死循环
int mid=left+(right-left+1)/2;
if(nums[mid]<=target)
left=mid; //left!=mid+1,是因为找到的目标数可能在mid的位置
else right=mid-1;
}
return {begin,right};
}
};总结
非常感谢大家阅读完这篇博客。希望这篇文章能够为您带来一些有价值的信息和启示。如果您发现有问题或者有建议,欢迎在评论区留言,我们一起交流学习。