目录
- 一.概念
- 二.铺地毯
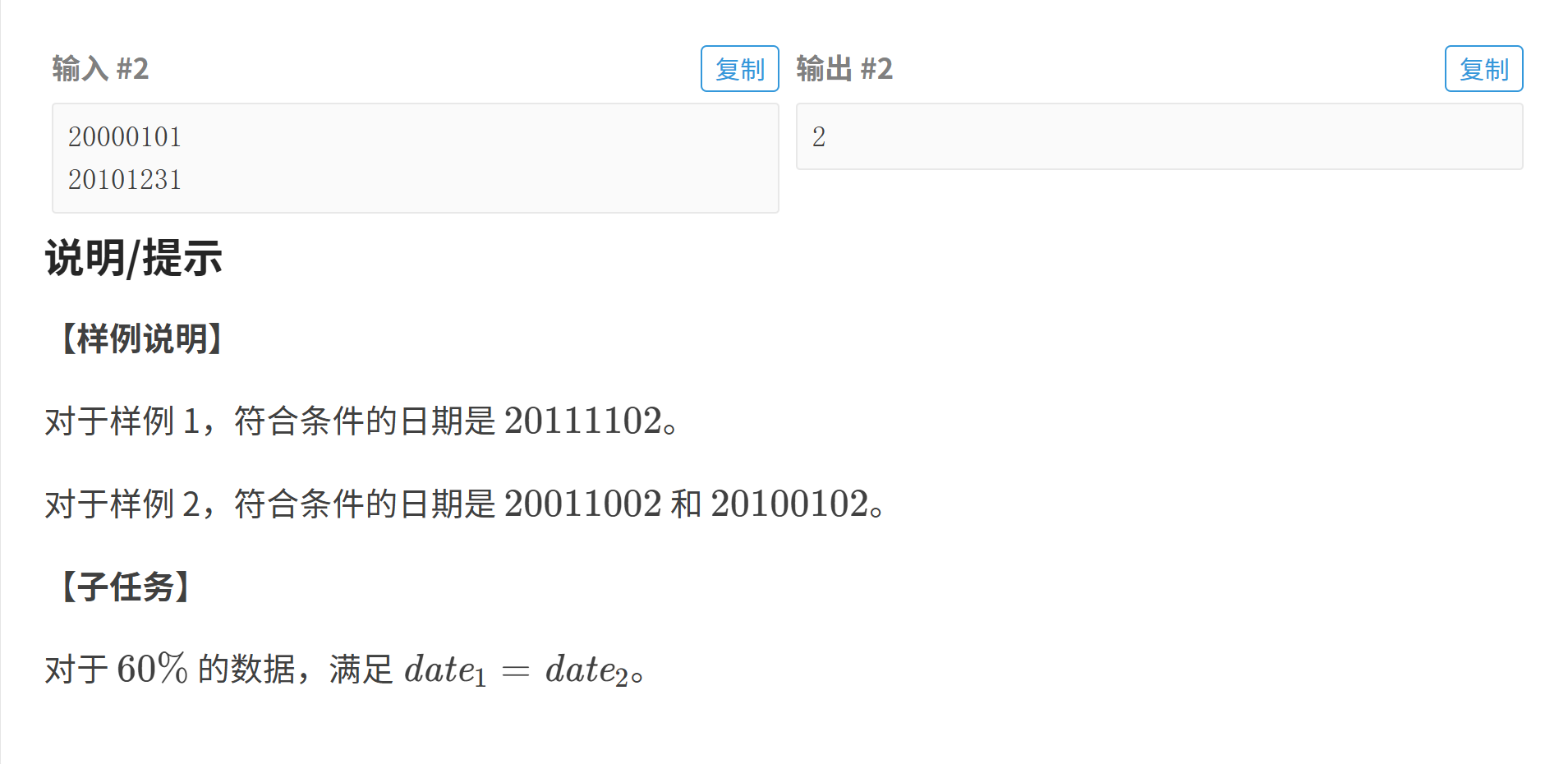
- 三.回文日期
- 四.扫雷
哈喽,编程搭子们!😜 又到了沉浸式敲代码的快乐时间~把生活调成「代码模式」,带着满满的热爱钻进编程的奇妙世界------今天也要敲出超酷的代码,冲鸭!🚀

✨ 我的博客主页:喜欢吃燃面
📚 我的专栏(持续更新ing):
《C语言》 |
《C语言之数据结构》 |
《C++》 |
《Linux学习笔记》
💖 超感谢你点开这篇博客!真心希望这些内容能帮到正在打怪升级的你~如果有任何想法、疑问,或者想交流学习心得,都欢迎留言/私信,咱们一起在编程路上互相陪伴、共同进步呀!
一.概念
枚举(暴力枚举)核心要点:
- 本质 :穷举所有可能,筛选符合条件的结果,是纯暴力算法。
- 风险 :时间复杂度高,极易超时,需先根据数据范围判断可行性;不适用时用二分、双指针、前缀和与差分等优化。
- 关键三问 :
- 枚举什么(对象)
- 按什么顺序(正序/逆序)
- 用什么方式(普通/递归/二进制)
二.铺地毯
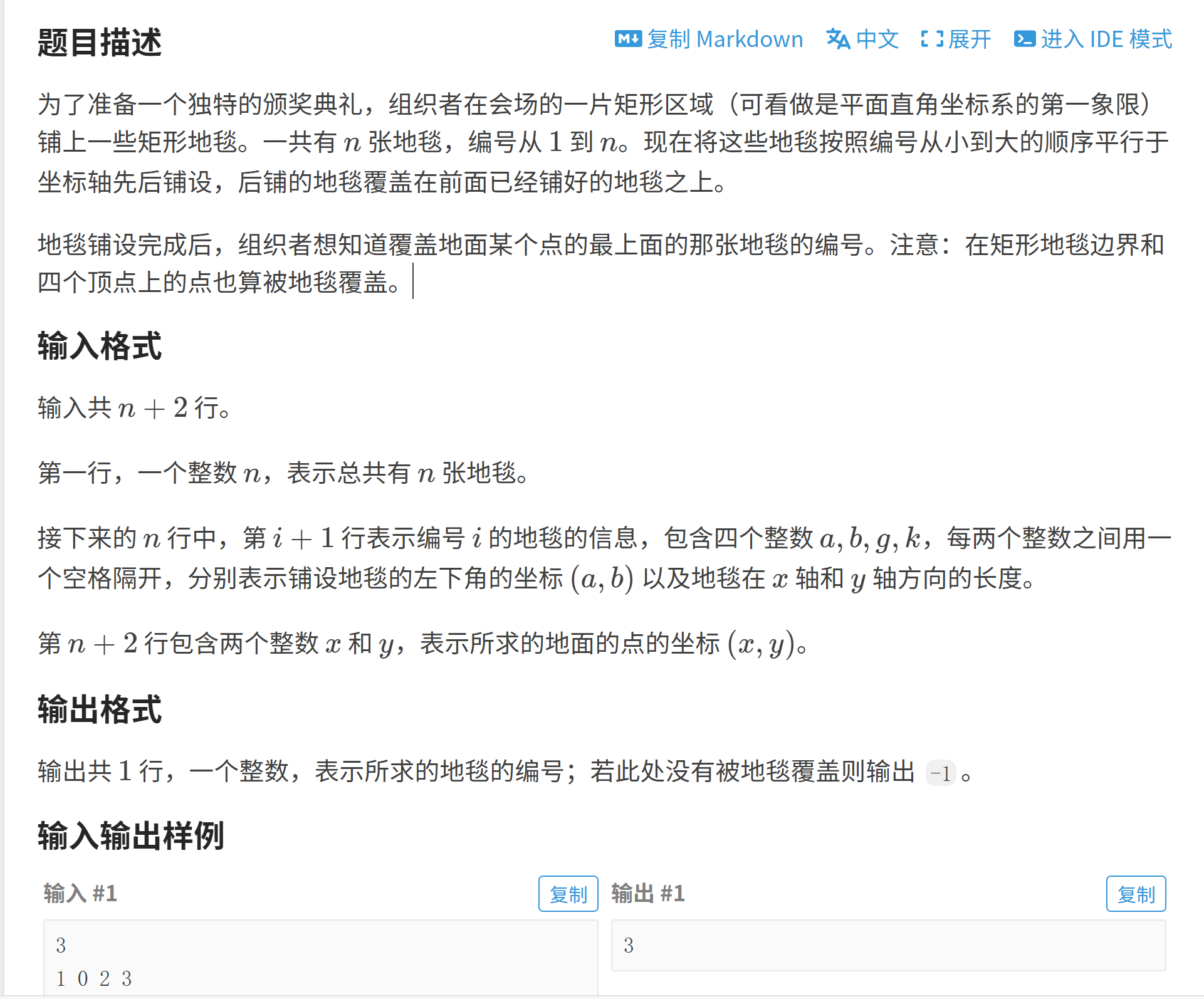
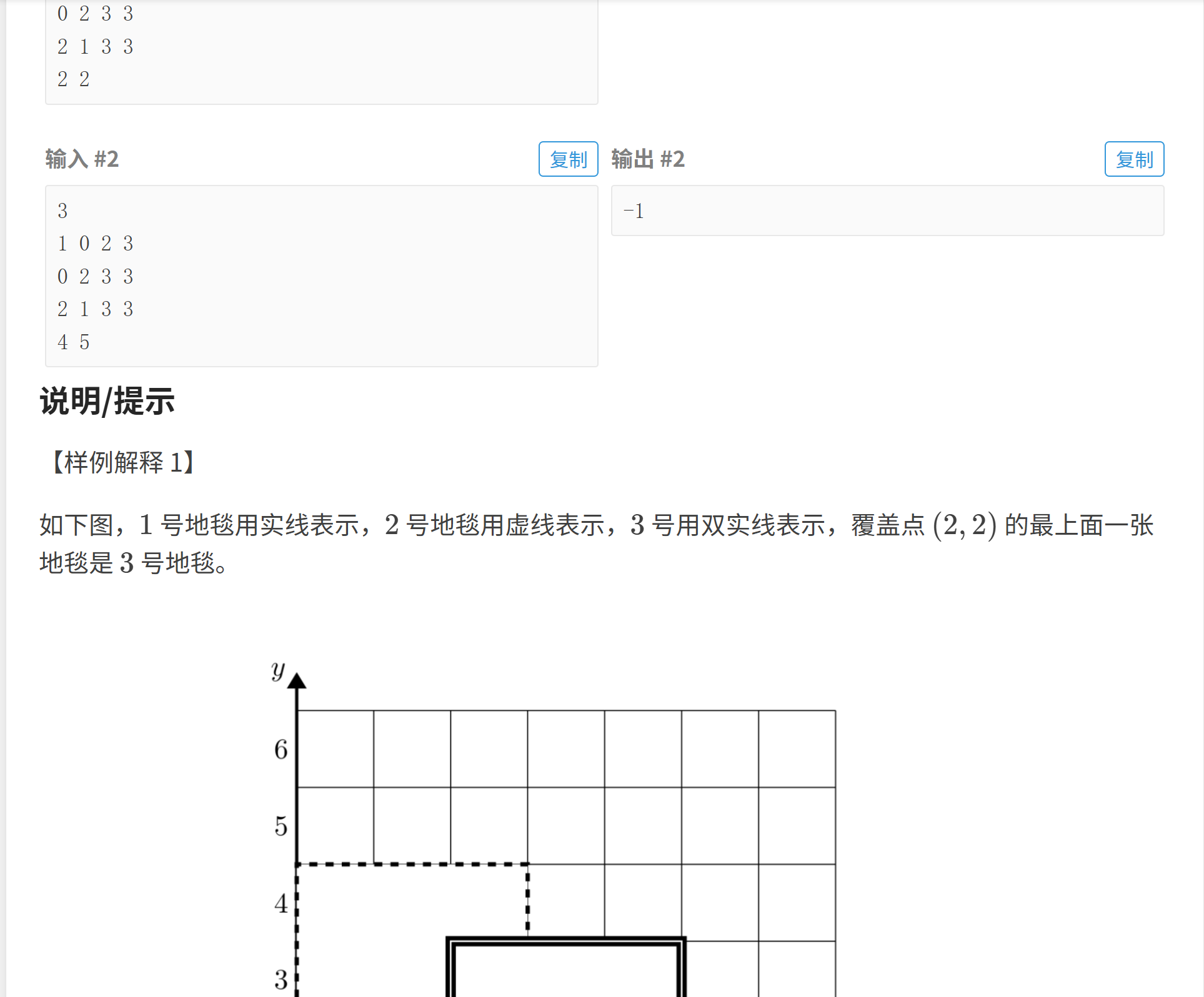
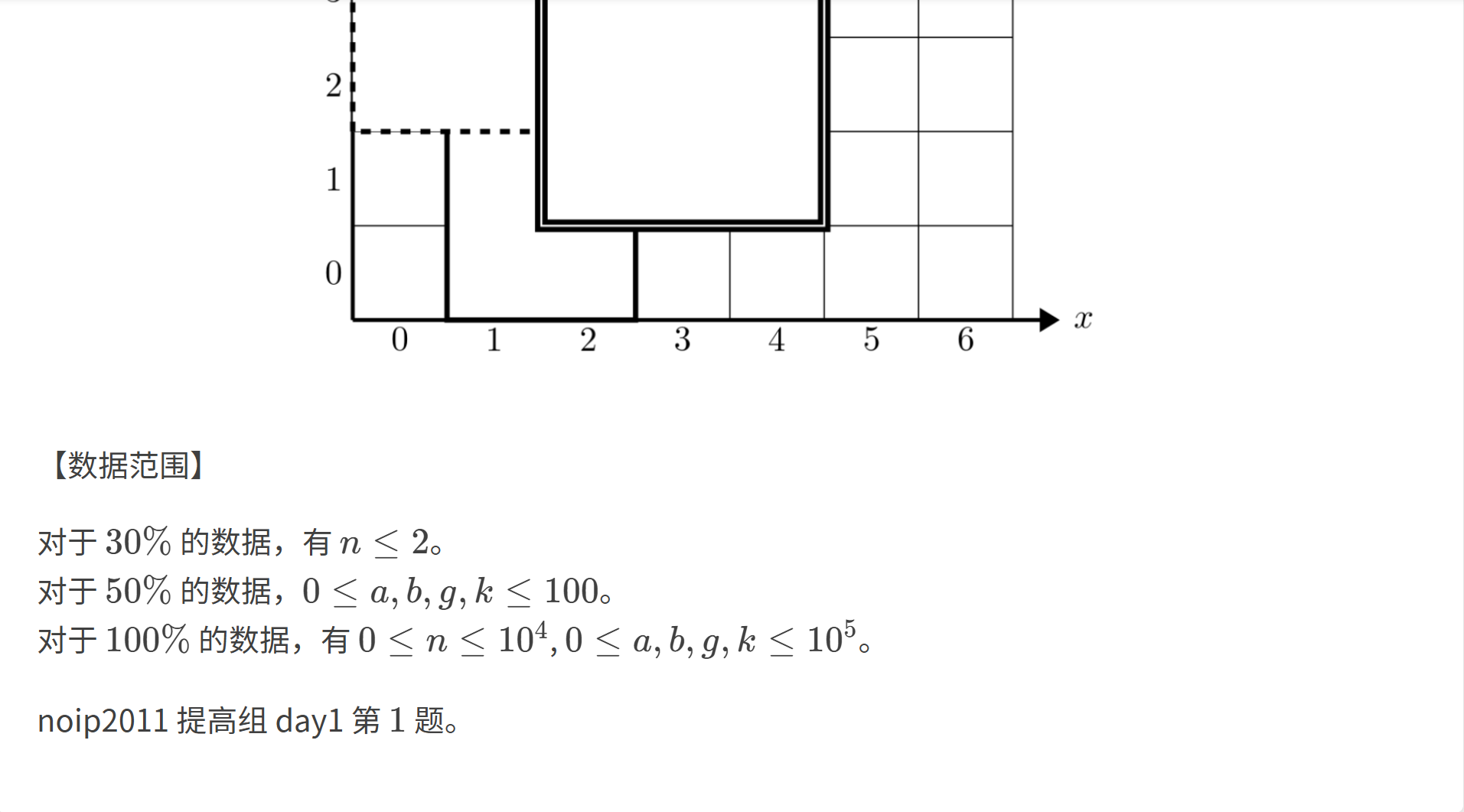
1.题目
2.解题思路
2.1 思路
- 输入处理 :读取地毯总数
n,再依次读取每张地毯的左下角坐标(a, b)及 x/y 轴方向长度g/k,将每张地毯的参数存储在数组中,按编号 1~n 对应。 - 查询判断 :读取目标点坐标
(x, y),从编号最大的地毯(最后铺设、最上层)开始倒序遍历,判断点是否在地毯覆盖范围内(x ∈ [a, a+g] 且 y ∈ [b, b+k])。 - 结果输出 :找到第一个覆盖目标点的地毯则输出其编号并终止程序;若遍历完所有地毯都未找到,输出
-1。
2.2 解题关键步骤
- 地毯覆盖范围
- 倒序遍历(优先最上层)
- 坐标范围判断
- 数组存储参数
- 边界包含判断
- 提前终止遍历
3.参考代码
cpp
#include<iostream>
#include<vector>
using namespace std;
// 定义数组最大容量:适配题目中可能的最大地毯数量(1e5 + 10)
const int N = 1e5 + 10;
// 全局数组:v[i] 存储第i张地毯的参数,每个vector包含4个int:
// a(左下角x)、b(左下角y)、g(x轴方向长度)、k(y轴方向长度)
vector<int> v[N];
// 标记变量:1表示找到覆盖目标点的地毯,0表示未找到(全局变量默认初始化为0)
int sign;
int main()
{
// 1. 输入地毯总数n
int n;
cin >> n;
// 2. 循环读取n张地毯的信息并存储
for (int i = 1; i <= n; i++)
{
// a: 地毯左下角x坐标
// b: 地毯左下角y坐标
// g: 地毯在x轴方向的长度(向右延伸的长度)
// k: 地毯在y轴方向的长度(向上延伸的长度)
int a, b, g, k;
cin >> a >> b >> g >> k;
// 将当前地毯的4个参数依次存入v[i]
v[i].push_back(a); // 第1个元素:左下角x坐标
v[i].push_back(b); // 第2个元素:左下角y坐标
v[i].push_back(g); // 第3个元素:x轴方向长度
v[i].push_back(k); // 第4个元素:y轴方向长度
}
// 3. 输入需要查询的地面点坐标(x, y)
int x, y;
cin >> x >> y;
// 4. 从编号最大的地毯开始倒序检查(后铺的地毯覆盖在上面,所以倒序找第一个覆盖点的就是最上面的)
for (int j = n; j >= 1; j--)
{
// 引用当前地毯的参数数组,避免重复拷贝,简化代码书写
vector<int>& carpet = v[j];
// 核心判断逻辑:点(x,y)是否被第j张地毯覆盖(包含边界和顶点)
// 地毯x范围:[a, a+g] 地毯y范围:[b, b+k]
if (x >= carpet[0] && x <= carpet[0] + carpet[2] && // x坐标在地毯水平范围内
y >= carpet[1] && y <= carpet[1] + carpet[3]) // y坐标在地毯垂直范围内
{
cout << j; // 找到最上面的地毯,输出其编号
sign = 1; // 标记为"找到"
return 0; // 直接退出程序,无需继续检查
}
}
// 5. 若该点未被任何地毯覆盖,输出-1
if (!sign) cout << -1;
return 0;
}三.回文日期
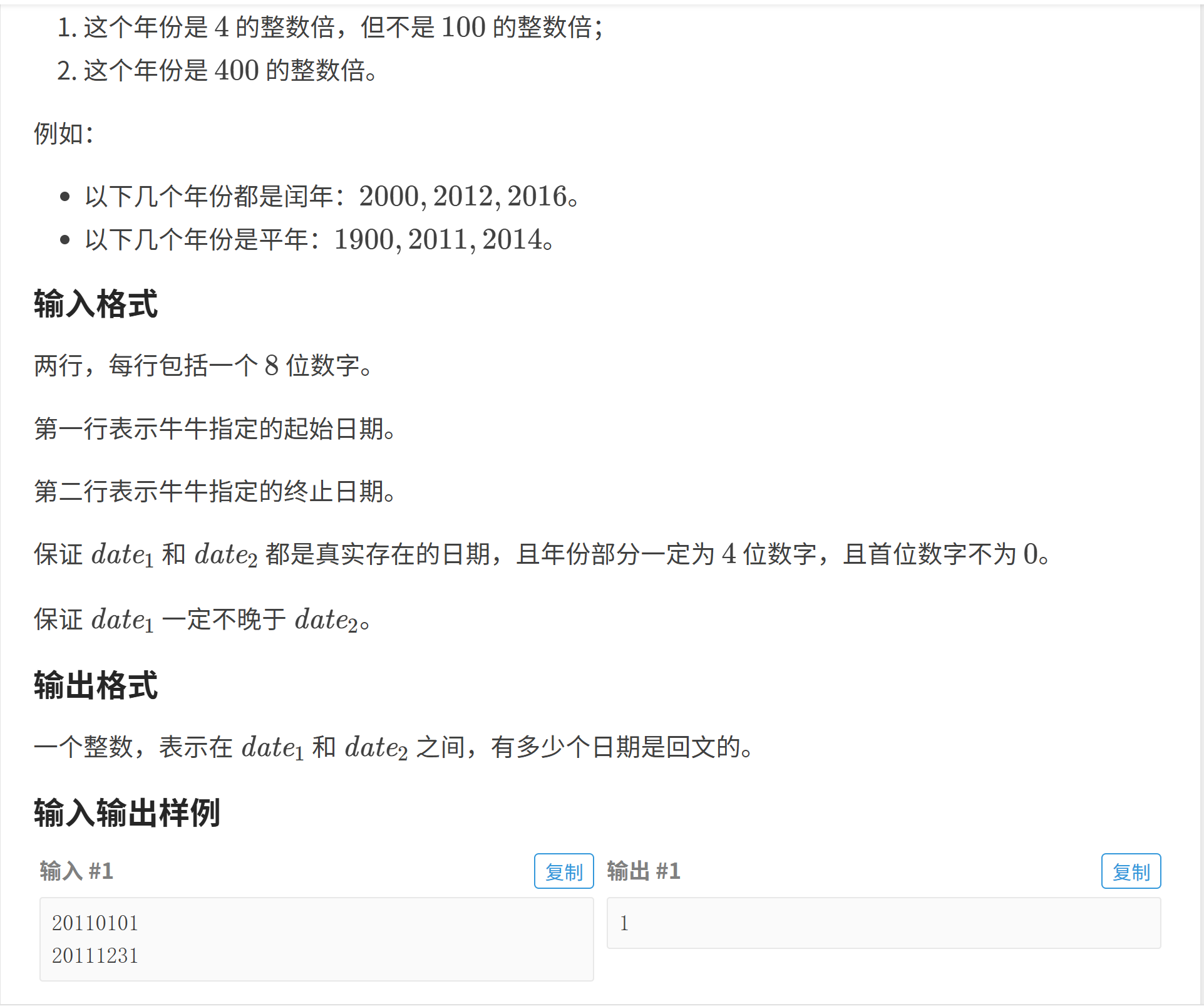
1.题目
2.解题思路
策略一:暴力枚举区间内所有数字
思路:从起始日期到结束日期,逐个遍历每一个数字,先判断它是否是回文数,如果是,再将其拆分为年、月、日,判断是否为合法日期。
- 优点:思路直观,容易实现。
- 缺点:时间复杂度高(区间跨度大时,如 20000101 ~ 20240101,有 2×10⁷ 次循环),容易超时。
核心步骤:
- 遍历区间内的每一个数字
d。 - 判断
d是否为回文数。 - 如果是回文数,将其拆分为年、月、日。
- 判断年、月、日是否合法(月份 1-12,日期 1-当月天数,闰年2月29天)。
- 如果合法,则计数加一。
策略二:枚举年份,生成回文月日
思路:只枚举区间内的年份,将年份的字符串反转,作为月和日的部分,再判断这个月日是否合法,从而生成完整的回文日期。
- 优点:时间复杂度大幅降低(如 2000 ~ 2024,仅 2×10³ 次循环),效率很高。
- 缺点:需要处理字符串反转和补零的细节。
核心步骤:
- 遍历区间内的每一个年份
y。 - 将
y转为字符串,反转后得到mmdd(月日)。 - 将
mmdd拆分为月m和日d。 - 判断
m和d是否合法(月份 1-12,日期 1-当月天数,闰年2月29天)。 - 如果合法,拼接出完整日期
y*10000 + m*100 + d,判断其是否在输入区间内,若是则计数加一。
策略三:枚举月日,拼接回文年份
思路:枚举所有可能的月和日组合(共 12×31 ≈ 372 种),将月日的字符串反转,作为年份的部分,拼接出完整的回文日期,再判断年份和日期是否合法。
- 优点:时间复杂度极低(仅约 372 次循环),是三种策略中效率最高的。
- 缺点:需要额外判断生成的年份是否在输入区间内。
核心步骤:
- 枚举所有月份
m(1-12)和日期d(1-当月天数)。 - 将
m和d格式化为两位字符串,拼接成mmdd。 - 反转
mmdd得到年份字符串yyyy。 - 判断
m和d是否合法(闰年2月29天)。 - 拼接出完整日期
yyyy + mmdd,判断其是否在输入区间内,若是则计数加一。
3.参考代码
法一:逐天遍历
cpp
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
int L, R; // 日期区间 [L, R](8位数字:年月日)
int mon[13] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 }; // 各月天数(索引0占位)
int ans = 0; // 回文日期计数
// 判断闰年(返回true为闰年)
bool leap(int y) {
return (y % 4 == 0 && y % 100 != 0) || (y % 400 == 0);
}
int main() {
cin >> L >> R;
// 拆分起始/结束日期为年/月/日
int y1 = L / 10000, m1 = L / 100 % 100, d1 = L % 100;
int y2 = R / 10000, m2 = R / 100 % 100, d2 = R % 100;
// 逐天遍历区间内所有日期
while (1) {
// 终止条件:当前日期超出结束日期
if (y1 > y2 || (y1 == y2 && m1 > m2) || (y1 == y2 && m1 == m2 && d1 > d2)) break;
// 校验当前日期是否为回文
string s = to_string(y1 * 10000 + m1 * 100 + d1);
string t = s;
reverse(t.begin(), t.end());
if (s == t) ans++;
// 日期+1(处理跨日/跨月/跨年)
d1++;
mon[2] = leap(y1) ? 29 : 28; // 动态更新2月天数
// 跨月处理
if (d1 > mon[m1]) {
d1 -= mon[m1];
m1++;
// 跨年处理
if (m1 == 13) {
m1 = 1;
y1++;
}
}
}
cout << ans << endl;
return 0;
}法二:高效遍历
cpp
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
int L, R; // 日期区间 [L, R](8位数字:年月日)
int mon[13] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 }; // 各月天数(索引0占位)
int ans = 0; // 回文日期计数
int year[100]; // 标记1-12月为合法月份(year[1~12]=1)
// 判断闰年(返回true为闰年)
bool leap(int y) {
return (y % 4 == 0 && y % 100 != 0) || (y % 400 == 0);
}
int main()
{
// 初始化:标记1-12月为合法月份
for (int i = 1; i <= 12; i++) year[i] = 1;
cin >> L >> R;
int y1 = L / 10000, y2 = R / 10000; // 提取区间起止年份
// 枚举区间内每一年,生成回文月日并校验
for (int i = y1; i <= y2; i++)
{
mon[2] = leap(i) ? 29 : 28; // 更新当年2月天数
string s = to_string(i); // 年份转字符串(如2020→"2020")
reverse(s.begin(), s.end()); // 年份逆序作为月日(2020→"0202")
int b = stoi(s); // 逆序字符串转数字("0202"→202)
int month = b / 100; // 提取月份(202/100=2)
int day = b % 100; // 提取日期(202%100=2)
// 校验:月份合法 + 日期合法 + 日期在区间内
int palindrome_date = i * 10000 + b; // 拼接完整回文日期
if (year[month] && day >= 1 && day <= mon[month] && palindrome_date >= L && palindrome_date <= R) {
ans++;
}
}
cout << ans;
return 0;
}法三:最优效率
cpp
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
string L, R; // 日期区间 [L, R](8位字符串:年月日)
int mon[13] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 }; // 各月天数(索引0占位)
int ans = 0; // 回文日期计数
// 数字转两位字符串(如1→"01",保证格式合法)
string two_digit(int x) {
if (x < 10) return "0" + to_string(x);
else return to_string(x);
}
// 判断闰年(返回true为闰年)
bool leap(int y) {
return (y % 4 == 0 && y % 100 != 0) || (y % 400 == 0);
}
int main()
{
cin >> L >> R;
// 枚举所有月份(1-12)
for (int m = 1; m <= 12; m++)
{
// 枚举当月所有日期(1-当月天数)
for (int d = 1; d <= mon[m]; d++)
{
if (d % 10 == 0) continue; // 跳过日期个位为0的情况(避免年份开头为0)
// 拼接月日为两位+两位字符串(如2月2日→"0202")
string mmdd = two_digit(m) + two_digit(d);
// 逆序月日得到年份("0202"→"2020")
string yyyy = mmdd;
reverse(yyyy.begin(), yyyy.end());
// 动态调整2月天数(闰年29天,平年28天)
int year = stoi(yyyy);
mon[2] = (m == 2 && leap(year)) ? 29 : 28;
// 校验日期合法性:仅当月日期≤当月天数时统计
if (d > mon[m]) continue;
// 拼接完整8位回文日期(年份+月日)
string date = yyyy + mmdd;
// 校验日期在区间内
if (date >= L && date <= R) ans++;
}
}
cout << ans;
return 0;
}总结
- 法一注释突出"逐天遍历"的暴力思路,明确终止条件和日期自增逻辑;
- 法二注释突出"枚举年份+生成回文月日"的高效思路,补充区间校验的关键注释;
- 法三注释突出"枚举月日+拼接回文年份"的最优思路,修正闰年判断的逻辑注释;
- 所有注释均简洁精准,不改变代码核心逻辑,仅提升可读性。
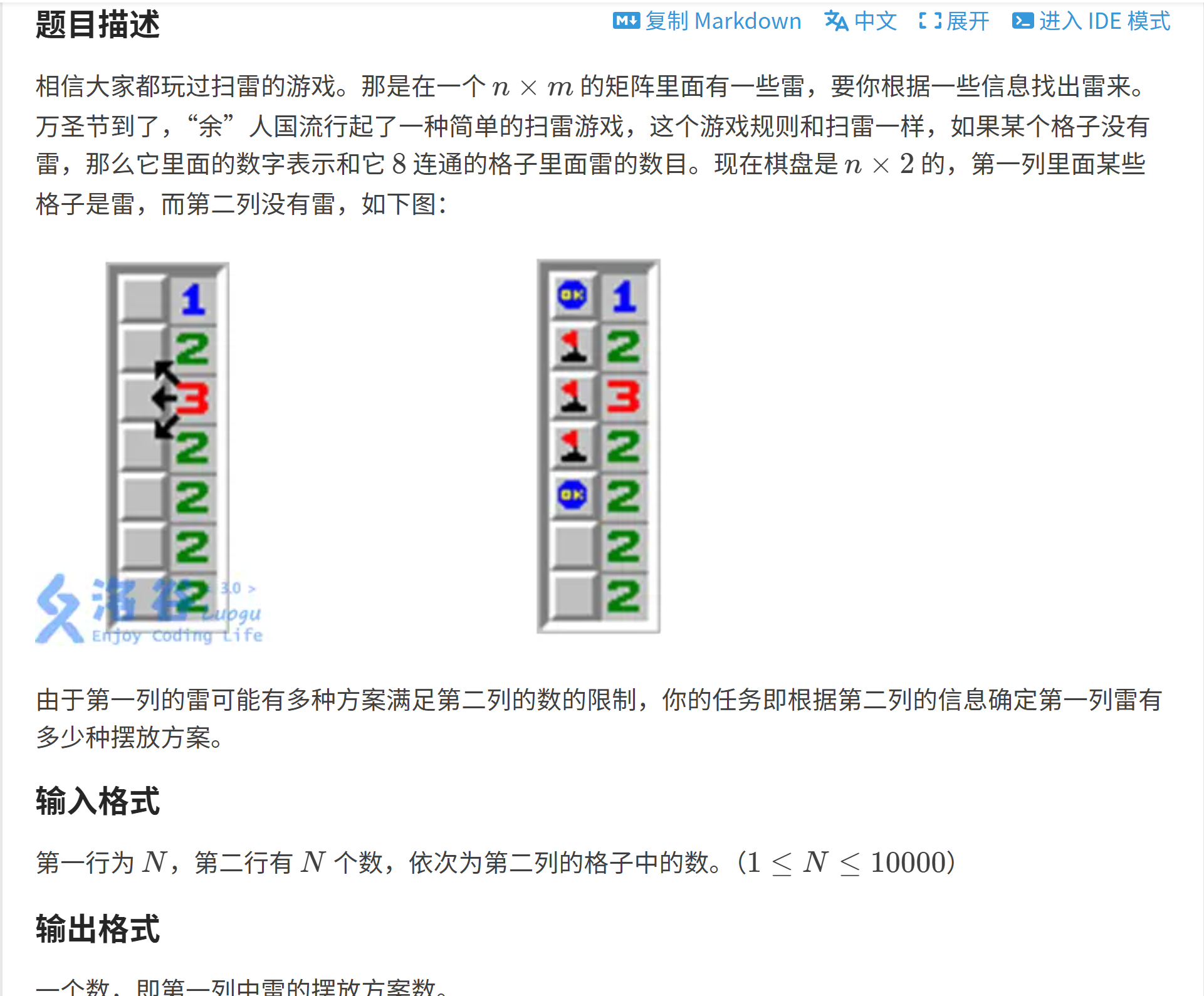
四.扫雷
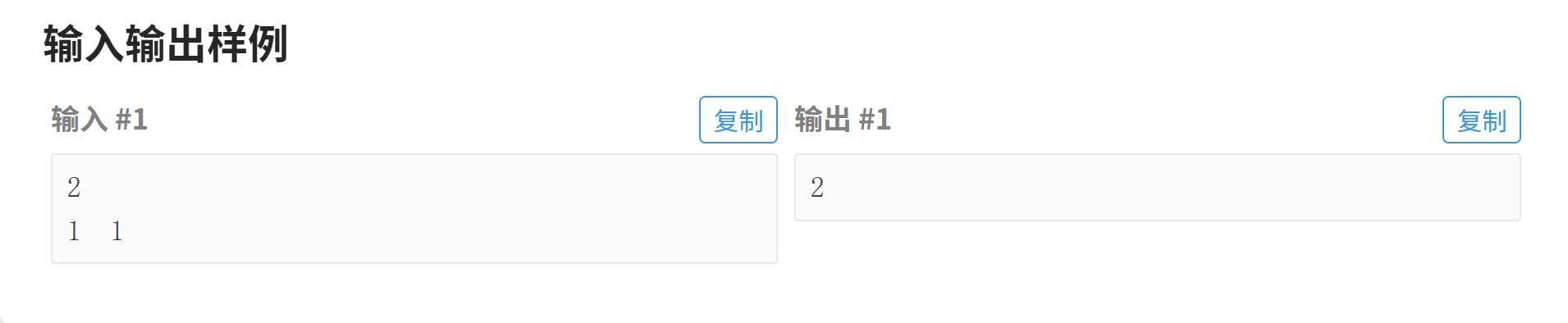
1.题目
2.解题思路
2.1 先明确题目规则(扫雷核心逻辑)
题目里的扫雷布局是两列格子:
- 第一列是待确定的地雷位置(用数组
a表示,a[i]=1有雷,a[i]=0无雷); - 第二列是已知的数字(用数组
b表示,b[i]代表第二列第i个格子显示的数字,等于它周围3个第一列格子的地雷总数)。
具体对应关系:
b[i] = a[i-1] + a[i] + a[i+1](a[0] 和 a[n+1] 是虚拟格子,默认无雷,值为0)。
2.2 核心解题思路:枚举 + 递推验证
这道题的关键是第一列的地雷分布由第一个格子唯一确定,因此只需枚举两种可能,再递推验证合法性:
步骤1:枚举第一个格子的状态(仅2种可能)
第一列第一个格子 a[1] 只有两种情况:
- 无雷:
a[1] = 0(对应代码中check1()函数); - 有雷:
a[1] = 1(对应代码中check2()函数)。
步骤2:递推计算后续所有格子的状态
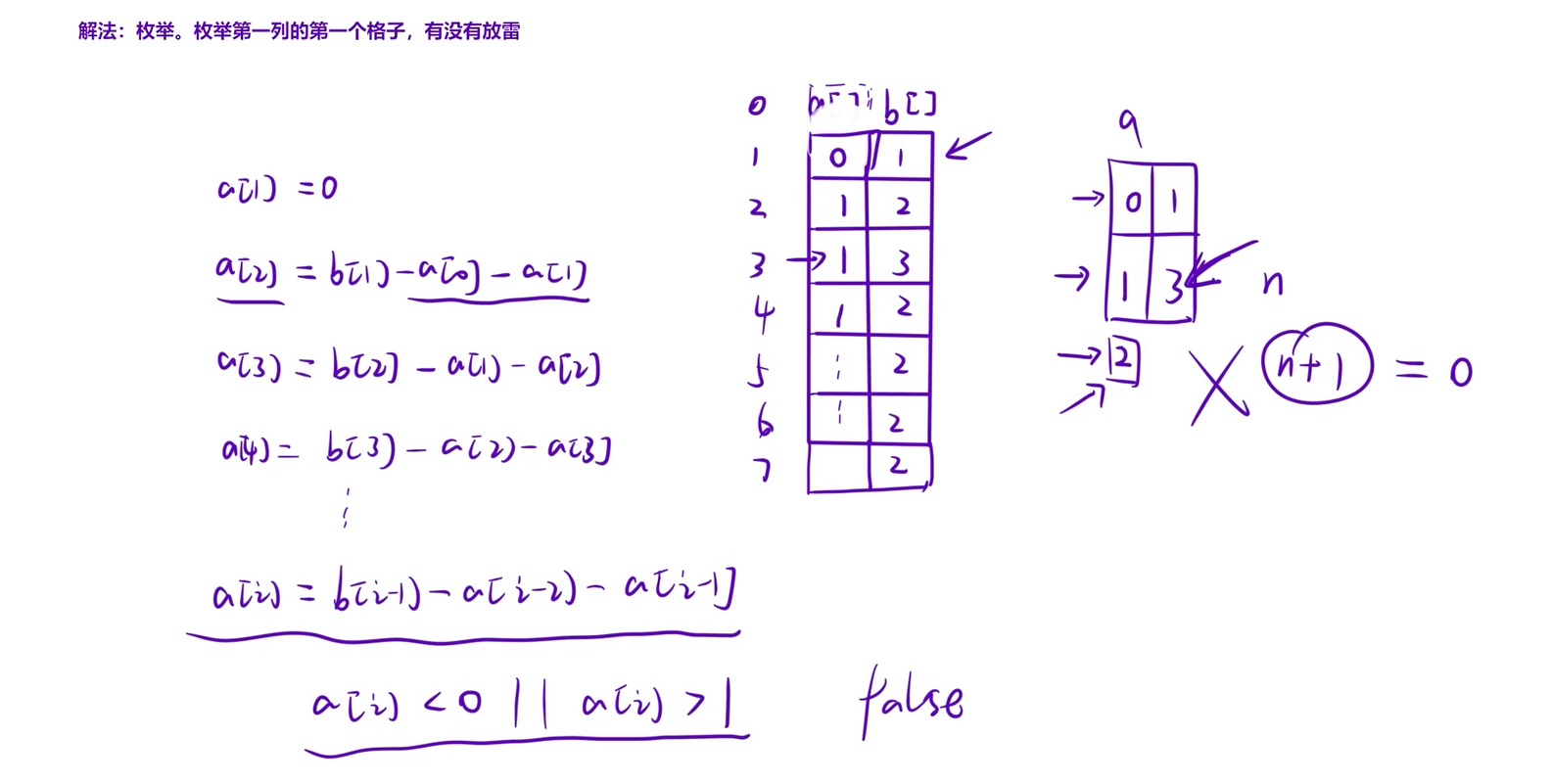
根据扫雷规则变形出递推公式:
从 b[i-1] = a[i-2] + a[i-1] + a[i] 可推导出:
a[i] = b[i-1] - a[i-1] - a[i-2]
代码中从 i=2 遍历到 i=n+1,就是用这个公式依次计算 a[2], a[3], ..., a[n+1]:
- 比如计算
a[2]:a[2] = b[1] - a[1] - a[0](a[0]=0,因为是虚拟格子); - 计算
a[3]:a[3] = b[2] - a[2] - a[1]; - 以此类推,直到计算出
a[n+1]。
步骤3:验证递推结果的合法性
递推过程中需要做两个检查:
- 中途合法性 :计算出的
a[i]必须是 0 或 1(地雷数只能是有/无,对应代码if(a[i]<0||a[i]>1)return 0); - 最终合法性 :递推到
a[n+1]时,必须等于 0(因为a[n+1]是虚拟格子,无雷,对应代码if(a[n+1]==0)return 1)。
步骤4:统计合法方案数
分别验证 a[1]=0 和 a[1]=1 两种情况,将合法的情况数相加(代码中 ret += check1() + check2()),最终输出总数。
2.3 代码逻辑与思路的对应关系
| 代码部分 | 对应解题思路 |
|---|---|
check1()/check2() |
枚举 a[1] 的两种初始状态 |
a[i] = b[i-1] - a[i-1] - a[i-2] |
核心递推公式 |
a[i]<0或a[i]>1 |
验证中途地雷数的合法性 |
a[n+1]==0 |
验证最后虚拟格子的合法性 |
ret += check1()+check2() |
统计所有合法方案数 |
总结
- 这道题的核心是利用"第一个格子决定所有格子"的特性,将无限可能的地雷分布简化为仅2种枚举情况;
- 递推公式是从扫雷规则变形而来,是连接已知(
b数组)和未知(a数组)的关键; - 验证环节需同时检查"中途值合法"和"最终虚拟格子合法",确保方案符合题目要求。
- 这个思路的时间复杂度是 O(n),对于题目中
n≤10000的数据范围,效率完全足够,也是这道题最简洁的解法。
3.参考代码
cpp
#include<iostream>
using namespace std;
int n; // 第二列数字的个数
const int N=1e4+10; // 数据范围,适配题目n≤1e4的限制
int a[N],b[N]; // a[]:第一列地雷分布(0无1有),b[]:第二列已知数字
// 检查a[1]=0(第一个位置无雷)时的方案是否合法
int check1()
{
a[1]=0;
// 递推计算a[2]到a[n+1],a[n+1]是虚拟格子(无雷)
for(int i=2;i<=n+1;i++)
{
a[i]=b[i-1]-a[i-1]-a[i-2]; // 扫雷规则推导的递推公式
if(a[i]<0||a[i]>1)return 0;// 地雷数只能是0/1,非法则返回0
}
return a[n+1]==0 ? 1 : 0; // 虚拟格子必须无雷,合法返回1
}
// 检查a[1]=1(第一个位置有雷)时的方案是否合法
int check2()
{
a[1]=1;
// 递推计算a[2]到a[n+1]
for(int i=2;i<=n+1;i++)
{
a[i]=b[i-1]-a[i-1]-a[i-2];
if(a[i]<0||a[i]>1)return 0;
}
return a[n+1]==0 ? 1 : 0;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)cin>>b[i]; // 输入第二列的已知数字
int ret=0;
ret+=check1();// 统计a[1]无雷的合法方案数
ret+=check2();// 统计a[1]有雷的合法方案数
cout<<ret; // 输出总合法方案数
return 0;
}