当RAG的“压缩包“爆了：如何检测Token溢出？

当RAG的"压缩包"爆了：如何检测Token溢出？

论文标题：Detecting Overflow in Compressed Token Representations for Retrieval-Augmented Generation

作者：Julia Belikova, Danila Rozhevskii, Dennis Svirin, Konstantin Polev, Alexander Panchenko

机构：Skoltech, Sber AI Lab, AIRI

会议：EACL 2026 Student Research Workshop

论文链接：https://arxiv.org/abs/2602.12235

🎯 一句话总结

RAG系统中的软压缩（如xRAG）把整篇文档塞进一个token，但信息装不下时就会"溢出"------这篇论文给出了检测溢出的方法：一个轻量级探测分类器，不需要跑LLM推理，只用投影后的表示就能达到0.72 AUC，相当于给压缩模块装了个"压力表"。

📖 这篇论文到底想解决什么问题？

想象你有一个行李箱（压缩token），要把一间房子的东西（长文档）塞进去。压缩技术能帮你折叠、真空打包，但总有个极限------箱子装不下的时候，东西就会从缝隙里掉出来。在RAG系统中，这个"东西掉出来"的现象就是Token溢出（Token Overflow）。

具体来说，问题出在**软压缩（Soft Compression）**这条技术路线上。当前的LLM在处理长上下文时面临巨大的计算开销，RAG系统检索到的文档动辄几百个token，拼接多个文档后上下文轻松破万。软压缩的思路是：与其让LLM逐字阅读，不如把文档"蒸馏"成几个密集的向量表示------也就是压缩token。

这里面最激进的代表是xRAG （NeurIPS 2024），直接把一整篇文档压缩成一个token。没错，175个token的文档，压成1个。压缩率175倍。

但问题来了：你怎么知道这一个token还能不能代表原文的关键信息？

如果用户问"文章里提到的实验数据是多少？"，而这个信息在压缩过程中被丢掉了，模型就只能瞎猜------更麻烦的是，模型不会告诉你它在瞎猜。这种"静默失败"才是最危险的。

这篇论文干的事情就是：给压缩模块加一个溢出检测器，在LLM开始生成答案之前就判断"这个压缩token还够用吗？"如果不够用，可以选择回退到完整文档，避免生成垃圾答案。

🧠 技术背景：xRAG是怎么把文档塞进一个Token的？

在深入溢出检测之前，有必要搞清楚被检测的对象------xRAG------到底是怎么工作的。

RAG的上下文困境

标准RAG的流程很直白：用户提问 → 检索相关文档 → 把文档文本拼在问题前面 → 送给LLM生成答案。问题在于，检索回来5篇文档，每篇200个token，加上问题本身，输入长度就到了1000+。这不仅慢，而且当文档数量增多时，KV Cache的显存开销也线性增长。

软压缩：把文本变成向量

软压缩的核心idea是：既然检索器已经把文档编码成了一个稠密嵌入向量（dense embedding），为什么不直接把这个向量喂给LLM，而非要解码回文本再编码一遍？

这有点像：你已经拍了一张照片（向量表示），为什么还要先把照片打印出来（解码成文本），再让另一个人重新拍一遍（LLM重新编码）？直接把照片传过去不好吗？

xRAG就是这么干的。它把检索器产生的文档嵌入向量 EEE 通过一个两层MLP投影器 W\mathbf{W}W 映射到LLM的词嵌入空间：

W(E)⊕Emb(q)\mathbf{W}(E) \oplus \text{Emb}(q)W(E)⊕Emb(q)

投影后的向量占据一个token位置，与查询的词嵌入拼接后送入LLM。投影器仅占模型总参数的0.46%（Mistral-7B场景下），训练时LLM和检索器都冻结，只训练投影器。

训练分两阶段：

释义预训练：给定压缩token，让模型恢复出原文档文本------相当于教LLM"读懂"这个特殊token
上下文感知指令微调：在QA任务上微调，并用完整文档RAG作为教师做自蒸馏

这套方案在多个QA数据集上表现接近甚至超过传统RAG，同时把输入长度从175个token压到1个。

但，175倍压缩率的代价是什么？

这正是这篇论文要回答的问题。xRAG的投影器是一个固定容量的瓶颈，当文档信息量超过这个瓶颈所能承载的上限时，信息就会丢失。更关键的是，丢失的信息可能恰好是回答当前查询所需要的那部分。

🏗️ 方法详解：从"压力表"到"溢出检测器"

论文围绕三个研究问题（RQ）展开，层层递进：

研究问题	核心关切
RQ1	溢出在压缩表示中长什么样？有什么统计特征？
RQ2	能否不跑LLM推理，用轻量级方法高效检测溢出？
RQ3	只看压缩token够不够？还是必须结合查询信息？

溢出的形式化定义

作者给"溢出"下了个干净的操作性定义。设 M\mathcal{M}M 是冻结的LLM，C\mathcal{C}C 是压缩模块。对于一条样本 (qi,xi,ai)(q_i, x_i, a_i)(qi,xi,ai)（查询、上下文、答案），定义任务正确性指标 T\mathcal{T}T：

Oi={1,if T(无压缩)=1 且 T(有压缩)=00,otherwise\mathcal{O}_i = \begin{cases} 1, & \text{if } \mathcal{T}(\text{无压缩}) = 1 \text{ 且 } \mathcal{T}(\text{有压缩}) = 0 \\ 0, & \text{otherwise} \end{cases}Oi={1,0,if T(无压缩)=1 且 T(有压缩)=0otherwise

翻译成人话：如果模型看完整文档能答对，看压缩token答错了，那就是溢出。 这个定义很巧妙地排除了"文档本身就没有答案"和"模型本来就不会"的干扰。

第一层检测：上下文复杂性度量（查询无关）

最朴素的想法：文档越复杂、越长，压缩就越容易丢信息。作者测试了三个指标：

上下文长度 NctxN_{ctx}Nctx：原始token数量，越长越难压
语言模型困惑度 PPL：内容越"出人意料"，越难压缩
统计可压缩性 RiR_iRi：用gzip压缩比衡量，重复内容多的文档压缩比高

这些指标完全不看查询，纯粹衡量"文档本身有多难压"。

第二层检测：Token饱和统计（查询无关）

更进一步，直接分析压缩后的token向量的统计特性。作者假设：溢出的token会像噪声，而信息保留完好的token应该有结构化的能量分布。

三个统计量：

Hoyer稀疏度------衡量向量能量是否集中在少数维度上。信息丰富的token通常稀疏度更高（能量集中），而溢出的token能量分散，趋近均匀分布。

谱熵------对向量做离散余弦变换（DCT），然后计算能量分布的熵。低熵意味着能量集中在几个频率分量上（有结构），高熵接近白噪声。这就好比听音乐和听收音机的"沙沙"声------前者有明确的频率结构，后者是均匀噪声。

峰度------衡量分布的"尖峰胖尾"程度。高斯分布的峰度为0，高峰度说明有少数维度值特别大。溢出token的维度值趋于均匀，峰度趋近0。

第三层检测：注意力特征（查询感知，需LLM推理）

这一层需要跑LLM的前向传播，分析模型在生成答案时如何"关注"压缩token：

对压缩token的平均注意力权重：如果模型几乎不看这个token，说明信息可能已经丢了
注意力比率：压缩token vs 普通token获得的注意力比值
注意力熵：注意力分布越散，说明模型越"困惑"

核心武器：学习型探测分类器

前面的手工特征效果有限（后面实验会看到），真正起作用的是基于表示的学习探测（Learned Probing）。

作者从不同阶段提取查询和上下文的嵌入向量，构建联合特征：

ϕi=[xi(sc);qi(sq)]\phi_i = [x_i^{(s_c)}; q_i^{(s_q)}]ϕi=[xi(sc);qi(sq)]

其中 scs_csc 和 sqs_qsq 分别是上下文和查询的表示阶段（预投影、后投影、LLM中间层、LLM最后层）。

三种分类器架构：

线性探针：测试溢出是否线性可分
MLP探针：引入非线性交互
MLP + 监督对比学习（SCL）：混合损失函数，推动同类样本聚拢、异类样本远离

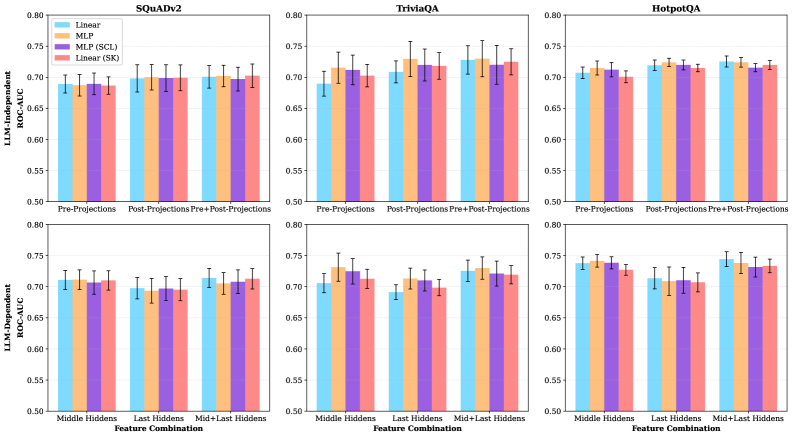
图1：不同分类器架构和特征组合的溢出检测性能（ROC-AUC）。上排是LLM-Independent（不依赖LLM推理），下排是LLM-Dependent（使用LLM隐藏层状态）。三列对应SQuADv2、TriviaQA和HotpotQA三个数据集。可以看到上下两排的性能基本持平，说明LLM推理并未提供额外信号。

🧪 实验设置与结果

实验配置

配置项	具体设置
基座LLM	xRAG-7B（基于Mistral-7B-Instruct-v0.2）
检索器	SFR-Embedding-Mistral
数据集	SQuADv2, TriviaQA, HotpotQA
评估指标	ROC-AUC（溢出检测是二分类任务）
数据筛选	仅保留无压缩时能正确回答的样本

数据筛选这一步值得注意：作者过滤掉了"模型本来就答不对"的样本，确保研究的是纯粹由压缩引起的性能下降。

主结果（Table 1）

检测阶段	特征类型	TriviaQA	SQuADv2	HotpotQA	说明
压缩前	上下文复杂性	0.589	0.605	0.541	长度、PPL等，几乎不管用
推理前	饱和统计	0.568	0.529	0.533	能分辨token类型，但预测不了溢出
推理前	联合表示探测	0.725	0.703	0.720	不需要跑LLM，平均AUC 0.72
推理后	联合表示探测	0.719	0.713	0.733	跑了LLM反而没提升
推理后	注意力特征	0.589	0.599	0.576	注意力特征帮助不大

RQ1：溢出长什么样？

饱和统计是个好工具，但用错了场景。

作者发现了一个有趣的"分离悖论"：谱熵、峰度等饱和统计量可以极其准确地区分xRAG压缩token和普通文本token（AUC > 0.95，接近完美分类）。压缩token的谱熵比文本token低7-14%，峰度高35-87%------它们在统计上确实长得不一样。

但对于区分"溢出的压缩token"和"没溢出的压缩token"，这些统计量几乎无能为力（AUC仅0.52-0.58，和抛硬币差不多）。

这说明什么？溢出不是压缩token本身的"体质问题"，而是压缩token与特定查询之间的"匹配问题"。 同一个压缩token，对于问题A可能信息足够，对于问题B就不够用了。就像同一个行李箱，装冬天的衣服可能塞不下，但装夏天的衣服绰绰有余。

RQ2：能不能不跑LLM就检测溢出？

能，而且跑了LLM也没有额外收益。

学习探测分类器在后投影阶段（xRAG投影器输出之后、LLM前向传播之前）就达到了平均0.72的AUC。这意味着压缩造成的信息损失在投影完成的那一刻就已经"写在脸上"了。

更有意思的是，使用LLM中间层甚至最后层的隐藏状态来做检测，性能并没有提升（从图1可以看到上下两排的柱状图高度基本一致）。LLM的深层处理并没有把溢出信号放大或改变。

这对工程落地来说是个好消息：检测器可以作为LLM推理的前置门控（pre-LLM gate），计算开销几乎可以忽略不计。

RQ3：必须看查询吗？

必须。

联合查询-上下文表示模型（0.70-0.73 AUC）显著优于仅使用上下文表示的模型（0.64-0.69 AUC）。差距不算巨大但统计上显著，而且在所有三个数据集上一致。

更值得玩味的是：线性分类器的表现和MLP差不多。 这意味着在联合表示空间中，溢出和非溢出样本大致可以用一个超平面分开------溢出信号有简单的线性结构，不需要复杂的非线性建模就能捕捉。

消融实验细节

从图1还能读出几个有价值的细节：

Pre-Projections vs Post-Projections：在LLM-Independent场景下（上排），Post-Projections略优于Pre-Projections，说明xRAG投影器在映射过程中引入了某些有助于溢出区分的信号变化。
监督对比学习（SCL）没有明显帮助：MLP(SCL)的柱子并没有显著高于普通MLP。这可能是因为数据量有限，SCL的正则化效果被稀疏样本的方差掩盖了。
数据集差异：HotpotQA上的性能整体更好（0.72-0.73），这可能是因为多跳推理任务对信息完整性更敏感，溢出的"症状"更明显。

🔬 深入讨论：为什么这个问题重要？

软压缩的信任问题

xRAG号称175倍压缩、性能不降，但这是在测试集平均意义上的。落到每一条具体查询上，有多大比例会因为压缩而答错？论文的数据告诉我们：这个比例不可忽视。 否则溢出检测就没有研究的必要了。

这揭示了一个更深层的问题：压缩模型的平均性能掩盖了个体层面的不可靠性。 如果你部署xRAG来做客服问答，用户问10个问题，可能有7个答得很好，但剩下3个因为溢出给了完全错误的答案。而你无法从平均指标中预见这一点。

和信息瓶颈理论的联系

论文没有显式提到信息瓶颈（Information Bottleneck），但溢出本质上就是一个信息瓶颈问题。xRAG的投影器把高维文档表示映射到固定维度的"瓶颈"，信息论告诉我们这个过程必然有信息损失。问题不在于"有没有信息损失"------答案是一定有------而在于"损失的是不是任务关键信息"。

这也解释了为什么查询无关的检测方法效果差：信息损失是与查询无关的（取决于压缩器和文档），但损失是否致命是与查询相关的。

和多模态模型的类比

xRAG把检索文档当作一种"模态"，用投影器做模态融合------这和LLaVA等多模态模型的思路如出一辙。LLaVA用一个投影器把视觉编码器的输出映射到语言模型空间，xRAG用同样的方式处理检索嵌入。

那么一个自然的追问是：多模态模型中是否也存在类似的"视觉溢出"？ 当图片信息过于复杂时，投影器的固定容量可能也无法完整传递所有视觉细节。这篇论文的检测方法或许可以迁移过去。

💡 实际工程启示

自适应压缩策略

0.72的AUC听起来不算高，但已经足够支撑一种实用的架构模式：

复制代码

检索文档 → xRAG压缩 → 溢出检测器
                              ├── 不溢出 → 用压缩token，省资源
                              └── 溢出 → 回退到完整文档

这种**自适应门控（Adaptive Gating）**策略可以在大部分"简单"查询上享受压缩带来的效率提升，只在"困难"查询上付出完整文档的计算代价。假设70%的查询不需要回退，系统整体仍然能获得可观的加速。

前置检测的成本

探测分类器本身有多轻？一个线性分类器就能达到和MLP接近的性能，计算量几乎可以忽略。即使使用MLP探针，相比一次LLM前向传播，开销也微不足道。

与其他压缩方法的适用性

论文只研究了xRAG，但检测思路应该可以推广到其他软压缩方法（如AutoCompressor、ICAE、Gist Tokens）。这些方法虽然不是压缩到一个token，但本质上都面临"压缩表示容量有限"的问题。差异只在于溢出发生的概率和阈值不同。

🤔 我的看法与局限性分析

0.72 AUC够不够？

坦白说，0.72的AUC在实际部署中还差点意思。假设溢出率为20%，0.72 AUC的检测器可能会漏掉相当一部分溢出案例，同时把一些正常的压缩token误判为溢出。

不过作为一篇Student Research Workshop论文，这项工作的价值更多在于问题定义而非解法本身。"Token溢出"这个概念的提出和形式化，比0.72还是0.82的AUC数字更有意义。后续工作可以在这个框架上继续改进检测器。

xRAG以外的适用范围

论文的实验全部在xRAG上做的，而xRAG的压缩比是极端的（175:1）。在更温和的压缩比（比如16:1的AutoCompressor）下，溢出可能更少发生，检测也可能更困难或更简单------这个问题留给了未来工作。

查询感知检测的矛盾

论文证明了"必须看查询才能有效检测溢出"，但在真实RAG pipeline中，查询在检索阶段就已经可用了。真正的工程问题不是"要不要看查询"，而是：你已经有了查询，为什么不直接用查询来判断该不该压缩？ 比如，简单的事实查询（"什么时候成立的？"）可能只需要文档中的一个数字，压缩丢了不影响；但复杂推理查询需要文档的多个细节，压缩就容易出问题。一个基于查询复杂度的启发式方法可能比训练检测器更简单实用。

溢出标签的获取成本

溢出的ground truth标签需要同时跑"无压缩推理"和"有压缩推理"，然后比较结果。这意味着训练检测器需要大量的标注数据，而获取这些数据的代价不低。如何降低标注成本，或者做少样本/零样本的溢出检测，是一个值得探索的方向。

📊 关键结论回顾

发现	启示
饱和统计能区分token类型（AUC>0.95）但不能预测溢出	溢出是查询相关的，不是token本身的属性
联合表示探测在推理前就达到0.72 AUC	可以做低成本的前置门控
LLM推理不提供额外检测信号	压缩损失在投影完成时就已确定
线性分类器表现接近MLP	溢出信号在联合表示空间中结构简单

🔗 相关工作速览

方法	类型	压缩粒度	特点
xRAG (NeurIPS 2024)	软压缩	1个token/文档	极端压缩，投影器仅0.46%参数
AutoCompressor	软压缩	~50 tokens/段落	递归压缩，保留更多细节
ICAE	软压缩	可变	基于AE架构的上下文压缩
Gist Tokens	软压缩	固定gist长度	需要存储额外KV Cache
LLMLingua	硬压缩	变长	基于困惑度的token剪枝
FlexRAG	混合压缩	自适应	选择性压缩+重要性估计

这篇论文的独特之处在于：它不是在提出新的压缩方法，而是给现有压缩方法配上了一个安全阀。无论压缩方法多先进，都存在信息丢失的风险，检测机制才能让系统知道什么时候该"放弃压缩"。

📝 总结

这篇论文切入了一个被普遍忽视的问题：软压缩方法在什么时候会失效？ 通过严格定义Token溢出、系统性地比较从查询无关到查询感知的检测方法，作者揭示了几个有价值的洞察：

压缩token在统计特征上确实和普通token不一样，但这种差异不等于溢出
溢出是一个查询条件化的现象------同一个压缩token对不同查询的可用性不同
溢出信号在压缩完成那一刻就可以被捕捉，不需要等LLM处理完

对于正在考虑在RAG系统中使用软压缩的工程师来说，这篇论文传递了一个明确的信息：压缩可以用，但需要配合检测机制来兜底。 盲目相信压缩后的表示，就像把所有行李都塞进一个登机箱然后不检查拉链------迟早会在飞机上"炸开"。