文章目录
- 线索栏
- 笔记栏
-
- [1. 核心概念:零扩展 vs. 符号扩展](#1. 核心概念:零扩展 vs. 符号扩展)
-
- 1)目标
- [2)无符号数 → 更大类型(零扩展)](#2)无符号数 → 更大类型(零扩展))
- [3)补码数 → 更大类型(符号扩展)](#3)补码数 → 更大类型(符号扩展))
- 2.代码示例与深度分析
- 3.练习题
- 总结栏
线索栏
- 将一个较小的整数类型转换为较大的类型时,无符号数和有符号数(补码) 分别采用什么方法?
- 零扩展和符号扩展的具体操作是什么?它们的数学原理(转换公式)是什么?
- 示例代码中,short sx = -12345和 unsigned short usx = sx在内存中的位模式相同吗?为什么?
- 当将它们分别转换为 int和 unsigned后(x和ux),输出的字节序列有何不同?这说明了什么?
- C语言标准对于类型转换顺序(改变大小 vs. 改变有符号性)有何规定?
- (练习题2.23)移位操作 (word << 24) >> 24在有符号和无符号语境下(fun1vs fun2)有何本质区别?
笔记栏
1. 核心概念:零扩展 vs. 符号扩展
1)目标
在不同字长的整数间转换,保持数值不变。
2)无符号数 → 更大类型(零扩展)
在二进制表示的高位(左侧)添加0。
(1)原理公式:若 u ⃗ = [ u w − 1 , ⋯ , u 0 ] \vec{u}=[u_{w−1},⋯,u_0 ] u =[uw−1,⋯,u0], u ' ⃗ = [ 0 , ⋯ , 0 , u w − 1 , ⋯ , u 0 ] \vec{u'}=[0,⋯,0,u_{w−1} ,⋯,u_0] u' =[0,⋯,0,uw−1,⋯,u0],则 B 2 U w ( u ⃗ ) = B 2 U w ' ( u ' ⃗ ) B2U_w(\vec{u})=B2U_w'(\vec{u'}) B2Uw(u )=B2Uw'(u' )。
(2)直观理解:正数的二进制表示不会因高位补零而改变数值。
3)补码数 → 更大类型(符号扩展)
在二进制表示的高位(左侧)添加符号位(最高有效位的副本)。
(1)原理公式: x ⃗ = [ x w − 1 , ⋯ , x 0 ] \vec{x}=[x_{w−1},⋯,x_0 ] x =[xw−1,⋯,x0], x ' ⃗ = [ 0 , ⋯ , 0 , x w − 1 , ⋯ , u 0 ] \vec{x'}=[0,⋯,0,x_{w−1} ,⋯,u_0] x' =[0,⋯,0,xw−1,⋯,u0],则 B 2 U w ( x ⃗ ) = B 2 U w ' ( x ' ⃗ ) B2U_w(\vec{x})=B2U_w'(\vec{x'}) B2Uw(x )=B2Uw'(x' )。
(2)直观理解:为保持负数(符号位为1)的负权重不变,必须复制符号位填充新增高位。图2-20的条形图用颜色块(负权重)直观展示了这一原理。
(3)推导证明:通过归纳法证明扩展一位(w+1)保持数值不变。关键在于权重关系: − 2 w + 2 w − 1 = − 2 w − 1 −2^w+2^{w−1}=−2^{w−1} −2w+2w−1=−2w−1
2.代码示例与深度分析
c
short sx = -12345; /* 补码: 0xCFC7 */
unsigned short usx = sx; /* 无符号: 0xCFC7 (53191) */
int x = sx; /* 符号扩展: 0xFFFFCFC7 (-12345) */
unsigned ux = usx; /* 零扩展: 0x0000CFC7 (53191) */(1)关键观察1:sx 和 usx 的16位位模式完全相同(均为 0xCFC7),但解释不同(-12345 vs 53191)。这再次验证了"位+上下文"。
(2)关键观察2:转换为32位后,x 的位模式为 0xFFFFCFC7(符号扩展),ux 的位模式为 0x0000CFC7(零扩展)。相同源位模式,因上下文(类型)不同,采用了完全不同的扩展方式,导致最终32位模式截然不同。
(3)重要规定(C标准):当同时涉及改变数据大小和有/无符号转换时,标准规定先改变大小(进行符号/零扩展),再改变有符号性。
(unsigned) sx 等价于 (unsigned) (int) sx(先符号扩展为int,再将结果解释为无符号数),而非 (unsigned) (unsigned short) sx。
3.练习题
练习题2.22

通过对公式(2.3)的直接计算,验证 [1011], [11011], [111011] 均为-5的补码表示(后者是前者的符号扩展)。

练习题2.23
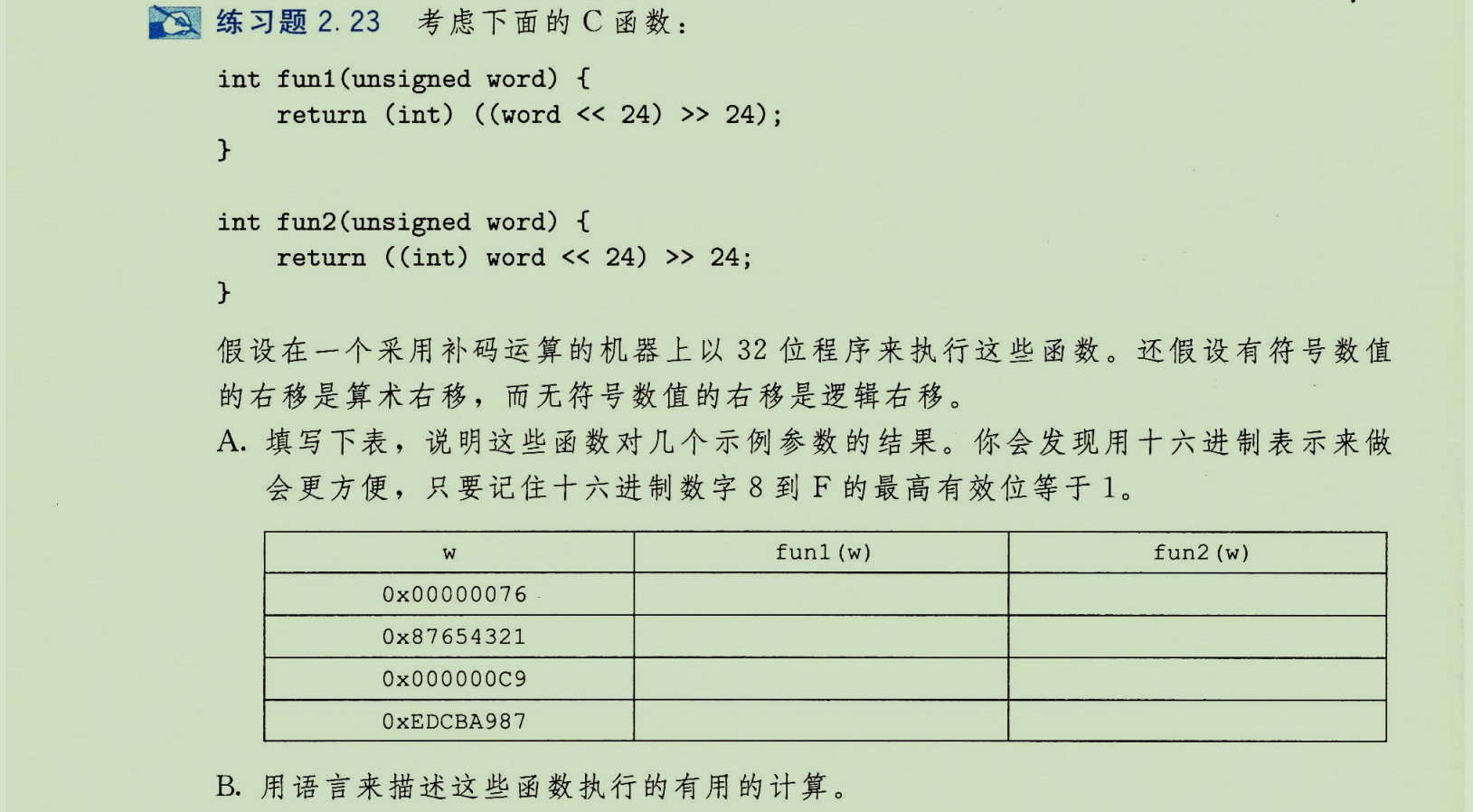
分析:
fun1:参数 word 类型为 unsigned。(word << 24) >> 24 全程为无符号运算(逻辑右移),结果转换为 int。此操作实质是提取低8位,并零扩展至32位(但随后被解释为有符号数)。
fun2:(int) word 先将无符号数 word 强制转换为 int(保持位模式,重新解释)。<<24 和 >>24 均为有符号运算(算术右移)。此操作实质是提取低8位,并进行符号扩展至32位。
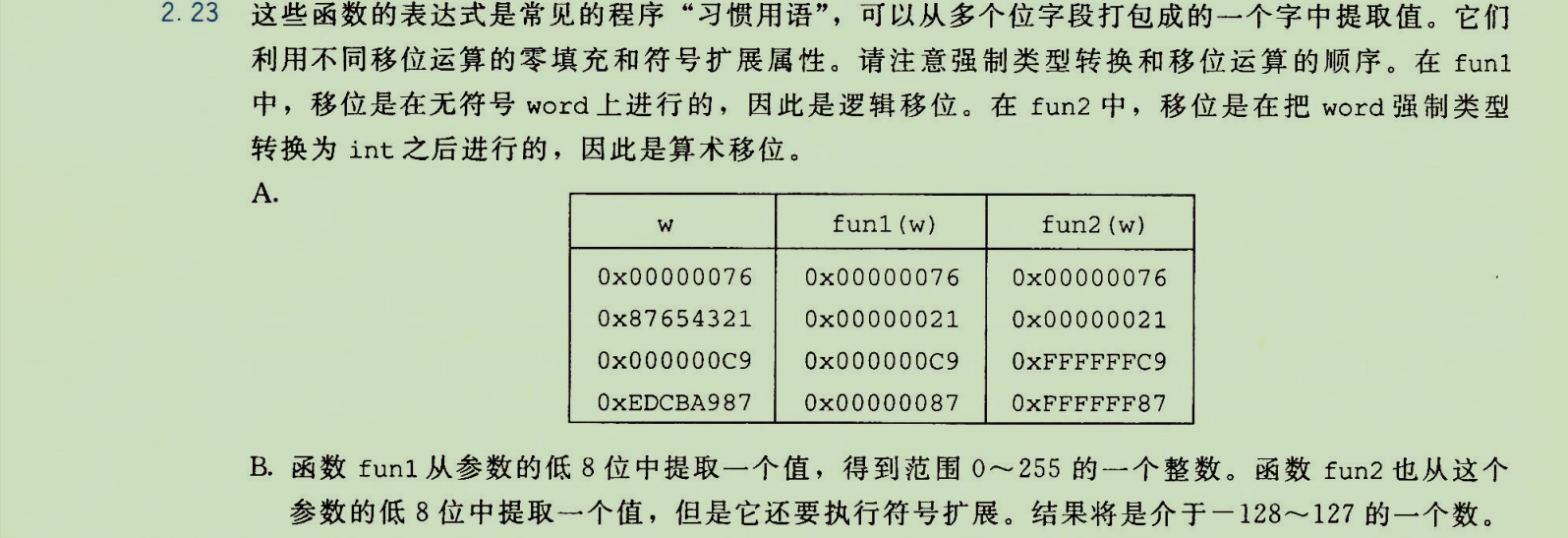
总结栏
本节核心是理解如何安全地将整数扩展为更大字长,关键在于符号性决定扩展规则:
- 两条铁律:
(1)无符号数 → 零扩展(高位补0)。
(2)补码数 → 符号扩展(高位补符号位副本)。 - 底层原理:扩展是为了在改变表示宽度的同时,保持数学值不变。符号扩展的归纳法推导严谨地证明了这一点。
- 转换顺序至关重要:C语言规定,混合转换时先改变大小(应用扩展规则),再处理有/无符号转换。忽略此顺序会导致程序行为与直觉相悖。
- 移位的双重语义:相同的C运算符(>>)在无符号和有符号语境下行为不同(逻辑右移 vs算术右移),这是理解fun1和fun2差异的关键。fun1实现零扩展提取字节,fun2实现符号扩展提取字节。
理解这些规则是进行安全类型转换、解析二进制数据(如网络封包、文件格式)以及编写可移植底层代码的基础。练习题2.23是对该知识点极佳的检验与应用。