论文地址:https://arxiv.org/abs/2509.24006
项目地址:https://github.com/thu-ml/SLA
发表时间:2025年11月19日

摘要
扩散Transformer(DiT)模型在视频生成任务中,因序列长、注意力机制二次计算复杂度,存在注意力延迟瓶颈。研究发现注意力权重可解耦为高秩大权重和低秩小权重矩阵,据此提出稀疏-线性注意力机制(SLA)。
SLA将注意力权重分为核心、边缘、可忽略三类,分别采用标准注意力(O(N2)O(N^2)O(N2))、线性注意力(O(N)O(N)O(N))计算及跳过计算,整合于单个GPU核函数,支持前向与反向传播,仅需少量微调。
实验表明,SLA可减少95%注意力计算量(等效降低20倍),不损失生成质量且性能优于基线;在Wan2.1-1.3B模型上,注意力计算速度提升13.7倍,视频生成端到端速度提升2.2倍。
1 引言
注意力机制(Vaswani等人,2017)是Transformer中唯一具有二次计算复杂度的操作,其余操作计算量与序列长度NNN呈线性关系。DiT模型(Peebles和Xie,2022)在视频生成任务中,序列长度通常为1万至10万,注意力机制成为主要计算瓶颈,因此降低其计算成本对提升模型效率至关重要。
目前适用于DiT的高效注意力方法主要分为两类:(1)稀疏注意力方法,仅计算部分注意力分数;(2)线性注意力方法,通过重构运算将计算复杂度降至O(N)O(N)O(N)。
现有方法的局限性
两类方法在大幅降低注意力计算量方面均有挑战:
(L1)线性注意力在视频扩散模型中效果不佳,相关研究少且局限于图像生成,应用于视频生成会导致质量严重下降。
(L2)稀疏注意力难以实现超高稀疏度且耗资源;序列长度低于5万时,稀疏度仅40%~ 60%,现有高稀疏度(80%~ 85%)结果仅适用于极长序列(10万~30万)。
核心发现
DiT的注意力权重可分解为少量高秩大权重和绝大部分极低秩权重;该发现给出优化策略------高秩大权重采用稀疏加速,低秩权重采用低秩加速。
本文方法
本文提出适用于DiT的可训练混合稀疏-线性注意力机制(SLA):将注意力权重分块并动态划分为核心、边缘、可忽略三类,核心块用FlashAttention精确计算,边缘块用线性注意力计算,可忽略块直接跳过;该设计将稀疏度提升至95%,且线性注意力计算成本极低(不足标准注意力的0.5%)。此外,SLA实现了高效前向和反向传播,仅需少量微调即可兼顾生成质量与计算效率。
实验结果
在Wan2.1-1.3B模型(3万序列长度)上,SLA可减少95%注意力计算量且不降低视频生成质量;注意力核函数速度提升13.7倍,端到端速度提升2.2倍,注意力计算耗时可忽略,在生成质量和效率上均优于所有基线方法。
2 预备知识
2.1 分块稀疏注意力
给定查询矩阵QQQ、键矩阵KKK和值矩阵VVV(均属于RN×d\mathbb{R}^{N×d}RN×d),标准注意力机制先计算分数矩阵S=QK⊤/dS=QK^\top/\sqrt{d}S=QK⊤/d ,再通过Softmax函数得到注意力权重矩阵PPP,最终输出O=PVO=PVO=PV。当序列长度NNN较大时,该方法因需执行O(N2d)O(N^2d)O(N2d)次运算而效率低下。
稀疏注意力的核心思路是基于P得到掩码矩阵MMM(属于{0,1}N×N\{0,1\}^{N×N}{0,1}N×N)对注意力权重进行掩码处理,减少计算量,即P←P⊙MP←P⊙MP←P⊙M(⊙⊙⊙为按元素乘积)。常用策略为设置阈值τττ,当Pij>τP_{ij}>τPij>τ时,令Mij=1M_{ij}=1Mij=1;当Mij=0M_{ij}=0Mij=0时,可直接跳过QiKj⊤Q_iK_j^\topQiKj⊤和PijVjP_{ij}V_jPijVj的计算(其中Qi=Q[i,:]Q_i=Q[i,:]Qi=Q[i,:],Kj=K[j,:]K_j=K[j,:]Kj=K[j,:],Vj=V[j,:]V_j=V[j,:]Vj=V[j,:])。
但逐元素的稀疏注意力在现代GPU上效率较低,实际实现(如FlashAttention,Dao,2023)均采用分块方式。具体而言,稀疏FlashAttention先将Q、K、V、S、P、MQ、K、V、S、P、MQ、K、V、S、P、M划分为若干分块{Qi}、{Kj}、{Vj}、{Sij}、{Pij}、{Mij}\{Q_i\}、\{K_j\}、\{V_j\}、\{S_{ij}\}、\{P_{ij}\}、\{M_{ij}\}{Qi}、{Kj}、{Vj}、{Sij}、{Pij}、{Mij},其中Qi∈Rbq×dQ_i∈\mathbb{R}^{b_q×d}Qi∈Rbq×d,Kj、Vj∈Rbkv×dK_j、V_j∈\mathbb{R}^{b_{kv}×d}Kj、Vj∈Rbkv×d,Sij、Pij、Mij∈Rbq×bkvS_{ij}、P_{ij}、M_{ij}∈\mathbb{R}^{b_q×b_{kv}}Sij、Pij、Mij∈Rbq×bkv。每个分块掩码MijM_{ij}Mij内的元素均为0或1,当Mij[:,:]=0M_{ij}[:,:]=0Mij[:,:]=0时,直接跳过QiKj⊤Q_iK_j^\topQiKj⊤和PijVjP_{ij}V_jPijVj的计算。
2.2 线性注意力
线性注意力方法将标准注意力的计算复杂度从O(N2d)O(N^2d)O(N2d)降至O(Nd2)O(Nd^2)O(Nd2),其核心思路是引入特征映射ϕ(⋅)\phi(·)ϕ(⋅)作用于QQQ和KKK,解耦Softmax操作。具体而言,该方法将标准注意力中的权重替换为ϕ(Q)ϕ(K)⊤rowsum(ϕ(Q)ϕ(K)⊤)\frac{\phi(Q)\phi(K)^\top}{rowsum(\phi(Q)\phi(K)^\top)}rowsum(ϕ(Q)ϕ(K)⊤)ϕ(Q)ϕ(K)⊤,通过重构矩阵乘法顺序减少计算量:无需显式计算注意力权重,先计算ϕ(K)⊤V\phi(K)^\top Vϕ(K)⊤V,再将该中间结果作用于ϕ(Q)\phi(Q)ϕ(Q),公式如下:
H=ϕ(K)⊤V,Z=rowsum(ϕ(K)⊤)∈Rd×1,O=ϕ(Q)Hϕ(Q)Z.H=\phi(K)^\top V, Z=rowsum\left(\phi(K)^\top\right)∈\mathbb{R}^{d×1}, O=\frac{\phi(Q)H}{\phi(Q)Z}.H=ϕ(K)⊤V,Z=rowsum(ϕ(K)⊤)∈Rd×1,O=ϕ(Q)Zϕ(Q)H.
特征映射ϕ(⋅)\phi(·)ϕ(⋅)通常为激活函数。该形式无需显式构建N×NN×NN×N的矩阵SSS和PPP,实现了线性的计算复杂度。
3 研究动机与分析
3.1 SLA的设计动机
由于Softmax算子的特性,注意力权重矩阵PPP的元素取值范围为[0,1][0,1][0,1],且每行元素之和为1。此外,受Softmax指数缩放的影响,PPP中仅有小部分元素值相对较大,绝大部分元素值接近0 。图1(左)为从Wan2.1模型中采样得到的注意力权重典型分布,核心发现有二:(1)仅约8.1%的权重值大于平均值1/N1/N1/N;(2)相当一部分权重值极小,本文实验中约45%的权重值低于1/(100N)1/(100N)1/(100N)。
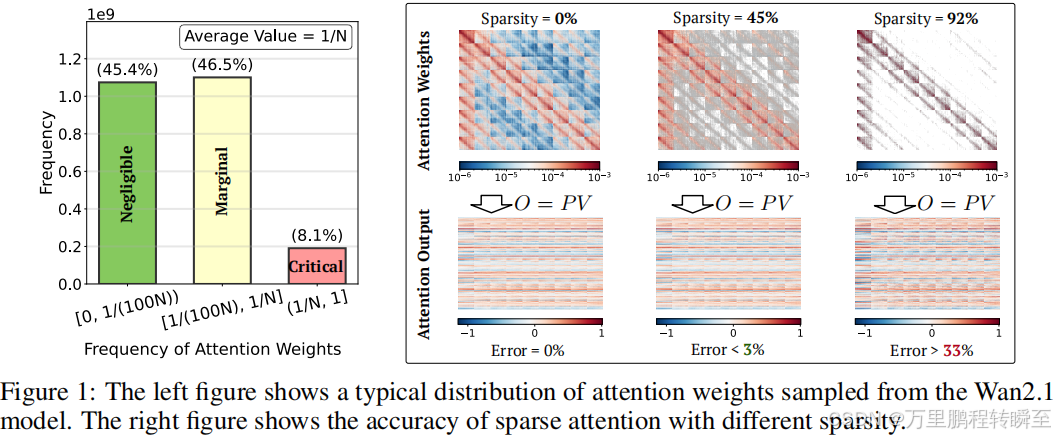
图1(右)所示,在稀疏注意力中跳过这45%的极小权重(即令掩码矩阵$M$中对应位置为0),与标准注意力的输出相比,相对L1误差不足3%;而仅保留8.1%的最大权重(稀疏度92%)时,误差会急剧上升至约33%。这一结果解释了为何现有稀疏注意力方法的稀疏度难以突破90%。
权重值介于1/(100N)1/(100N)1/(100N)和1/N1/N1/N之间的部分(图1中黄色柱体)成为研究难点:忽略该部分会导致精度显著损失,而采用标准注意力计算则会大幅降低稀疏度。所幸该部分权重的重要性远低于最大权重,这一发现促使本文将注意力权重划分为核心、边缘和可忽略三类:
- 核心权重主导注意力分布,采用稀疏FlashAttention计算输出;
- 可忽略权重直接跳过计算;
- 边缘权重则采用线性注意力处理,将计算复杂度降至O(Nd2)O(Nd^2)O(Nd2),提升稀疏注意力的性能。
实证结果 :图2展示了Wan2.1模型在不同注意力方法微调后的视频生成效果,包括纯线性注意力、稀疏度90%的纯稀疏注意力,以及稀疏度95%的SLA。由于线性注意力的计算成本几乎可忽略,SLA在95%稀疏度下的计算复杂度约为90%稀疏度纯稀疏注意力的一半(如在Wan2.1模型中,线性注意力的计算量不足标准注意力的0.5%)。实证结果表明,在视频生成质量上,SLA显著优于另外两种方法。

3.2 注意力权重分解:稀疏少部分,低秩大部分
研究发现 :如图3所示,标准注意力权重可解耦为两部分:(1)占比不足10%的子集,其秩与标准注意力权重接近 ;(2)占比超过90%的子集,其秩极低。由于注意力加速方法主要围绕稀疏性或低秩结构展开,这一发现给出自然且巧妙的优化策略------对前一部分采用稀疏注意力,对后一部分采用低秩近似。
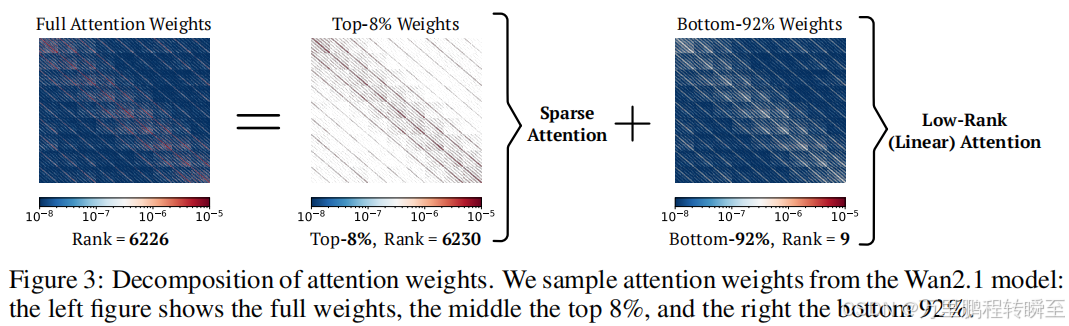
线性注意力此前应用效果不佳,主要原因是标准注意力权重具有高秩特性,而线性注意力的秩上限为ddd。图3(左)通过稳定秩的实例验证了这一点。研究发现,移除注意力权重矩阵PPP中的大值元素后,剩余矩阵呈现出极强的低秩特性。这促使本文通过稀疏掩码MMM对PPP进行分解:
P=P⊙M⏟稀疏分量+P⊙(1−M)⏟低秩分量.P=\underbrace{P⊙M}{稀疏分量}+\underbrace{P⊙(1-M)}{低秩分量}.P=稀疏分量 P⊙M+低秩分量 P⊙(1−M).
由于线性注意力本质上是注意力的低秩形式,因此可将低秩分量P⊙(1−M)P⊙(1-M)P⊙(1−M)替换为线性注意力。
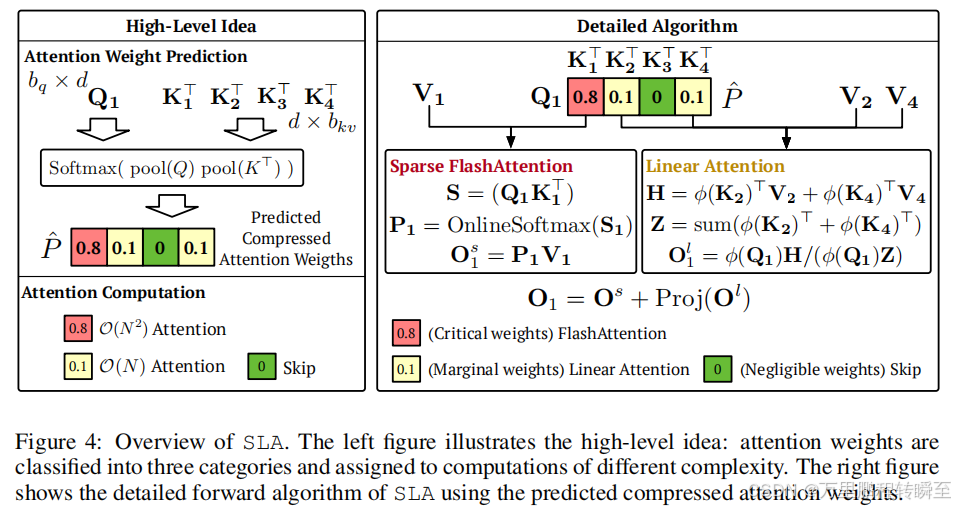
4 稀疏-线性注意力机制(SLA)
SLA将稀疏注意力与线性注意力有效整合至统一框架,实现二者的互补优化,尤其将两种注意力的计算融合至单个高效GPU核函数中。本节将详细介绍SLA的稀疏注意力和线性注意力组件。
SLA首先通过以下公式预测压缩的注意力权重矩阵Pc∈RN/bq×N/bkvP_c∈\mathbb{R}^{N/b_q×N/b_{kv}}Pc∈RN/bq×N/bkv:
Pc=Softmax(pool(Q)pool(K)⊤/d).(2)P_c=Softmax\left(pool(Q)pool(K)^\top/\sqrt{d}\right). \quad (2)Pc=Softmax(pool(Q)pool(K)⊤/d ).(2)
其中pool(⋅)pool(·)pool(⋅)为沿token维度的均值池化操作。随后,将PcP_cPc中的每个元素划分为三类,并将分类结果记录在压缩掩码矩阵Mc∈RN/bq×N/bkvM_c∈\mathbb{R}^{N/b_q×N/b_{kv}}Mc∈RN/bq×N/bkv中:排名前kh%k_h\%kh%的位置标记为核心(标签1),排名后kl%k_l\%kl%的位置标记为可忽略(标签-1),其余位置标记为边缘(标签0)。形式化定义如下:
Mc[i,j]={1,排名前kh%−1,排名后kl%0,其他情况.(3)M_c[i,j]=\begin{cases}1, & 排名前k_h\% \\ -1, & 排名后k_l\% \\ 0, & 其他情况\end{cases}. \quad (3)Mc[i,j]=⎩ ⎨ ⎧1,−1,0,排名前kh%排名后kl%其他情况.(3)
本文将根据McM_cMc的标签,对不同分块采用不同的计算方法。
4.1 SLA中的稀疏注意力
在掩码矩阵McM_cMc的引导下,采用稀疏FlashAttention计算稀疏注意力输出 。对于每个查询分块QiQ_iQi,遍历所有键、值分块Kj、VjK_j、V_jKj、Vj(j=0,...,N/bkvj=0,...,N/b_{kv}j=0,...,N/bkv),当Mc[i,j]=1M_c[i,j]=1Mc[i,j]=1时,执行以下计算:
Sij=QiKj⊤/d, Pij=OnlineSoftmax(Sij), Ois=Ois+PijVj.(4)S_{ij}=Q_iK_j^\top/\sqrt{d},\space P_{ij}=OnlineSoftmax(S_{ij}), \space O_i^s=O_i^s+P_{ij}V_j. \quad (4)Sij=QiKj⊤/d , Pij=OnlineSoftmax(Sij), Ois=Ois+PijVj.(4)
其中,OnlineSoftmax(·)算子以分块方式计算矩阵的Softmax值(实现细节见算法1的10-11行)。每个OisO_i^sOis的初始值设为0,算法1描述了稀疏注意力组件的前向计算过程,其最终输出记为OsO^sOs。
4.2 SLA中的线性注意力
基于低秩近似的思路,将公式1中的低秩分量P⊙(1−M)P⊙(1-M)P⊙(1−M)替换为2.2节介绍的线性注意力,形式如下:
ϕ(Q)ϕ(K)⊤rowsum(ϕ(Q)ϕ(K)⊤)⊙(1−M).\frac{\phi(Q)\phi(K)^\top}{rowsum\left(\phi(Q)\phi(K)^\top\right)}⊙(1-M).rowsum(ϕ(Q)ϕ(K)⊤)ϕ(Q)ϕ(K)⊤⊙(1−M).
具体而言,McM_cMc中标签为0的位置对应采用线性注意力处理的分块。对于每个查询分块QiQ_iQi,其线性注意力输出计算如下:
Hi=∑j:Mc[i,j]=0ϕ(Kj)⊤Vj,Zi=∑j:Mc[i,j]=0rowsum(ϕ(Kj)⊤),Oil=ϕ(Qi)Hiϕ(Qi)Zi.(5)H_i=\sum_{j:M_c[i,j]=0}\phi(K_j)^\top V_j, Z_i=\sum_{j:M_c[i,j]=0}rowsum\left(\phi(K_j)^\top\right), O_i^l=\frac{\phi(Q_i)H_i}{\phi(Q_i)Z_i}. \quad (5)Hi=j:Mc[i,j]=0∑ϕ(Kj)⊤Vj,Zi=j:Mc[i,j]=0∑rowsum(ϕ(Kj)⊤),Oil=ϕ(Qi)Ziϕ(Qi)Hi.(5)
如2.2节所述,ϕ(⋅)\phi(·)ϕ(⋅)为激活函数,Hi∈Rd×dH_i∈\mathbb{R}^{d×d}Hi∈Rd×d、Zi∈Rd×1Z_i∈\mathbb{R}^{d×1}Zi∈Rd×1为与H、ZH、ZH、Z类似的中间结果。算法1描述了线性注意力组件的前向传播过程,其最终输出记为OlO^lOl。
最终,SLA的整体注意力输出定义为:
O=Os+Proj(Ol).(6)O=O^s+Proj\left(O^l\right). \quad (6)O=Os+Proj(Ol).(6)
其中ProjProjProj为可学习的线性变换(Rd→Rd\mathbb{R}^d→\mathbb{R}^dRd→Rd),对OlO^lOl进行投影可有效降低Softmax注意力与线性注意力之间的分布失配问题 。该投影的计算复杂度为O(Nd2)O(Nd^2)O(Nd2),与OlO^lOl的计算复杂度一致,远低于标准注意力O(N2d)O(N^2d)O(N2d)的计算量。
核心见解:SLA中的线性注意力并非对边缘注意力权重对应的输出进行近似,而是作为一种可学习的补偿项,提升稀疏注意力的效果。这是因为单独的线性注意力难以准确近似标准注意力的输出,因此需要对目标模型的参数进行微调,使其适配线性注意力的使用。
5 基于SLA的模型微调
将SLA应用于扩散模型的流程十分简洁:直接将模型原有的注意力机制替换为SLA,并在与预训练数据一致的数据集上对模型进行少量步骤的微调。本节将详细介绍SLA的前向和反向传播过程,此外,附录A.3还将阐述SLA的其他效率优化策略。
5.1 前向传播
SLA前向计算的公式已在第4节介绍,完整的前向传播算法见算法1。值得注意的是,本文对每个键-值分块对(Kj,Vj)(K_j,V_j)(Kj,Vj)预计算hj=ϕ(Kj)⊤Vjh_j=\phi(K_j)^\top V_jhj=ϕ(Kj)⊤Vj和zj=rowsum(ϕ(Kj)⊤)z_j=rowsum(\phi(K_j)^\top)zj=rowsum(ϕ(Kj)⊤)(算法1第4行)。该设计确保当Mc[i,j]=0M_c[i,j]=0Mc[i,j]=0时,对应操作仅需一次矩阵加法(算法1第13行),大幅提升计算效率。为简化符号,后续将Qϕ=ϕ(Q)Q^\phi=\phi(Q)Qϕ=ϕ(Q)、Kϕ=ϕ(K)K^\phi=\phi(K)Kϕ=ϕ(K)。

5.2 反向传播
SLA的反向传播同时计算稀疏和线性组件的梯度,并将二者融合至单个GPU核函数中,提升计算效率。
梯度符号说明 :前缀ddd用于表示梯度,例如dOsdO^sdOs、dOldO^ldOl分别为OsO^sOs、OlO^lOl关于损失函数ℓ\ellℓ的梯度。

稀疏注意力的梯度计算
输出梯度dOsdO^sdOs通过反向传播计算dQdQdQ、dKdKdK和dVdVdV,推导过程与FlashAttention(Dao,2023)一致。给定dOsdO^sdOs,反向传播计算如下:
{dPij=dOijsVj⊤,Dis=rowsum(dOis⊙Ois)dSij=Pij⊙(dPij−Dis)dQi=dSijKj,dKj=dSij⊤QidVj=Pij⊤dOis.\begin{cases}dP_{ij}=dO_{ij}^sV_j^\top, D_i^s=rowsum(dO_i^s⊙O_i^s) \\ dS_{ij}=P_{ij}⊙(dP_{ij}-D_i^s) \\ dQ_i=dS_{ij}K_j, dK_j=dS_{ij}^\top Q_i \\ dV_j=P_{ij}^\top dO_i^s\end{cases}.⎩ ⎨ ⎧dPij=dOijsVj⊤,Dis=rowsum(dOis⊙Ois)dSij=Pij⊙(dPij−Dis)dQi=dSijKj,dKj=dSij⊤QidVj=Pij⊤dOis.
其中Dis∈Rbq×1D_i^s∈\mathbb{R}^{b_q×1}Dis∈Rbq×1为列向量。
线性注意力的梯度计算
梯度dOldO^ldOl通过链式法则推导得到dQϕdQ^\phidQϕ、dKϕdK^\phidKϕ和dVdVdV,公式如下:
dHi=(QiϕQiϕZi)⊤dOil,Dil=rowsum(dOil⊙Oil),dZi=−(QiϕQiϕZi)⊤DildQiϕ=(dOil(Hi)⊤−DilZi⊤)QiϕZi,dKjϕ=Vj(dHi)⊤+(dZi)⊤,dVj=KjϕdHi.\begin{aligned} & dH_i=\left(\frac{Q_i^\phi}{Q_i^\phi Z_i}\right)^\top dO_i^l, D_i^l=rowsum\left(dO_i^l⊙O_i^l\right), dZ_i=-\left(\frac{Q_i^\phi}{Q_i^\phi Z_i}\right)^\top D_i^l \\ & dQ_i^\phi=\frac{\left(dO_i^l(H_i)^\top-D_i^l Z_i^\top\right)}{Q_i^\phi Z_i}, dK_j^\phi=V_j\left(dH_i\right)^\top+\left(dZ_i\right)^\top, dV_j=K_j^\phi dH_i \end{aligned}.dHi=(QiϕZiQiϕ)⊤dOil,Dil=rowsum(dOil⊙Oil),dZi=−(QiϕZiQiϕ)⊤DildQiϕ=QiϕZi(dOil(Hi)⊤−DilZi⊤),dKjϕ=Vj(dHi)⊤+(dZi)⊤,dVj=KjϕdHi.
其中dKjϕdK_j^\phidKjϕ和dVjdV_jdVj通过聚合所有dHidH_idHi和dZidZ_idZi得到。与前向传播类似,本文对每个dHidH_idHi和dZidZ_idZi进行预计算,使剩余计算简化为简单的矩阵加法,详细算法见算法2。
6 实验
6.1 实验设置
模型与数据集
本文主实验基于Wan2.1-1.3B模型(Wan等人,2025)开展视频生成实验,附录A.2则基于LightningDiT模型(姚等人,2025)开展图像生成实验。视频实验采用从Pexels、Common Crawl等网站收集的私有数据集,包含2万个480p分辨率、5秒时长的视频,用于模型微调;图像实验遵循LightningDiT的实验设置,采用512×512分辨率的ImageNet数据集。
基线方法
本文将SLA与适用于扩散模型的主流稀疏注意力方法对比,包括:(1)VSA(张等人,2025c);(2)VMoBa(吴等人,2025);(3)无需训练的SparseAttn(Sparge-F,张等人,2025a);(4)可训练的SparseAttn(Sparge-T,本文自行实现,因无官方实现版本)。此外,为开展消融实验,设计了以下基线方法:(5)纯线性注意力(Linear Only);(6)纯稀疏注意力(Sparse Only,仅使用SLA的稀疏注意力组件);(7)线性+稀疏直接融合(L+S,将纯线性和纯稀疏注意力的输出直接相加)。
评价指标
视频质量方面,遵循张等人(2024a)、杨等人(2025b)的设置,采用VBench(张等人,2024a)的四个评价维度:成像质量(IQ)、整体一致性(OC)、美学质量(AQ)、主体一致性(SC);同时采用视觉奖励值(VR,徐等人,2024)评估人类偏好,以及视频美学质量(VA)、视频技术质量(VT,刘等人,2023)。图像质量方面,遵循姚等人(2025)的设置,采用FID值。注意力计算复杂度采用浮点运算数(FLOPs)衡量;注意力效率采用每秒浮点运算数(FLOPS)评估核函数效率,其中FLOPS定义为O(标准注意力)/tO(标准注意力)/tO(标准注意力)/t(O(⋅)O(·)O(⋅)为运算量,ttt为注意力延迟);端到端生成延迟以秒为单位。
超参数
视频实验中,训练批次大小设为64,Wan2.1模型微调2000步;根据消融实验结果,激活函数ϕ\phiϕ选用Softmax,kh%=5%k_h\%=5\%kh%=5%,kl%=10%k_l\%=10\%kl%=10%,分块大小bq=bkv=64b_q=b_{kv}=64bq=bkv=64。图像生成任务的超参数详见附录A.2。
6.2 有效性验证
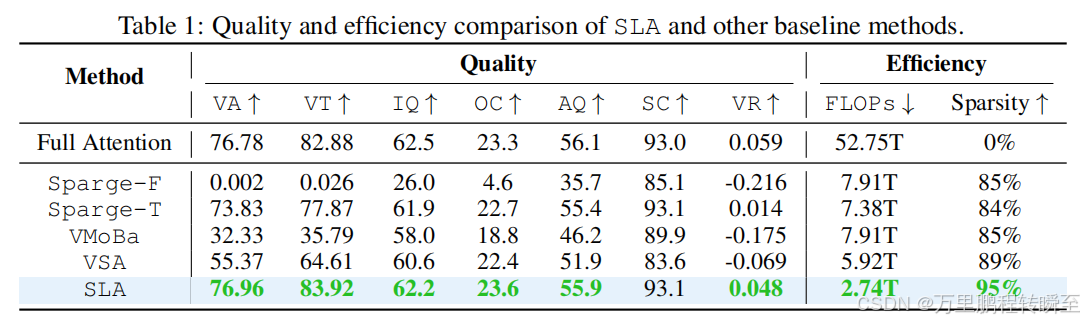
表1对比了Wan2.1-1.3B模型在SLA、标准注意力及各基线方法微调后的视频生成质量和效率。结果表明,SLA在保持与标准注意力相当的视频生成质量的同时,效率提升约19.3倍;且相较于基线方法,即使在更高的稀疏度下,SLA仍能实现更优的生成质量。例如,SLA在95%稀疏度下的效率约为85%稀疏度基线方法的3倍,且生成质量更优。
6.3 效率验证
图6对比了SLA与各基线方法在RTX5090显卡 上运行Wan2.1-1.3B模型的核函数速度和端到端延迟。需注意的是,VSA在89%稀疏度、VMoBa在85%稀疏度下的生成质量已低于SLA,因此更高稀疏度(如95%)的对比不具备质量可比性。
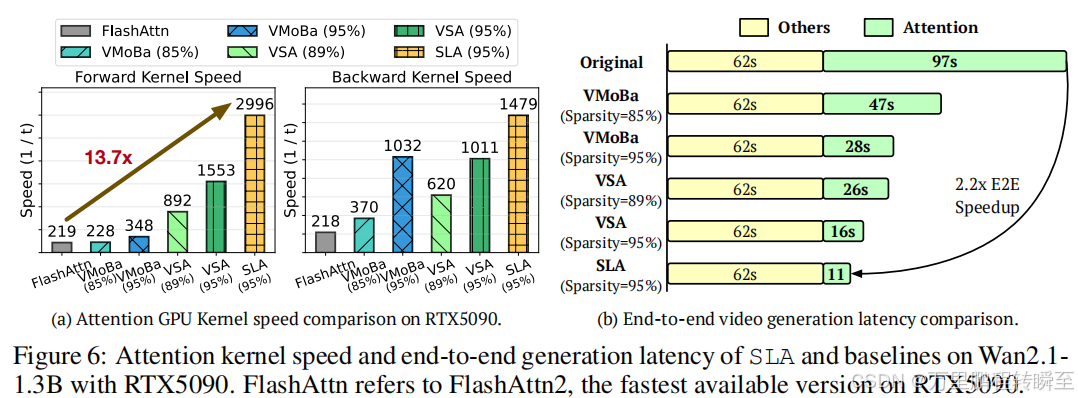
前向传播中,SLA的速度较FlashAttention2提升13.7倍,且比95%稀疏度的VSA快1.93倍、比95%稀疏度的VMoBa快3.36倍;反向传播中,SLA较FlashAttention2速度提升6.8倍,仍优于VSA和VMoBa。端到端视频生成中,SLA将注意力延迟从97秒降至11秒(降低8.8倍),实现2.2倍的端到端速度提升。
微调开销方面,本文对Wan2.1-1.3B模型仅进行了2000步、批次大小64的微调,计算成本不足预训练的0.1%(预训练通常为105~106步、批次大小103~104,Wan等人,2025)。
6.4 消融实验
稀疏与线性注意力的融合效果
为验证SLA融合稀疏和线性注意力的有效性,本文在Wan2.1模型上对比了SLA与纯稀疏、纯线性、线性+稀疏直接融合方法的端到端生成质量和效率。表2结果表明,SLA的生成质量最优,且效率高于纯稀疏和线性+稀疏直接融合方法,验证了本文融合策略的有效性。
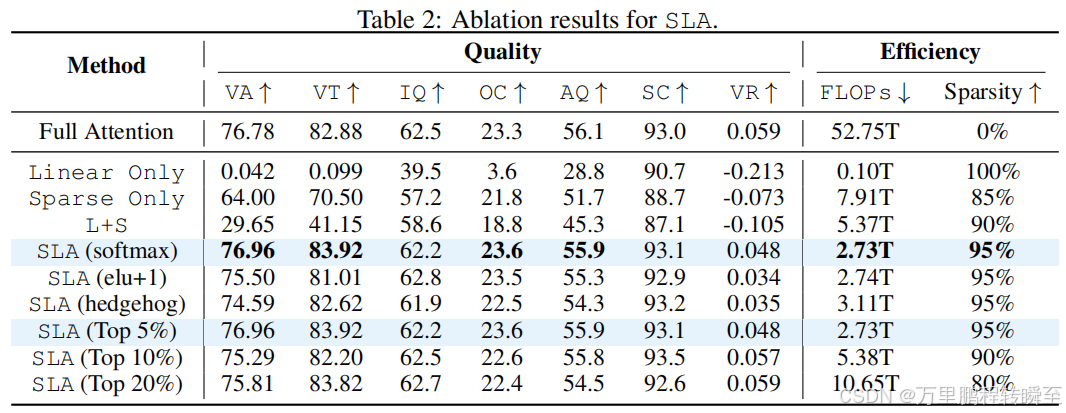
线性注意力中激活函数的影响
为研究线性注意力组件中激活函数ϕ\phiϕ的作用,本文测试了Softmax、ELU+1和Hedgehog三种激活函数。表2结果表明,Softmax在生成质量和效率上均表现最优。
超参数khk_hkh的影响
本文将khk_hkh从5%调整至20%,实验结果见表2。发现kh=5%k_h=5\%kh=5%时,模型生成质量已接近标准注意力;且与kh=10%k_h=10\%kh=10%和kh=20%k_h=20\%kh=20%相比,kh=5%k_h=5\%kh=5%的计算量分别减少约一半和四分之三,在效率和质量之间实现了最优权衡。
6.5 可视化结果
图5和图7展示了Wan2.1-1.3B模型在SLA和各基线方法微调后的视频生成效果。结果表明,即使在95%的高稀疏度下,SLA生成的视频质量仍与标准注意力相当;而其他方法即使在低于90%的稀疏度下,生成的视频仍存在明显失真。


8 结论
本文提出一种可训练的稀疏-线性注意力机制(SLA),将稀疏注意力与线性注意力统一整合,实现扩散Transformer的加速。SLA根据注意力权重的重要性分配计算资源:对核心权重采用O(N2)O(N^2)O(N2)的标准注意力计算,对边缘权重采用O(N)O(N)O(N)的线性注意力计算,对可忽略权重直接跳过计算。该设计在保证模型效果的前提下,大幅降低了注意力机制的计算成本。
实验结果表明,仅通过少量微调步骤,SLA即可实现模型的高效加速:在Wan2.1-1.3B模型上,SLA将注意力计算量减少20倍,GPU核函数速度提升13.7倍,视频生成端到端速度提升2.2倍,且全程未降低视频生成质量。
附录
额外的效率优化策略
由于SLA的效率高度依赖稀疏模式,本文针对不同稀疏度设计了多种互补的优化策略,大幅提升了计算效率:
- 查找表优化 :当McM_cMc的稀疏度极高时(如>90%),逐行/列扫描掩码值会产生显著的内存开销。为此,本文对每行/列的非零位置进行预处理并存储在查找表中,计算时仅访问查找表,大幅减少内存通信量。
- 线性注意力预聚合 :尽管算法1第13行和算法2第14行仅需一次矩阵加法,但当McM_cMc中标签为0的元素较多时(如>90%),重复执行加法会产生较高开销。为此,本文预计算行/列和∑jhj\sum_j h_j∑jhj、∑jzj\sum_j z_j∑jzj,并扣除Mc[i,j]≠0M_c[i,j]≠0Mc[i,j]=0对应的项,将90%的加法操作替换为仅10%的减法操作。
- 四俄国人法 :当Mc[i,j]=0M_c[i,j]=0Mc[i,j]=0的分块数量适中时(如约50%),本文为算法1第13行和算法2第14行设计了高效实现方案,采用四俄国人法(Arlazarov等人,1970):将hjh_jhj和zjz_jzj按ggg个连续分块为一组,预计算每组内所有2g2^g2g种可能的子集和;前向传播时,任意ggg个分块的子集和均可通过一次查表得到,无需实时求和,理论上可将计算量降低1/g1/g1/g倍。