62.不同路径
题目
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 "Start" )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 "Finish" )。
问总共有多少条不同的路径?
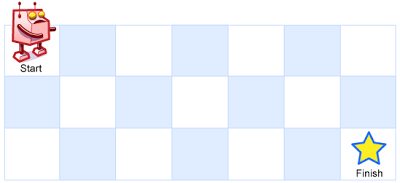
输入:m = 3, n = 7
输出:28思路
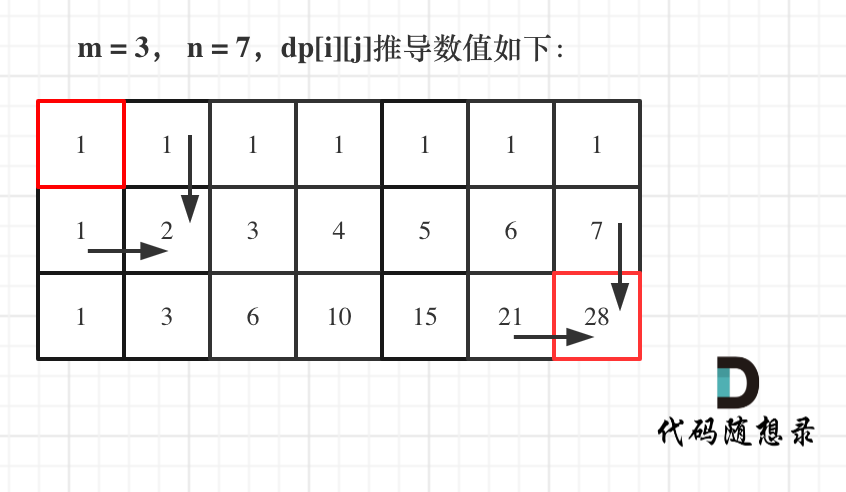
状态定义 :dp[i][j] 表示从起点到达 (i, j) 的路径数
状态转移 :找到转移方程很重要
机器人只能从上方 (i-1, j) 或左方 (i, j-1) 过来
所以:dp[i][j] = dp[i-1][j] + dp[i][j-1]表格中的每一个值都是斜对角的两个值相加
初始化:
-
第一行:只能一直向右走,
dp[0][j] = 1 -
第一列:只能一直向下走,
dp[i][0] = 1
代码
二维 DP 中,dp[i][j] 依赖:
-
正上方:
dp[i-1][j](上一行) -
正左方:
dp[i][j-1](当前行左边)
这时候可以发现,计算第 i 行时,只需要第 i-1 行的数据 ,更上面的行(i-2, i-3...)都没用了!
所以优化思想 用一个一维数组 dp[j],滚动更新 :当前行只依赖上一行 和当前行的前一个,可以用一维数组滚动更新。
-
更新前:
dp[j]存的是 上一行 第j列的值(dp[i-1][j]) -
更新后:
dp[j]存的是 当前行 第j列的值(dp[i][j])
java
class Solution{
public int uniquePaths(int m,int n){
// 只需要一行,dp[j] 表示当前行第j列的路径数
int[] dp = new int[n];
// 初始化第一行全为1
Arrays.fill(dp,1);
// 从第二行开始遍历
for(int i=1;i<m;i++){
// 第一列永远是1(只能从上面下来)
// 从第二列开始更新
for(int j=1;j<n;j++){
// dp[j] 还没更新,存的是上一行的值(即dp[i-1][j])
// dp[j-1] 已经更新,是当前行的值(即dp[i][j-1])
dp[j]=dp[j]+dp[j-1];
}
}
return dp[n-1];
}
}63. 不同路径 II
题目
给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角 (即 grid[0][0])。机器人尝试移动到 右下角 (即 grid[m - 1][n - 1])。机器人每次只能向下或者向右移动一步。
网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。
返回机器人能够到达右下角的不同路径数量。

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右思路
63. 不同路径 II 就是 62 的障碍物版本 ,核心区别在于遇到障碍物时路径数为 0 ,且初始化时需要处理障碍物阻断。
关键区别在于
1、初始化不同
62的初始化是第一行/列直接填 1。
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;而63题是遇到障碍物就停止,后面都是 0:
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;2、状态转移变化
62题的状态转移是:
dp[i][j] = dp[i-1][j] + dp[i][j-1];63题多了障碍物的判断,如果碰到障碍物那么这里填0:
if (obstacleGrid[i][j] == 1) {
dp[i][j] = 0; // 障碍物,不通
} else {
dp[i][j] = dp[i-1][j] + dp[i][j-1]; // 正常转移
}代码
java
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
// 起点或终点有障碍物,直接返回 0
if (obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1) return 0;
int[][] dp = new int[m][n];
dp[0][0] = 1; // 起点
// 第一列:遇到障碍物就停
for (int i = 1; i < m; i++) {
if (obstacleGrid[i][0] == 0) dp[i][0] = dp[i-1][0];
else dp[i][0] = 0;
}
// 第一行:遇到障碍物就停
for (int j = 1; j < n; j++) {
if (obstacleGrid[0][j] == 0) dp[0][j] = dp[0][j-1];
else dp[0][j] = 0;
}
// 填充其余,状态转移
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) dp[i][j] = 0;
else dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
}