LeetCode 算法：盛最多水的容器c++

原题链接🔗 ：盛最多水的容器
难度：中等⭐️⭐️

题目

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1 ：

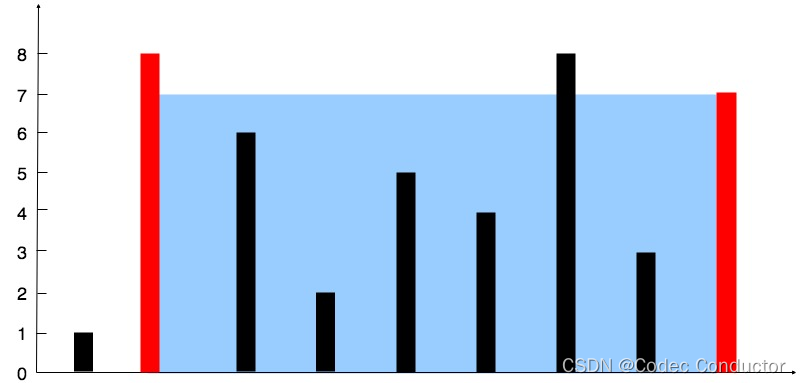
输入：[1,8,6,2,5,4,8,3,7]

输出：49

解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2 ：

输入：height = [1,1]

输出：1

提示：

n == height.length

2 <= n <= 10⁵

0 <= height[i] <= 10⁴

题解

双指针

题解：

LeetCode上的"盛最多水的容器"问题是一个典型的双指针问题，它要求你找到一个容器的形状，使得其盛水的体积最大。容器的形状由一个整数数组表示，其中每个元素代表容器在该位置的宽度。

这个问题可以通过以下逻辑来解决：

初始化指针：设置两个指针 left 和 right，分别指向数组的开始和结束位置。

计算面积 ：在每一步中，计算两个指针之间的面积。面积可以通过 min(height[left], height[right]) * (right - left) 来计算，其中 min(height[left], height[right]) 是两个指针中较小的高度，(right - left) 是两个指针之间的宽度。

更新最大面积：将当前面积与之前记录的最大面积进行比较，并更新最大面积。

移动指针 ：移动 left 或 right 指针以尝试找到更大的面积。选择移动哪个指针取决于 height[left] 和 height[right] 的值。如果 height[left] < height[right]，则移动 left 指针，因为移动较短的边可以更快地尝试新的高度。反之，则移动 right 指针。

循环结束条件：当 left 和 right 指针相遇时，循环结束。

返回结果：返回记录的最大面积。

这个算法的关键在于理解，移动较短边的指针可以更快地探索新的高度，因为容器的面积由两个因素决定：宽度和高度。当宽度固定时，高度越小，面积越小。因此，通过移动较短边的指针，我们可以更快地找到可能的更大面积。

复杂度：时间复杂度O(N)，空间复杂度O(1)。
代码过程:

初始化两个指针 left 和 right 分别指向数组的开始和结束位置。

在 while 循环中，计算当前面积 width *min(height[left], height[right])，其中 width 是两个指针之间的距离，min(height[left], height[right]) 是容器在当前指针位置的最小高度。

更新 max_area 为当前面积和已知最大面积之间的较大值。

移动较短边的指针，因为移动较长边的指针不会增加面积。

当两个指针相遇时，循环结束。

c++ demo:

cpp 复制代码

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int maxArea(vector<int>& height) {
    int max_area = 0;
    int left = 0;
    int right = height.size() - 1;

    while (left < right) {
        int width = right - left;
        int current_area = width * min(height[left], height[right]);
        max_area = max(max_area, current_area);

        if (height[left] < height[right]) {
            left++;
        }
        else {
            right--;
        }
    }

    return max_area;
}

int main() {
    // 示例输入
    vector<int> height1 = { 1,8,6,2,5,4,8,3,7 };
    vector<int> height2 = { 1,1,1 };

    // 调用 maxArea 函数并打印结果
    cout << "Maximum water that can be trapped with height1: " << maxArea(height1) << endl;
    cout << "Maximum water that can be trapped with height2: " << maxArea(height2) << endl;

    return 0;
}

输出结果：

Maximum water that can be trapped with height1: 49

Maximum water that can be trapped with height2: 2