基于广义极大极小凹惩罚的心电信号降噪方法（MATLAB R2021B）

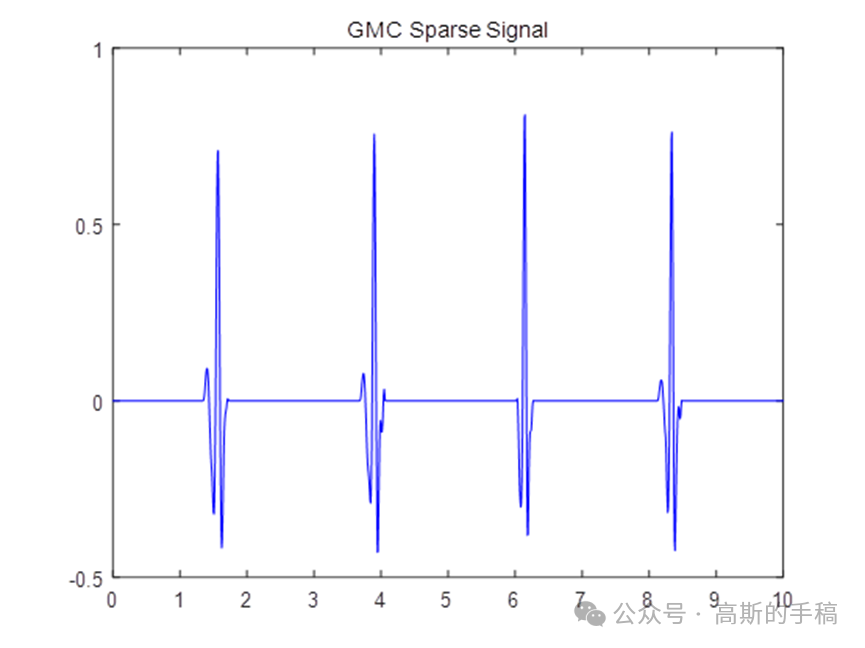
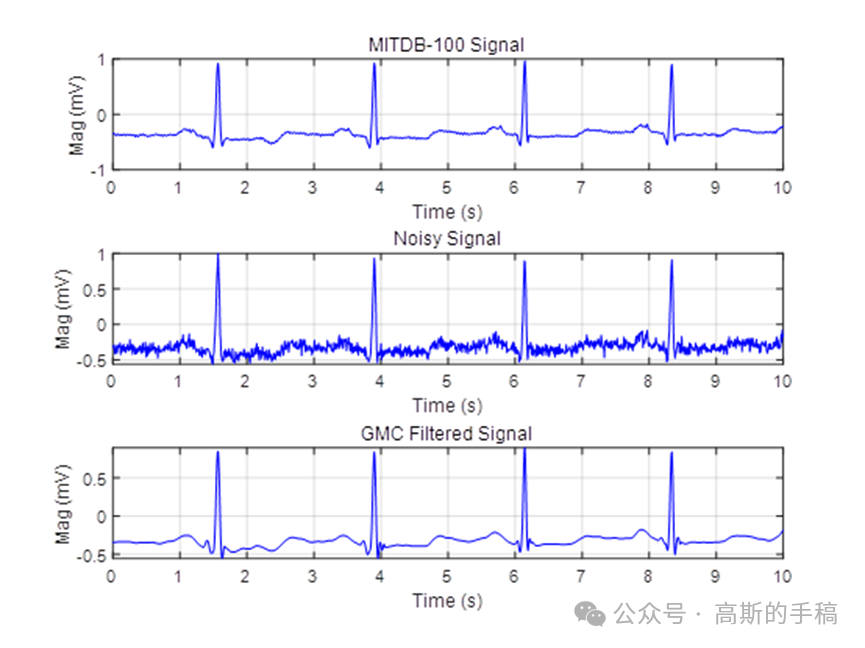
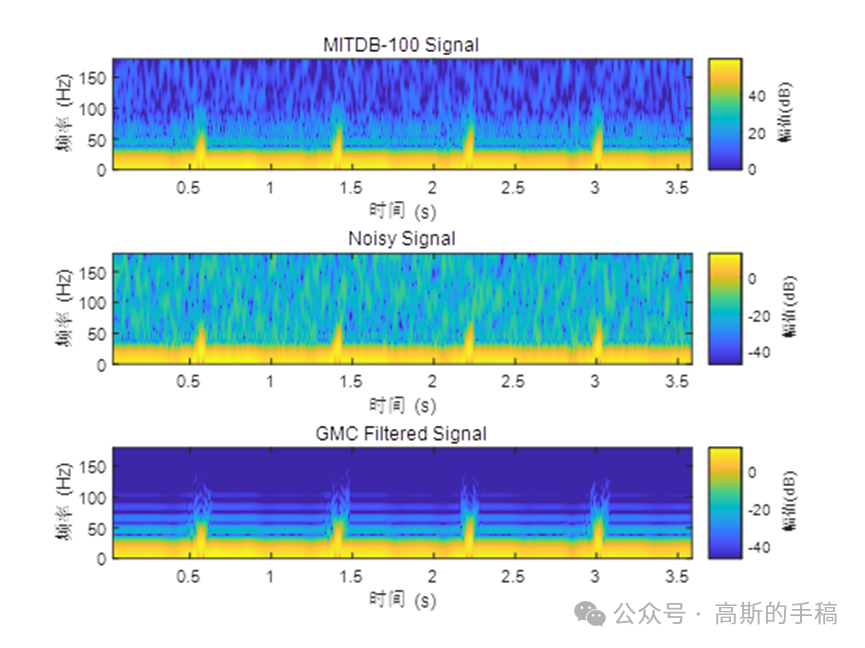
凸优化是数学最优化的一个子领域，研究定义于凸集中的凸函数最小化问题。由于心电信号降噪的过程可以理解为求信号的稀疏近似解，因此基于凸优化和稀疏性表达的去噪方法可用于心电信号处理。在凸优化的数学模型中，惩罚项的选取对最终结果会产生较大影响。1范数作为惩罚项是产生稀疏近似解的一个较为广泛的选择。在1范数的基础上，广义极大极小凹罚函数能够进一步提高解的稀疏性，大大提高降噪效果，而且还能够避免产生局部最小值，更容易使所得到的解达到全局最优。因此，采用基于GMC的凸优化方法对心电信号进行降噪处理，创新运行环境为MATLAB R2021B。

function 

% [x, v] = srls_GMC(y, A, AH, rho, lam, gamma)

% Saddle point problem:
%
% argmin_x  argmax_v { F(x,v) =
%  1/2 ||y - A x||^2 + lam ||x||_1 - gamma/2 ||A(x-v)||_2^2 - lam ||v||_1 }
%
% INPUT
%   y       data
%   A, AH   operators for A and A^H
%   rho     rho >= maximum eigenvalue of A^H A
%   lam     regularization parameter, lam > 0
%   gamma   0 <= gamma < 1
%
% OUTPUT
%   x, v

MAX_ITER = 10000;
TOL_STOP = 1e-4;

% soft thresholding for complex data
soft = @(x, T) max(1 - T./abs(x), 0) .* x;

% soft thresholding for real data
% soft = @(t, T) max(t - T, 0) + min(t + T, 0);

% rho = max(eig(A'*A));
mu = 1.9 / ( rho * max( 1,  gamma / (1-gamma) ) );

AHy = AH(y);

% initialization
x = zeros(size(AHy));
v = zeros(size(AHy));

iter = 0;
old_x = x;
delta_x = [inf];

while (delta_x(end) > TOL_STOP) && (iter < MAX_ITER)    
    iter = iter + 1;
    
    % update x
    zx = x - mu * ( AH(A(x + gamma*(v-x))) - AHy );
    zv = v - mu * ( gamma * AH(A(v-x)) );
    
    % update v
    x = soft(zx, mu * lam);
    v = soft(zv, mu * lam);
    
    delta_x(iter) = max(abs( x(:) - old_x(:) )) / max(abs(old_x(:)));
    old_x = x;    
    %完整代码：https://mbd.pub/o/bread/mbd-ZZaZmZZs

end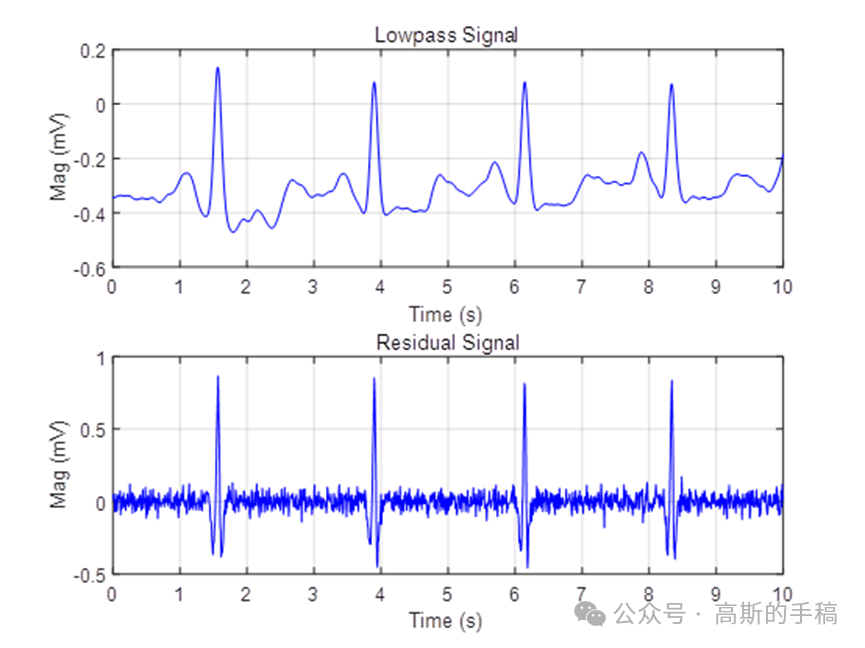

工学博士，担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家，擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。