【机器学习】朴素贝叶斯算法及其应用探索

🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈｜炫酷HTML | JavaScript基础

💫个人格言: "如无必要，勿增实体"

文章目录

朴素贝叶斯算法及其应用探索
- 引言
- [1. 朴素贝叶斯基本概念](#1. 朴素贝叶斯基本概念)
- - [1.1 贝叶斯定理回顾](#1.1 贝叶斯定理回顾)
  - [1.2 朴素贝叶斯模型概述](#1.2 朴素贝叶斯模型概述)
- [2. 数学推导](#2. 数学推导)
- - [2.1 多项式模型](#2.1 多项式模型)
  - [2.2 概率计算](#2.2 概率计算)
- [3. 朴素贝叶斯的优点](#3. 朴素贝叶斯的优点)
- [4. 缺点与局限性](#4. 缺点与局限性)
- [5. 应用案例](#5. 应用案例)
- - [5.1 文本分类](#5.1 文本分类)
  - [5.2 垃圾邮件过滤](#5.2 垃圾邮件过滤)
  - [5.3 医疗诊断](#5.3 医疗诊断)
- [6. 结语](#6. 结语)

朴素贝叶斯算法及其应用探索

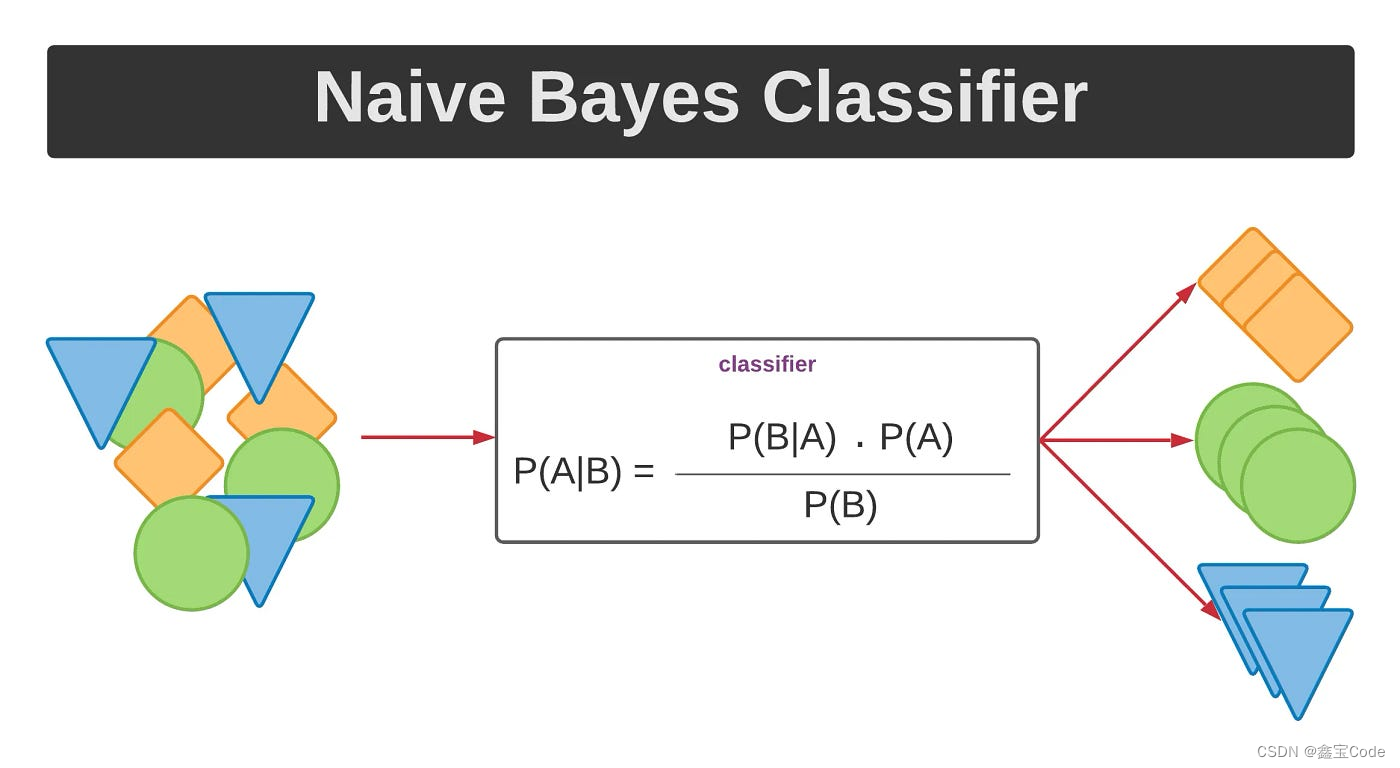
引言

在机器学习的广阔领域中，朴素贝叶斯分类器以其实现简单、计算高效和解释性强等特点，成为了一颗璀璨的明星。尽管名字中带有"朴素"二字，它在文本分类、垃圾邮件过滤、情感分析等多个领域展现出了不凡的效果。本文将深入浅出地介绍朴素贝叶斯的基本原理、数学推导、优缺点以及实际应用案例，旨在为读者构建一个全面而深刻的理解框架。

1. 朴素贝叶斯基本概念

1.1 贝叶斯定理回顾

一切始于贝叶斯定理，它是概率论中的一个核心公式，描述了两个条件概率之间的关系。给定事件A和B，贝叶斯定理表达为：

P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B) = \frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)

其中，(P(A|B))是在已知B发生的情况下A发生的概率，(P(B|A))是A发生时B发生的概率，(P(A))和(P(B))分别是A和B独立发生的概率。

1.2 朴素贝叶斯模型概述

朴素贝叶斯分类器基于贝叶斯定理，通过学习训练数据集中的特征与类别之间的概率关系来进行预测。其"朴素"之处在于假设特征之间相互独立，这一简化虽然在现实中很难严格成立，但却大大简化了计算复杂度，使得模型在很多情况下依然能够获得较好的性能。

2. 数学推导

2.1 多项式模型

对于离散特征，我们通常采用多项式模型。假设有一个文档分类问题，文档由词构成，每个词可以看作一个特征。设(c)为类别，(x_i)为第(i)个特征（词），则文档属于类别(c)的概率可以通过以下公式计算：

P ( c ∣ x 1 , x 2 , . . . , x n ) = P ( c ) P ( x 1 ∣ c ) P ( x 2 ∣ c ) . . . P ( x n ∣ c ) P ( x 1 , x 2 , . . . , x n ) P(c|x_1, x_2, ..., x_n) = \frac{P(c)P(x_1|c)P(x_2|c)...P(x_n|c)}{P(x_1, x_2, ..., x_n)} P(c∣x1,x2,...,xn)=P(x1,x2,...,xn)P(c)P(x1∣c)P(x2∣c)...P(xn∣c)

由于分母对于所有类别都是相同的，且不影响比较，因此可以省略。另外，根据朴素假设，上式可简化为：

P ( c ∣ x 1 , x 2 , . . . , x n ) ∝ P ( c ) ∏ i = 1 n P ( x i ∣ c ) P(c|x_1, x_2, ..., x_n) \propto P(c)\prod_{i=1}^{n}P(x_i|c) P(c∣x1,x2,...,xn)∝P(c)i=1∏nP(xi∣c)

2.2 概率计算

类先验概率 (P©)：是指训练集中类别©出现的概率。
条件概率 (P(x_i|c))：在类别(c)下，特征(x_i)出现的概率，通常需要平滑处理（如拉普拉斯修正）来避免概率为0的情况。

3. 朴素贝叶斯的优点

计算效率高：由于特征独立假设，使得计算复杂度大大降低，适合大规模数据集。
易于理解和实现：模型简单直观，不需要复杂的迭代过程。
对缺失数据不敏感：即使部分特征缺失，仍然可以根据其他特征进行预测。
具有较好的解释性：可以直观地看到各个特征对预测结果的影响。

4. 缺点与局限性

特征独立假设过于简化：在实际应用中，特征往往存在相关性，这会限制模型的表现。
估计概率时的小数问题：特别是对于稀有事件，可能因为缺乏足够的训练样本来准确估计概率。
分类边界问题：朴素贝叶斯直接依据概率进行分类，无法构造复杂的决策边界。

5. 应用案例

5.1 文本分类

朴素贝叶斯是文本分类领域的经典算法之一，常用于新闻分类、情感分析等任务。通过计算文档中各个词在不同类别下的条件概率，判断文档最可能属于哪个类别。

5.2 垃圾邮件过滤

通过学习垃圾邮件和非垃圾邮件中词汇的出现频率，朴素贝叶斯能有效识别并过滤掉垃圾邮件。它的高效性和易部署性使其成为许多邮件系统的首选技术。

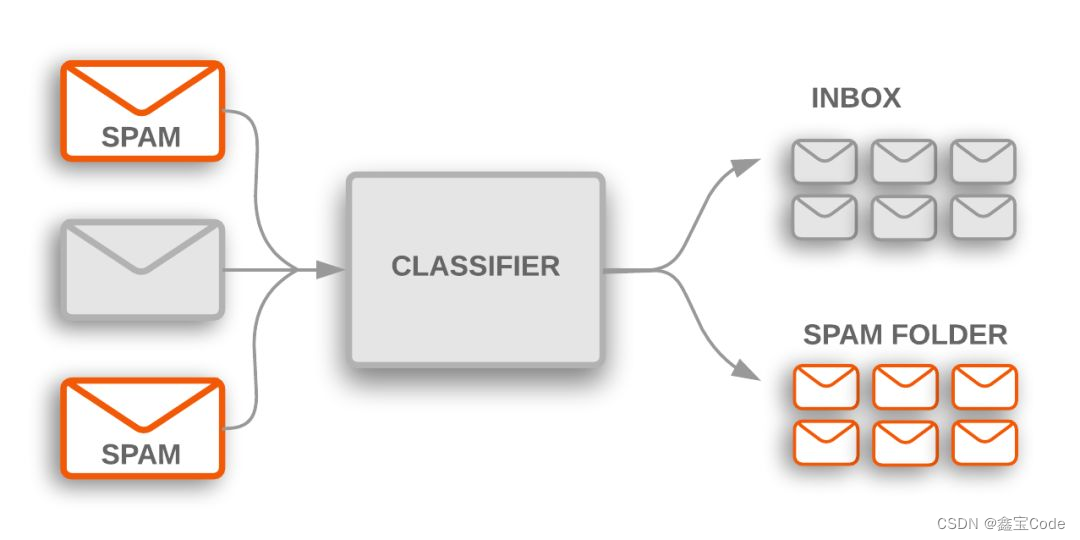
5.3 医疗诊断

在医疗领域，朴素贝叶斯被用来预测疾病的可能性，通过分析病人的各种症状（特征）与已知疾病之间的关联概率。

下面是一个简单的朴素贝叶斯分类器的Python实现示例，用于文本分类任务。这个例子使用了sklearn库中的MultinomialNB类，这是实现多项式朴素贝叶斯的一个常用工具，非常适合处理文本数据。

首先，确保你已经安装了scikit-learn库。如果未安装，可以通过pip安装：

python 复制代码

pip install scikit-learn

接下来是Python代码示例：

python 复制代码

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score

# 示例：使用Iris数据集进行分类（这里仅为了演示，实际上Iris更适合用非朴素贝叶斯方法）
# 但为了说明如何使用朴素贝叶斯，我们将数据转换为文本形式处理
iris = load_iris()
X, y = iris.data, iris.target

# 将数值数据转换为字符串，模拟文本分类任务
X_text = [' '.join(map(str, row)) for row in X]

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_text, y, test_size=0.2, random_state=42)

# 特征提取：将文本数据转换为词频矩阵
vectorizer = CountVectorizer()
X_train_transformed = vectorizer.fit_transform(X_train)
X_test_transformed = vectorizer.transform(X_test)

# 使用多项式朴素贝叶斯模型
clf = MultinomialNB()
clf.fit(X_train_transformed, y_train)

# 预测
y_pred = clf.predict(X_test_transformed)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy}")

# 注意：这个例子是为了演示朴素贝叶斯的使用，实际上Iris数据集并不适合朴素贝叶斯分类，
# 因为它是结构化的数值数据，而且特征之间存在相关性，朴素贝叶斯更适合处理特征独立的场景，如文本分类。

记住，上面的示例中使用Iris数据集是为了展示如何使用朴素贝叶斯模型，但实际上Iris数据集包含的是数值特征，并且特征之间存在相关性，因此并不是朴素贝叶斯算法的理想应用场景。朴素贝叶斯更常用于处理特征之间相互独立的问题，例如文本分类。

6. 结语

尽管朴素贝叶斯算法基于一系列简化的假设，但其在处理大量实际问题时所展现出的高效性和准确性证明了其价值。随着大数据时代的到来，朴素贝叶斯算法因其独特的优势，在众多领域内持续发挥着重要作用。未来，随着更多复杂技术和模型的融合，朴素贝叶斯算法的应用将会更加广泛和深入。通过不断优化和创新，我们可以期待它在更多领域带来新的突破和惊喜。