冒泡排序
冒泡排序想必大家并不陌生,其思想是利用双层循环,依次比较每个数,第一次比较前n个数,将最大的数排至最后,再比较前n-1个数,选出次大的数排至倒数第二,以此类推,将无序数组升序排列出来。
直接实现
cpp
void Swap(int* p1, int* p2)
{
int* tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
// 冒泡排序
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
//这里要注意j要小于n-i-1,因为比较的是a[j]与a[j+1],要防止数组越界
for (int j = 0; j < n - i - 1; j++)
{
if (a[j] > a[j + 1])
{
Swap(&a[j], &a[j + 1]);
}
}
}
}
插入排序
插入排序与冒泡排序正好相反,其是从左到右排至有序,冒泡则是从右至左排至有序。插入排序的思想是利用双层循环依次排出前 i+1 个数,让前 i+1 个数有序,让第 i+1 个数与前 i 个数比较,让其排为升序或降序,接着将 i++,继续排前 i 个数,直至循环结束。
具体过程如图所示(将每步拆解画出):


代码实现为
cpp
// 插入排序
void InsertSort(int* a, int n)
{
//防止数组越界
for (int i = 0; i < n - 1; i++)
{
int end = i;
//这里的a[end+1]要注意使用i下标要小于n-1,防止越界
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
//end+1位置的值已经被记录,这里可以直接覆盖
a[end + 1] = a[end];
end--;
}
//如果tmp>=a[end],就不需要比较,因为前面end个数为有序,a[end]位置为最大的值
else
{
break;
}
}
//最后把end+1原本位置的值放到合适的位置上
a[end + 1] = tmp;
}
}选择排序
选择排序的思想就是,每次遍历一遍数组,第一次遍历前n个数,找出最大数的坐标,与最后一个位置的数交换,或找出最小数的坐标,与第一个位置的数交换,然后遍历前n-1或后 n-1个数,找出次大或次小的数,进行交换,以此类推。
cpp
// 选择排序
void SelectSort(int* a, int n)
{
int end = n - 1;
while (end >= 0)
{
int maxi = 0;
//每次取第一个位置的地方作为最大值的坐标进行比较,
//所以,循环从1开始,不必与自己位置的值比较
for (int i = 1; i <= end; i++)
{
if (a[maxi] < a[i])
{
maxi = i;
}
}
Swap(&a[end], &a[maxi]);
end--;
}
}在此基础上,我们可以进行改进优化,每次取出最大值和最小值的坐标,然后与结尾和开头交换,再begin++、end--,缩小范围将继续找次小和次大的值。
但是优化的选择排序中就要注意一个小细节
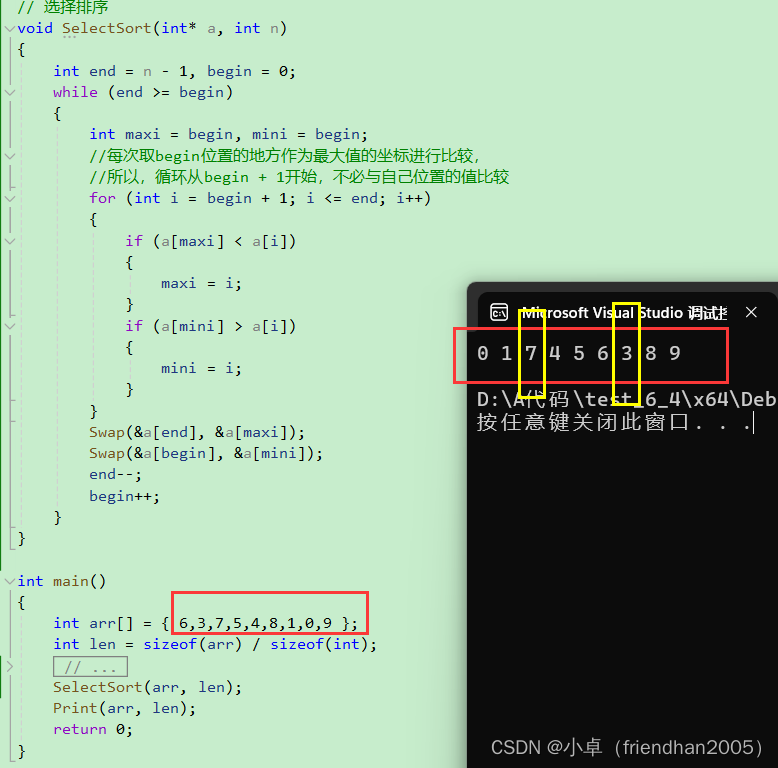
按照这个代码,似乎并没有很好的实现排序,但如果仔细观察,似乎是这两个位置反了导致的问题,那究竟为什么会出问题?我们画图来解释。
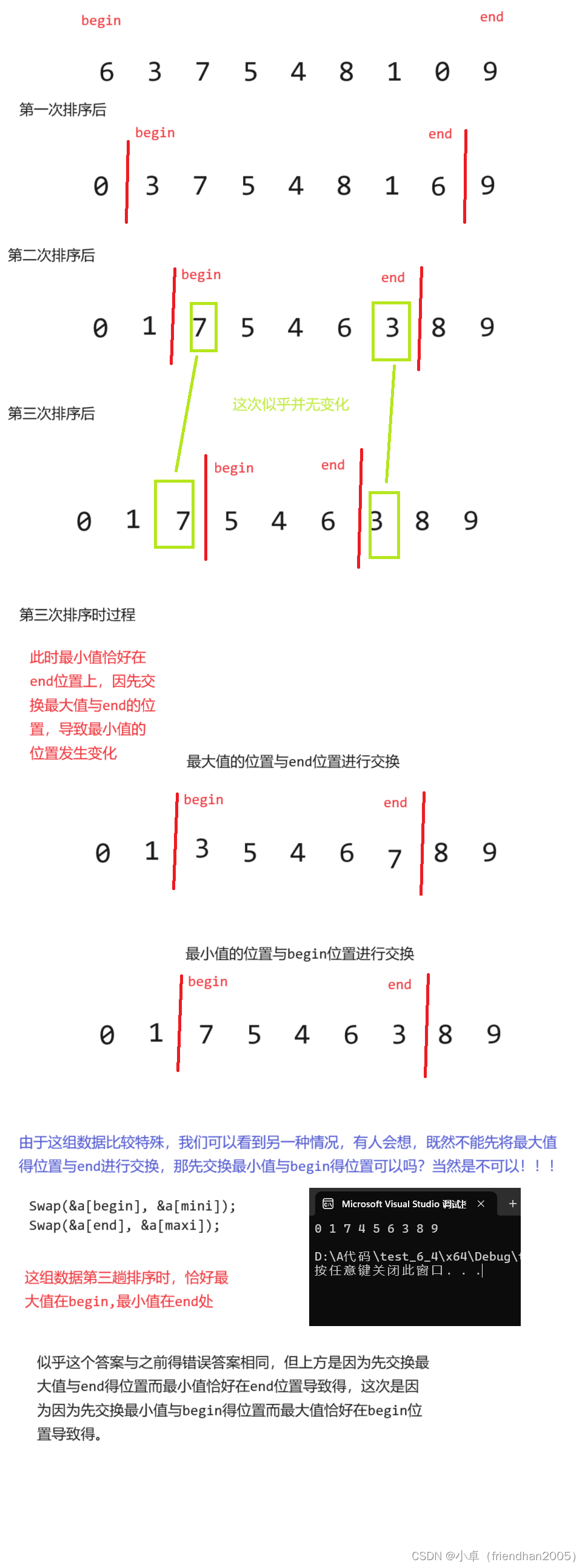
所以说,细节决定成败,下面是正确的优化后的选择排序代码。
cpp
// 选择排序
void SelectSort(int* a, int n)
{
int end = n - 1, begin = 0;
while (end >= begin)
{
int maxi = begin, mini = begin;
//每次取begin位置的地方作为最大值的坐标进行比较,
//所以,循环从begin + 1开始,不必与自己位置的值比较
for (int i = begin + 1; i <= end; i++)
{
if (a[maxi] < a[i])
{
maxi = i;
}
if (a[mini] > a[i])
{
mini = i;
}
}
Swap(&a[end], &a[maxi]);
//因为先交换最大值与end位置,要注意最小值在end位置的情况
//此时最小值被换到了记录maxi的位置
if (mini == end)
{
mini = maxi;
}
Swap(&a[begin], &a[mini]);
end--;
begin++;
}
}
cpp
// 选择排序
void SelectSort(int* a, int n)
{
int end = n - 1, begin = 0;
while (end >= begin)
{
int maxi = begin, mini = begin;
//每次取begin位置的地方作为最大值的坐标进行比较,
//所以,循环从begin + 1开始,不必与自己位置的值比较
for (int i = begin + 1; i <= end; i++)
{
if (a[maxi] < a[i])
{
maxi = i;
}
if (a[mini] > a[i])
{
mini = i;
}
}
Swap(&a[begin], &a[mini]);
//因为先交换最小值与begin位置,要注意最大值在begin位置的情况
//此时的最大值被换到记录mini的位置
if (maxi == begin)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
end--;
begin++;
}
}总结加三种排序算法的比较

我们可以通过一些办法来验证
这是利用C语言中的函数,随机生成100000个随机数,分别计算运行这三个排序算法所耗费的时间。
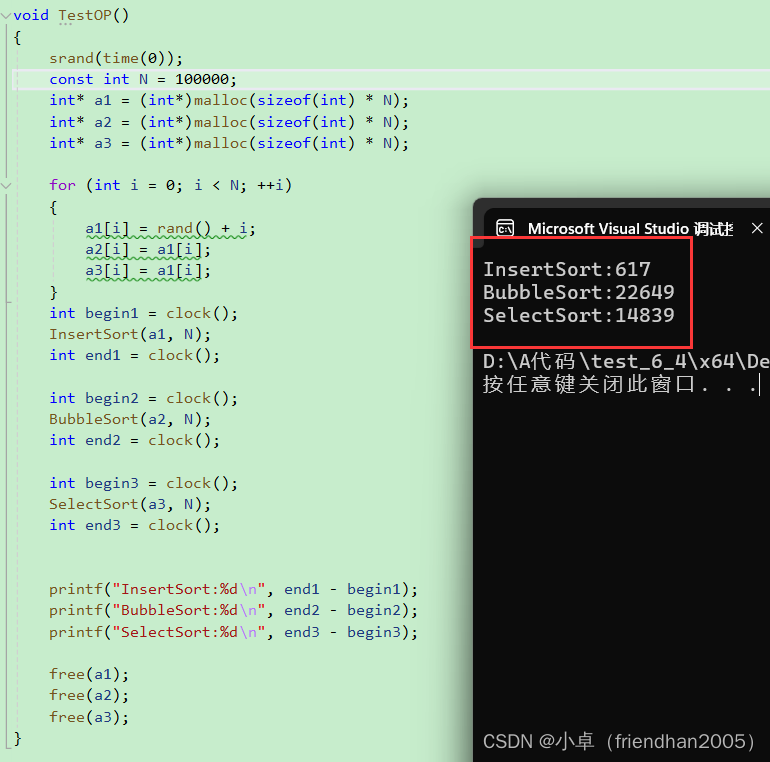
可以清楚的看到,插入排序比其他两个要好很多,插入排序的适应性非常强。
总的来说,插入排序是时间复杂度为O(N^2)的排序算法中最好的一个。希尔排序就是运用了插入排序改良实现的。