本章我们继续讲排序算法,这里我们将学习选择排序,也是一个很普遍很常见的排序算法,逻辑和代码都比较简单,比较容易掌握,我们直接走起
选择排序
基本思想:选择排序(SelectSort),即每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完
我们这里以排升序为例
选择排序与冒泡排序一样,也分为内层循环和外层循环,内层循环是找出最小的元素放到未排序数组的第一位,外层循环按照内层逻辑,一步一步的将元素由小到大依次放到数组内,完成排序
单趟逻辑 :单趟排序就是从记录本次循环的第一个元素,依次向后比较,若后面的元素大于记录的元素,那么就将记录的元素换为更小的元素,并记录此时记录元素的下标 ,方便在出循环后进行交换,找到数组末尾,本次单趟循环结束,此时记录的元素就是最小元素,那么我们就进行交换
**整体逻辑:**沿用单趟逻辑,多次进行排序,若有n个数据,那么就需要外层循环n-1次,将数据全部排好。
逻辑图
代码实现
void SelectSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
int tmp = a[i];
int k = i;
for (int j = i + 1; j < n; j++)
{
if (a[j] < tmp)
{
tmp = a[j];
k = j;
}
}
Swap(&a[i], &a[k]);
}
}优化
思路:上面的选择排序是基本的选择排序,我们可以发现,他每次循环都需要遍历未排序的数组去寻找最小的元素,那么我们换一种思路,如果我们在遍历未排序的数组时,同时找到最大的元素和最小的元素,是不是就减少了一半的循环量,思路有了,我们就直接开始实现
总体的思路还是和上面大差不差,但是这次我们需要多建一个变量end,来记录数组末尾的位置
然后依次进行遍历,之前我们用tmp记录最小的数,这里就需要用两个变量max 和 min来分别记录最大值和最小值,为了方便我们直接记录下标,这样就不用新建变量来记录下标了,而且还可以直接进行比较
流程图

优化代码(有瑕疵)
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int min = begin;
int max = begin;
for (int i = begin + 1; i <= end; i++)
{
if (a[i] > a[max])
{
max = i;
}
if (a[i] < a[min])
{
min = i;
}
}
Swap(&a[begin], &a[min]);
Swap(&a[end], &a[max]);
begin++;
end--;
}
}看了上面的分析和代码的实现,也许你会认为,这样就完成选择排序的优化,但是事实真的如此吗,先说结论,这个排序逻辑确实是这样的,代码基本也是对的,可以完成大多数的排序,但是有个别情况,是无法进行正确排序的,因此上面实现的是有瑕疵的
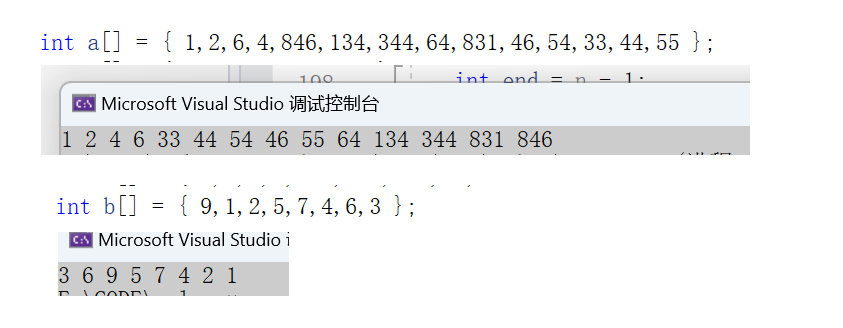
我们来分析一下,当第一轮排序时,我们上面的代码会记录
max为0,min为 1 ,begin为0,end为7
进行交换的时候,先交换begin和min
结果为 1 9 2 5 7 4 6 3
再交换max和end的时候
结果为 3 9 2 5 7 4 6 1
很显然,已经出错了,max在和end进行交换的时候,max已经变换了位置,因此我们找到了问题,找到了问题之后,我们就需要解决问题
我们只需要加一个判断条件,当最大值为begin时,第一步begin和min交换就会把max的值交换走,这时我们需要进行判断,如果begin==max,那么就将max的值赋为min,即此时最大值被交换到的位置,再进行第二步交换即可。
优化代码最终实现
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin + 1; i <= end; ++i)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
Swap(&a[begin], &a[mini]);
if (begin == maxi)
maxi = mini;
Swap(&a[end], &a[maxi]);
++begin;
--end;
}
}总结(冒泡排序和选择排序的区别)
冒泡排序的时间复杂度为O(n^2),其中n是要排序的元素数量。这是因为冒泡排序需要进行多次遍历,每次遍历都需要比较和交换元素。因此,对于大规模数据的排序,冒泡排序可能不是最有效的选择。
选择排序的时间复杂度也是O(n^2),但它的性能通常优于冒泡排序。因为选择排序只需要进行一次遍历,并且只需要进行一次比较和交换操作。因此,在处理大规模数据时,选择排序通常更为高效。
但如果遇到已经排好序的数据,冒泡排序只需要循环一次就能发现,并终止,但选择排序却需要继续遍历数组,在这一点上选择排序的效率是不如冒泡排序的。
