介绍
排序算法 是计算机科学中被广泛研究的一个课题。历时多年,它发展出了数十种算法,这些
算法都着眼于一个问题:如何将一个无序的数字数组整理成升序?先来学习一些"简单排序",它们很好懂,但效率不如其他排序算法。主打一个循序渐进👏
冒泡排序🐳
假设要对[4, 2, 7, 1, 3]进行排序。它现在是无序的,我们的目标是产生一个包含相同元素、升序的数组。
第 1 步:首先,比较 4 和 2。如图可见它们的顺序是错的

第 2 步:交换它们的位置
第 3 步:比较 4 和 7:

依次类推,每一次轮回过后,未排序的值中最大的那个都会"冒"到正确的位置上。
用python实现
python
def bubble_sort(list):
unsorted_until_index = len(list) - 1
sorted = False
while not sorted:
sorted = True
for i in range(unsorted_until_index):
if list[i] > list[i+1]:
sorted = False
list[i], list[i+1] = list[i+1], list[i]
unsorted_until_index = unsorted_until_index - 1
list = [65, 55, 45, 35, 25, 15, 10]
bubble_sort(list)
print(list)输出:
10, 15, 25, 35, 45, 55, 65
效率
冒泡排序的执行步骤可分为两种。
- 比较:比较两个数看哪个更大。
- 交换:交换两个数的位置以使它们按顺序排列
如果数组不只是随机打乱,而是完全反序,在这种最坏的情况下,每次比较过后都得进行一
次交换。
现在把两种步骤放在一起来看。一个含有 10 个元素的数组,需要:
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 次比较,以及 45 次交换,共 90 步。
效率太低了😓。元素量呈倍数增长,步数却呈指数增长,如下表所示:

因此描述冒泡排序效率的大 O 记法,是 O(N 2)。
规范一些来说:用 O(N 2)算法处理 N 个元素,大约需要 N 2步。
O(N 2)算法是比较低效的,随着数据量变多,其步数也剧增,如下图所示:
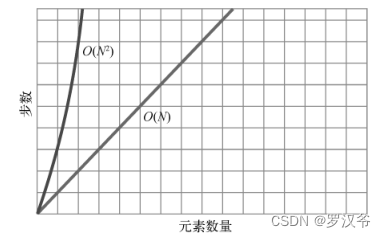
- 嵌套循环
js
function hasDuplicateValue(array) {
var steps = 0;
for (var i = 0; i < array.length; i++) {
for (var j = 0; j < array.length; j++) {
steps++;
if (i !== j && array[i] == array[j]) {
return true;
}
}
}
console.log(steps);
return false;
}
hasDuplicateValue([1,2,3])嵌套循环算法的效率就是 O(N^2)。一旦看到嵌套循环,你就应该马上想到 O(N2)
改进
以下时间复杂度:其大 O 记法是 O(N)
js
function hasDup(array){
var steps = 0;
var existsNumbers = [];
for (let i = 0; i < array.length; i++) {
steps++;
if(existsNumbers[array[i]]===undefined){
existsNumbers[array[i]] = 1;
}else{
return true;
}
}
console.log(steps);
return false;
}执行 hasDuplicateValue([1,2,3])的话,你会看到输出为 3,跟元素个数一致。
选择排序👈
冒泡排序算法,其效率是 O(N 2)。现在我们再来探索另一种排序算法,选择排序:
步骤
(1) 从左至右检查数组的每个格子,找出值最小的那个。在此过程中,我们会用一个变量来记住检查过的数字的最小值(事实上记住的是索引,但为了看起来方便,下图就直接写出数值)。
如果一个格子中的数字比记录的最小值还要小,就把变量改成该格子的索引。

(2) 知道哪个格子的值最小之后,将该格与本次检查的起点交换。第 1 次检查的起点是索引 0,第2此起点时索引1

(3) 重复第(1) (2)步,直至数组排好序
效率
选择排序的步骤可分为两类:比较和交换,也就是在每轮检查中把未排序的值跟该轮已遇到的最小值做比较,以及将最小值与该轮起点的值交换以使其位置正确。
但每轮的交换最多只有 1 次。如果该轮的最小值已在正确位置,就无须交换,否则要做 1 次交换。相比之下,冒泡排序在最坏情况(完全逆序)时,每次比较过后都要进行 1 次交换。

选择排序的大 O 记法为 O(N2),跟冒泡排序一样!🙋
因为:大 O 记法不包含一般数字,除非是指数。
例如:当数据量少于某个值时,O(N2)是比 O(100N)要快的,但过了这个值之后,O(100N)便反超 O(N 2),并一直保持优势!
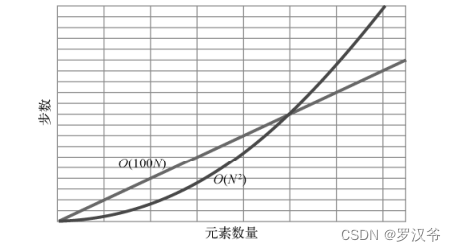
这就是大 O 记法忽略常数的原因。大 O 记法只表明,对于不同分类,存在一临界点,在这
一点之后,一类算法会快于另一类,并永远保持下去。至于这个点在哪里,大 O 并不关心。
插入排序✍
我们已经学过两种排序算法:冒泡排序和选择排序。虽然它们的效率都是 O(N 2),但其实选择排序比冒泡排序快一倍。现在来学第三种排序算法------插入排序。
在最坏的情况里,插入排序的时间复杂度跟冒泡排序、选择排序一样,都是 O(N2)
效率
插入排序包含 4 种步骤:移除、比较、平移和插入。要分析插入算法的效率,就得把每种步骤都统计一遍。
在数组完全逆序的最坏情况下,我们每一轮都要将 temp_value 左侧的所有值与temp_value 比较。因为那些值全都大于 temp_value,所以每一轮都要等到空隙移到最左端才能结束。
在第一轮,temp_value 为索引 1 的值,由于 temp_value 左侧只有一个值,所以最多进行一次比较。到了第二轮,最多进行两次比较,以此类推。到最后一轮时,就要拿 temp_value 以外的所有值与其进行比较。换言之,如果数组有 N 个元素,则最后一轮中最多进行 N - 1 次比较。

快速排序
快速排序真的很快。尽管在最坏情况(数组逆序)下它跟插入排序、选择排序的效率差不多,但在日常多见的平均情况中,它的确表现优异。
快速排序依赖于一个名为分区的概念,所以我们先从它开始了解。
步骤
(1) 把数组分区。使轴到正确的位置上去。
(2) 对轴左右的两个子数组递归地重复第 1、2 步,也就是说,两个子数组都各自分区,并形成各自的轴以及由轴分隔的更小的子数组。然后也对这些子数组分区,以此类推。
(3) 当分出的子数组长度为 0 或 1 时,即达到基准情形,无须进一步操作。

python实现
python
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quick_sort(left) + middle + quick_sort(right)
# 测试快速排序函数
arr = [3, 6, 8, 10, 1, 2, 1]
sorted_arr = quick_sort(arr)
print("排序后的数组:", sorted_arr)总结
懂得区分最好、平均、最坏情况,是为当前场景选择最优算法以及给现有算法调优以适应环境变化的关键。记住,虽然为最坏情况做好准备十分重要,但大部分时间我们面对的是平均情况。