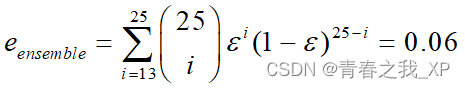目录
常见的有装袋(Bagging)和提升(Boosting)两种方法
[方法1 :装袋(Bagging)](#方法1 :装袋(Bagging))
[方法2 :提升(Boosting)](#方法2 :提升(Boosting))
[(三) 为什么要随机抽样训练集?](#(三) 为什么要随机抽样训练集?)
五、Adaboosting (Boosting集成方法的一种)
(一)基本思想基本思想)
本文将探讨集成学习方法的核心概念,包括其基本原理和两种主流技术:装袋(Bagging)与提升(Boosting)。我们将深入了解随机森林------一种基于Bagging的集成方法,并讨论其背后的思想、树的生成过程以及抽样策略。同时,我们也将介绍Adaboost算法的基本思想和工作原理,并通过实例加以说明。通过这篇文章,读者可以获得对集成分类器构建方法的全面了解,并掌握如何在Python中实现随机森林。
一、集成方法的一般思想
聚集多个分类器的预测来提高分类准确率,这种技术称为组合(ensemble)或分类器组合(classifier combination)方法,也就是集成方法
由训练数据构建一组基分类器,然后通过对每个基分类器的预测进行投票来进行分类。

二、集成方法的基本原理
假定有 25 基分类器:
-- 每个基分类器的误差均为 e = 0.35
-- 假定基分类器是独立的
-- 通过对这些基分类器的预测进行多数表决方法预测类标号
-- 仅当超过一半的基分类器都预测错误时,组合分类器才会做出错误的预测,此时误差率为:
远远低于基分类器的误差率。
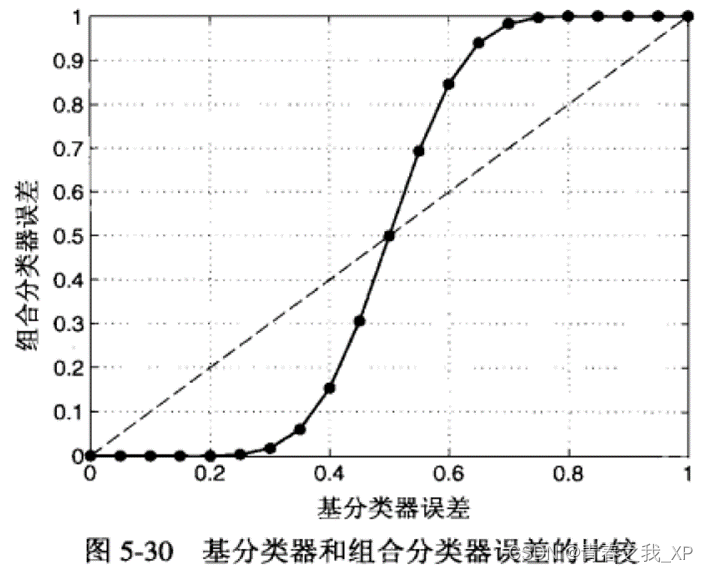
下图显示对于不同的基分类器误差率 e 下的 25 个二元分类器的组合分类器误差率 。
对角虚线表示所有基分类器都是等同的情况
实线表示所有基分类器独立时的情况
e > 0.5 时,组合分类器的性能不如基分类器
三、构建集成分类器的方法
基本思想:
在原始数据上构建多个分类器,然后在分类未知样本时聚集它们的预测结果。
常见的有装袋(Bagging)和提升(Boosting)两种方法
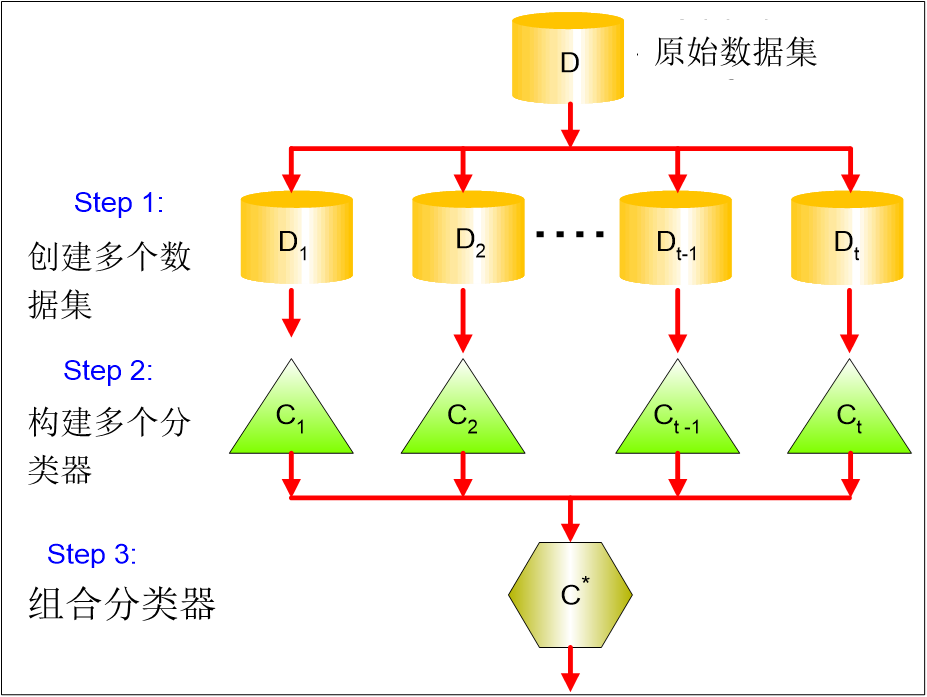
方法1 :装袋(Bagging)
Bagging原理如下图:
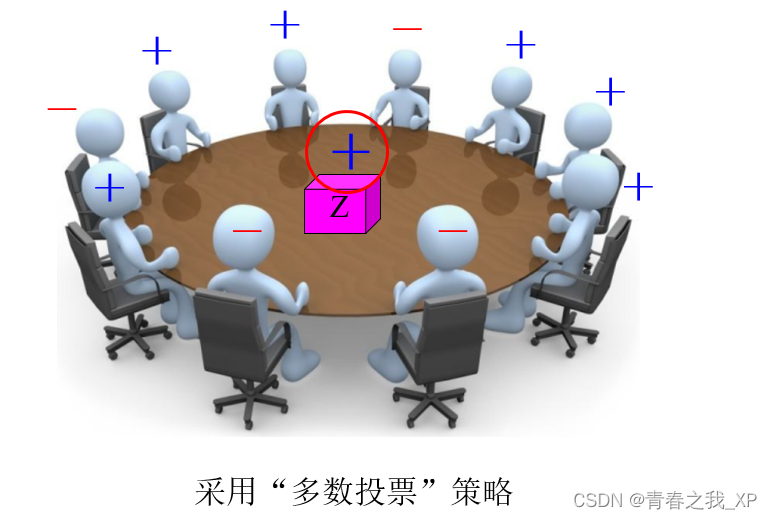
对于未知样本Z,预测Z的类标号
方法2 :提升(Boosting)
Boosting 方法是一种用来提高 弱分类算法 准确度的方法。
通过构造一个预测 函数 系列 , 然后以一定的方式将他们组合成一个预测函数。
Boosting 是一种提高任意给定学习算法准确度的方法。
Boosting 方法是一种针对提高弱分类算法准确度的有效技术。该方法的核心思想是通过构建一系列的预测函数,并将它们以特定的方式组合起来,从而形成一个更为强大和精准的预测模型。具体而言,Boosting 通过以下步骤来提升任意给定学习算法的准确度:
初始化:首先选择一个弱分类器作为基础模型,并确定一个权重分配方案,初始时通常所有数据点的权重相等。
迭代训练:在每一轮迭代中,根据上一次迭代中分类错误的样本调整权重,使得错误分类的样本在下一轮迭代中得到更多的关注。然后,使用调整后的权重训练新的弱分类器。
组合预测:将每个弱分类器的预测结果按照一定的权重进行组合,通常是加权投票或加权平均,以形成最终的预测函数。这个组合过程能够有效提升整体模型的准确度。
Boosting 方法的特点在于:
- 逐步增强:通过迭代的方式逐步增强模型的预测能力,每一步都试图修正上一步的错误。
- 权重调整:动态调整样本权重,使得模型在后续的学习过程中更加关注那些难以分类的样本。
- 模型组合:将多个弱分类器智能组合,形成一个强大的分类器,通常比单个分类器具有更高的准确度和鲁棒性。
总之,Boosting 是一种通用且强大的机器学习算法增强技术,它能够显著提升弱分类算法的性能,使其在许多实际问题中达到或接近最优的分类效果。
其核心思想是" 三个臭皮匠,顶过诸葛亮 "。
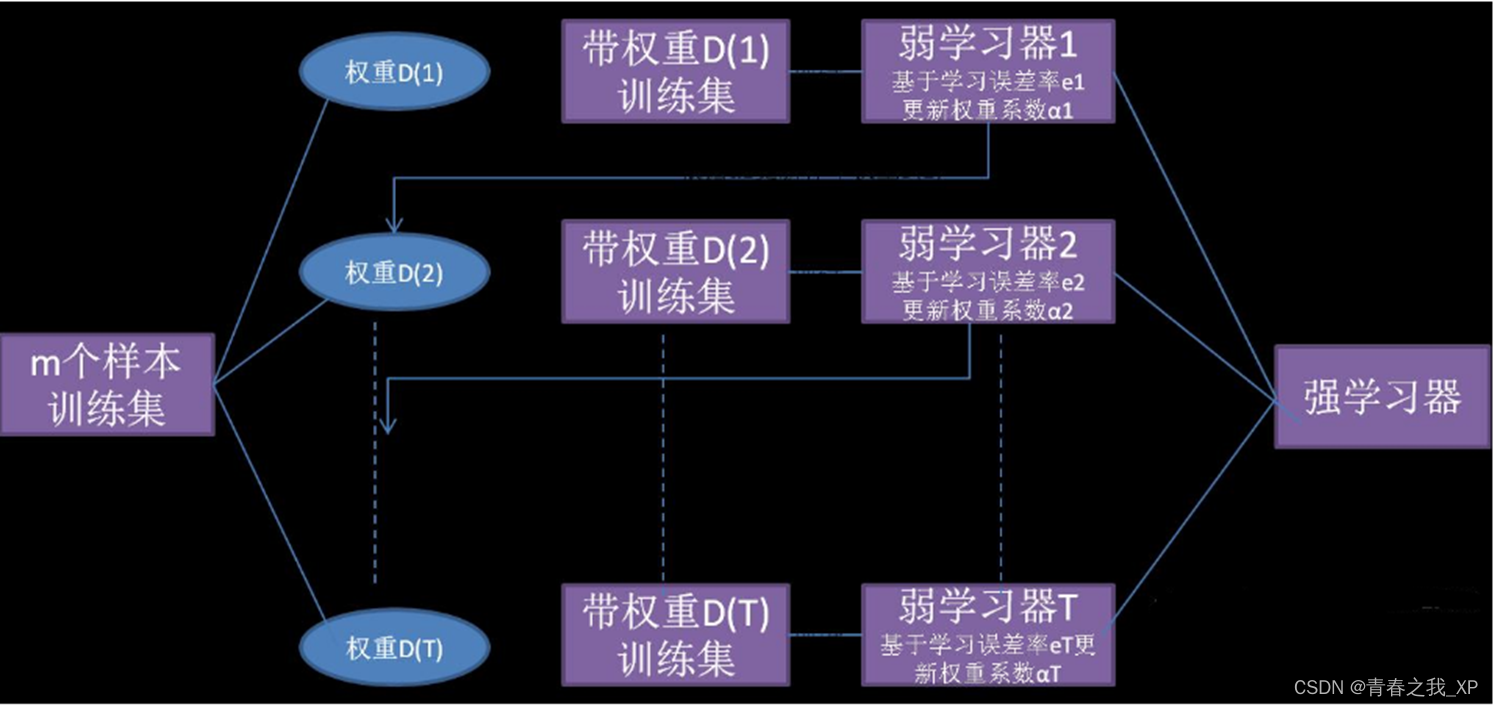
Boosting工作原理
• 首先从训练集用初始权重训练出一个弱学习器 1 ,根据弱学习器 1 的 学习误差率表现 来 更新 训练样本的权重,使得之前弱学习器 1 学习误差率高的训练样本点的权重变高,使得这些误差率高的点在后面的弱学习器 2 中得到更多的重视。
• 然后基于调整权重后的训练集来训练弱学习器 2. ,如此重复进行,直到弱学习器数达到事先指定的数目 T 。
• 最终将这 T 个弱学习器通过集合策略进行整合,得到最终的强学习器。


目前已有几个Boosting算法,其区别在于:
(1)每轮Boosting结束时如何更新训练样本的权值;
(2)如何组合每个分类器的预测。
四、随机森林(Bagging集成方法的一种)
随机森林就是通过集成学习的思想将多棵树集成的一种算法,它的基本单元是决策树,而它的本质属于机器学习的一大分支------集成学习方法。
随机森林的名称中有两个关键词,一个是"随机",一个就是"森林"。
"森林"很好理解,一棵叫做树,那么成百上千棵就可以叫做森林了,其实这也是随机森林的主要思想--集成思想的体现。"随机"的包括随机选取训练样本集和随机选取分裂属性集。
从直观角度来解释,每棵决策树都是一个分类器(假设现在针对的是分类问题),那么对于一个输入样本,N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果,将投票次数最多的类别指定为最终的输出。(一)随机森林bagging的思想:
将若干个弱分类器的分类结果进行投票选择,从而组成一个强分类器。
(二)随机森林中的每棵树是怎么生成的呢?
一开始提到的随机森林中的"随机"就是指的步骤a和步骤b中的两个随机性。两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入,使得随机森林不容易陷入过拟合,并且具有很好得抗噪能力(比如:对缺省值不敏感) 。(三) 为什么要随机抽样训练集?
如果不进行随机抽样,每棵树的训练集都一样,那么最终训练出的树分类结果也是完全一样的,这样的话完全没有集成的必要
(四)为什么要有放回地抽样?
如果不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有交集的,这样每棵树都是"有偏的"或"片面的",也就是说每棵树训练出来都是有很大的差异的;
而随机森林最后分类取决于多棵树(弱分类器)的投票表决,这种表决应该是"求同",因此使用完全不同的训练集来训练每棵树这样对最终分类结果是没有帮助的。
随机森林Python实现
请看下方链接
【机器学习系列】掌握随机森林:从基础原理到参数优化的全面指南_随机森林算法参数解释及调优-CSDN博客
五、Adaboosting (Boosting集成方法的一种)
(一)基本思想

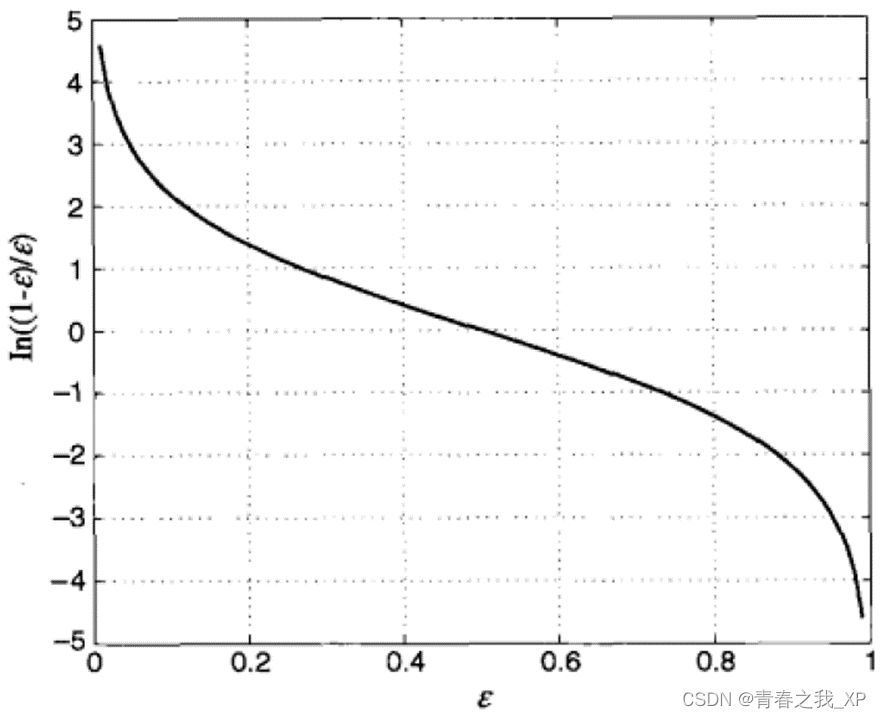
如果错误率e**i 接近0,则 α**i 有一个很大的正值。
如果错误率e**i 接近1,则 α**i 有一个很大的负值。

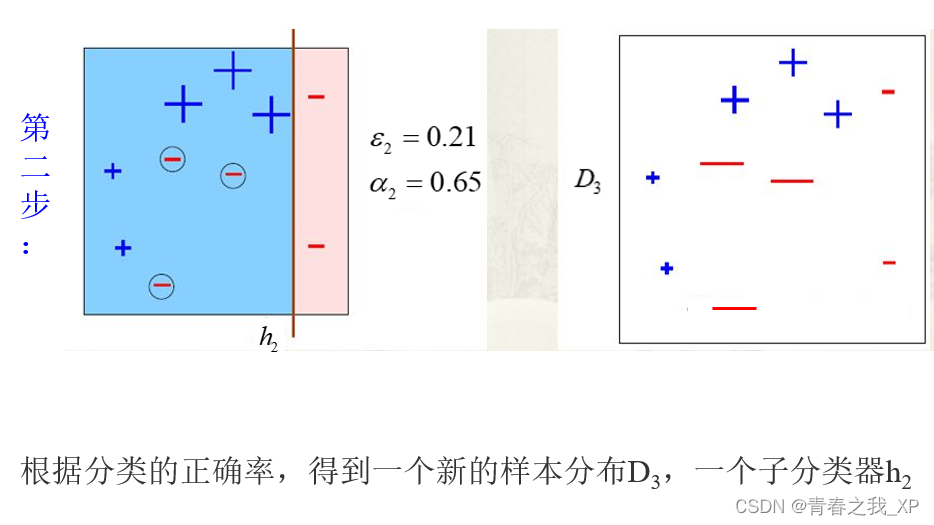
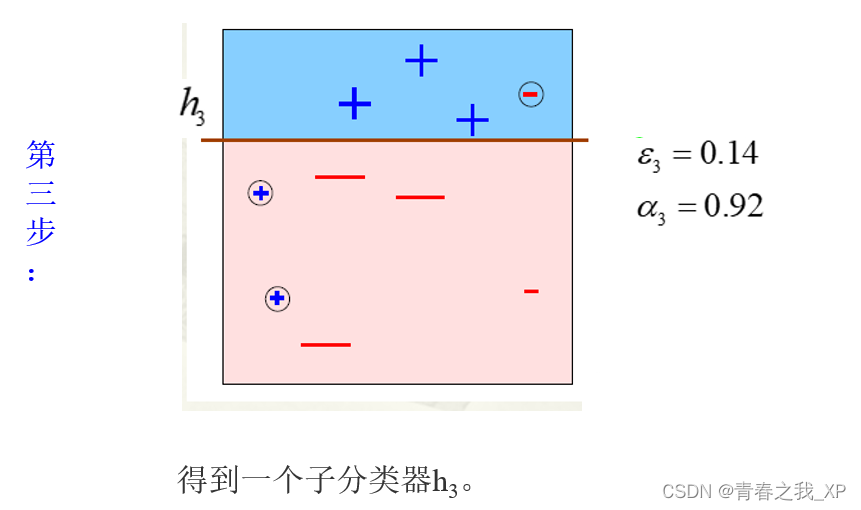
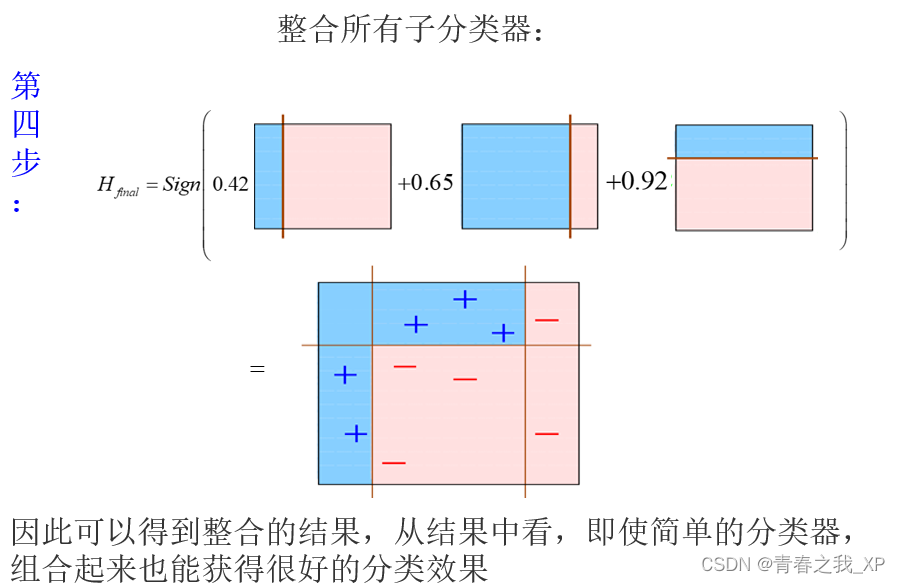
(二)Adaboosting举例说明