文章目录
- [1. 前言](#1. 前言)
- [2. 题目和分析](#2. 题目和分析)
-
- [2.1 代码实现](#2.1 代码实现)
- [2.2 反思 (重点)](#2.2 反思 (重点))
- 3.题目二(变式)
-
- [3.1 分析](#3.1 分析)
- [3.2 代码实现](#3.2 代码实现)
- [4. 题目三(变式)](#4. 题目三(变式))
-
- [4.1 分析](#4.1 分析)
- [4.2 代码实现](#4.2 代码实现)
1. 前言
相信大家看到青蛙跳台阶问题时,第一时间就会想到递归。那你知道为什么会使用递归吗?如果你对此一知半解的话,那么请跟随我的脚步,一起探索递归解决问题背后的秘密。
可能也有的读者会问,我不是学C语言的,看这个会不会不合适。对此,我只想说:编程的尽头是天马行空的脑洞和转化问题的能力,编程语言只是我们解决问题的工具,只要问题被解决了,用什么语言效果都是大差不差的。
那么,话不多说,Let's go!!!
2. 题目和分析
题目一:一只青蛙一次可以跳上一级台阶,也可以跳上二级台阶,求该青蛙跳上一个n级的台阶总共需要多少种跳法。
问题的描述很简单,那我们的破题关键在哪里呢?
我们可以先罗列几种情况,看一下有什么规律。
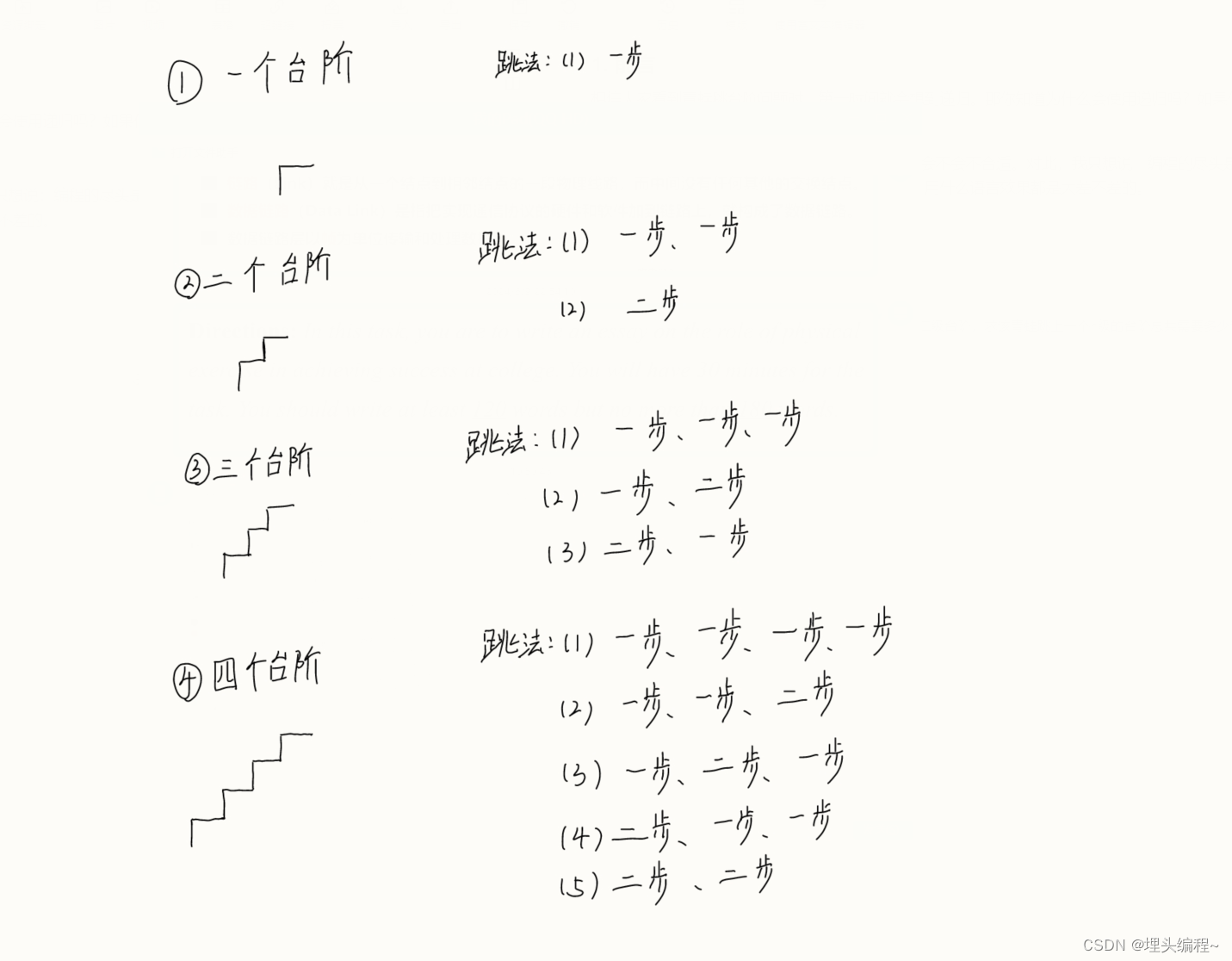
从这里,你可以发现一个规律:
当只有一个台阶时,青蛙它别无选择,它只需要跳一步就可以了;
当存在两个台阶时,青蛙此时就会有两种方法。第一种就是,当青蛙选择一开始先跳一步时,那么两个台阶就只剩下一个台阶要跳了,那还能怎么办,继续跳就完事了。
第二种就是,青蛙选择一次跳两步,两个台阶就被跳完了。
当存在三个台阶时,青蛙此时就会有三种方法。第一种:一步一步地跳。
第二种:先选择跳一步之后 ,再一次跳两步。
第三种:先选择跳两步,最后再跳一步就行。
后面的列举是一样的思路,限于篇幅的原因,这里就不再过多列举了。
看到这里,我们不妨假设,变量n为青蛙要跳的台阶数,函数Fun为计算青蛙台阶的方法个数。
c
int Fun(int n)
{
... //代填写的内容
}那么根据题目的要求,我们可以知道一个点,就是:Fun(1) = 1,Fun(2) = 2
仔细观察,我们可以发现一个规律:当台阶数n=3时,Fun(3) = Fun(2) + Fun(1)
...
为此,我们可以总结出一个递推公式,就是Fun(n) = Fun(n-1) + Fun(n-2) (n>2)。
为此,我们就可以开始写函数了。
2.1 代码实现
c
#include<stdio.h>
int Fun(int n)
{
if (n<=2) //递归退出条件
{
return n;
}
else
{
return Fun(n - 1) + Fun(n - 2);
}
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fun(n);
printf("%d\n", ret);
return 0;
}2.2 反思 (重点)
可能有的读者对这个规律总结的出现,仍然感觉到很诧异。那么我现在就用语言来解释这个递推公式背后的秘密。
我们可以想象一下,当台阶数大于2时:
当台阶数n=3时,聪明的青蛙此时就会说:"那我先跳1个台阶试试看后面的情况。" 既然青蛙已经跳过了1个台阶,那么总的台阶数就还剩2个。而这个问题不就又转换为:跳两个台阶有多少种跳法。
那这里可能有的读者还会提一个问题,如果青蛙先跳2个台阶呢?还会上述的推理过程吗?
其实大致的方向是不变的,就改一下顺序就可以了。为此你就可以理解Fun(n) = Fun(n-1) + Fun(n-2)这个公式的强大之处,它无关你跳的前后顺序。
看到这里,你可能还是不理解上述的语言表述,我就在多举一个例子
那么,当台阶数n=4,又会发生什么情况呢?Fun(4)
一样的解题思路:
当青蛙选择跳1步时,那么台阶就还剩3个,问题不就又转化为:求3个台阶有多少种跳法。Fun(3)
可是这样还不够啊,青蛙也有可能一开始就跳两步,
当青蛙一开始就跳2步,那么台阶就还剩2个,问题不就又转化为:求2个台阶有多少种跳法。Fun(2)
所以,Fun(4) = Fun(3) + Fun(2)
看到这里,我想你已经彻底理解了这个递推公式的精髓所在了。
这里面也蕴含了一种思想:大事化小的思想,这个不正是我们使用递归的核心思想。通过青蛙的每一步选择都会出现看两种不同的结果,但是每种结果的尽头,台阶数最终不是剩下2个就是1个,都会回到递归的退出条件。
3.题目二(变式)
题目二:一只青蛙一次可以跳上一级台阶,也可以跳上二级台阶...,还可以跳上n级台阶,求该青蛙跳上一个n级的台阶总共需要多少种跳法。
如果你理解上面青蛙跳台阶的思路,那么这道题就不难了。
3.1 分析
这里我就简单分析一下:
与第一道不同的是,青蛙可以这次可以选择跳<=n的步数了,但是,基本的思路是一样的。
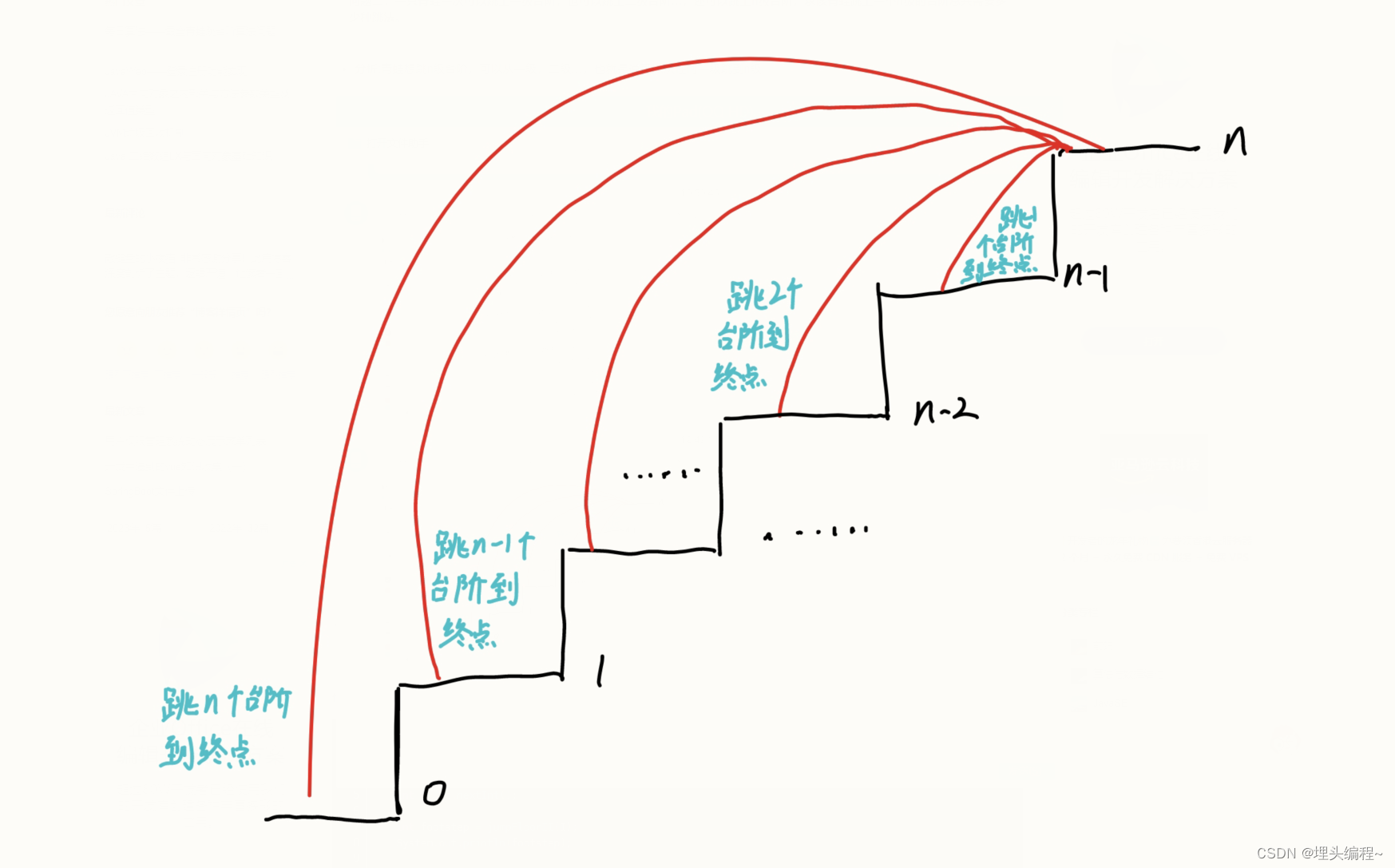
假设有n个台阶,函数Fun用来计算n个台阶有多少种跳法。
那么,我们就可以得到一个递推公式:
Fun(n) = Fun(n-1) + Fun(n-2) + ... + Fun(2) + Fun(1) + 1 ①
Fun(n-1) = Fun(n-2) + Fun(n-3) + ... + Fun(2) + Fun(1) + 1 ②
将上述的①和②结合一下:
Fun(n) = Fun(n-1) + Fun(n-1) = 2*Fun(n-1)
3.2 代码实现
c
#include<stdio.h>
int Fun(int n)
{
if (n == 1)
{
return 1;
}
else
{
return 2*Fun(n - 1);
}
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fun(n);
printf("%d\n", ret);
return 0;
}4. 题目三(变式)
问题三:一只青蛙一次可以跳上一级台阶,也可以跳上二级台阶...,还可以跳上m级台阶,求该青蛙跳上一个n级的台阶总共需要多少种跳法。
4.1 分析
这道题目又和上一道题目有所不同,这次青蛙最多跳<=m个台阶数。
由上两题总结出的思路,我们可以很快地写出此题的递推公式:
Fun(n) = Fun(n-1) + Fun(n-2) + ... + Fun(n-m) ①
Fun(n-1) = Fun(n-2) + Fun(n-3) + ... + Fun(n-m-1) ②
将①和②结合一下:
Fun(n) = 2 * Fun(n-1) + Fun(n-m-1) (n>m)
上述的情况是当n>m时发生的,那么当n<=m时呢?
那问题就会转化为题目二的思路了。
4.2 代码实现
c
int Fun(int n, int m)
{
if (n <= 1) //之所以是小于1,是因为m可能会大于n
{
return 1;
}
if(n>m)
{
return 2 * Fun(n - 1, m) - Fun(n - m - 1, m);
}
return 2 * Fun(n - 1, n); //这里的n不要写成m
}
int main()
{
int n = 0;
int m = 0;
scanf("%d %d", &n, &m);
int ret = Fun(n, m);
printf("%d\n", ret);
return 0;
}后面的两道题希望读者们下来可以慢慢的去琢磨。