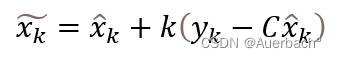一.状态空间方程
系统的状态空间方程描述了系统的动态行为和状态演化过程。它由两个方程组成：状态方程和观测方程。系统的状态空间表达式简写为：
变量描述如下：
- x(t) 是系统的状态向量，表示系统在时间 𝑡的状态。
- 𝑢(𝑡) 是系统的输入向量，表示系统在时间 𝑡的输入。
- 𝑦(𝑡) 是系统的输出向量，表示系统在时间 𝑡的观测输出。
- A 是状态矩阵，描述系统状态的演化规律。
- B 是输入矩阵，描述输入对系统状态的影响。
- C 是观测矩阵，描述状态对观测输出的映射关系。
- D 是直接传递矩阵，描述输入对观测输出的直接影响。
框图如下：
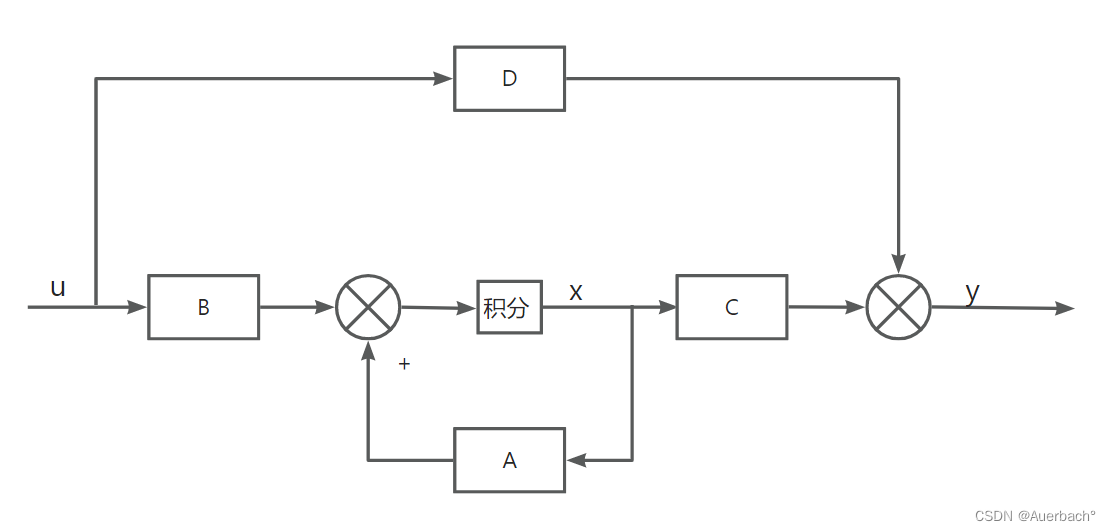
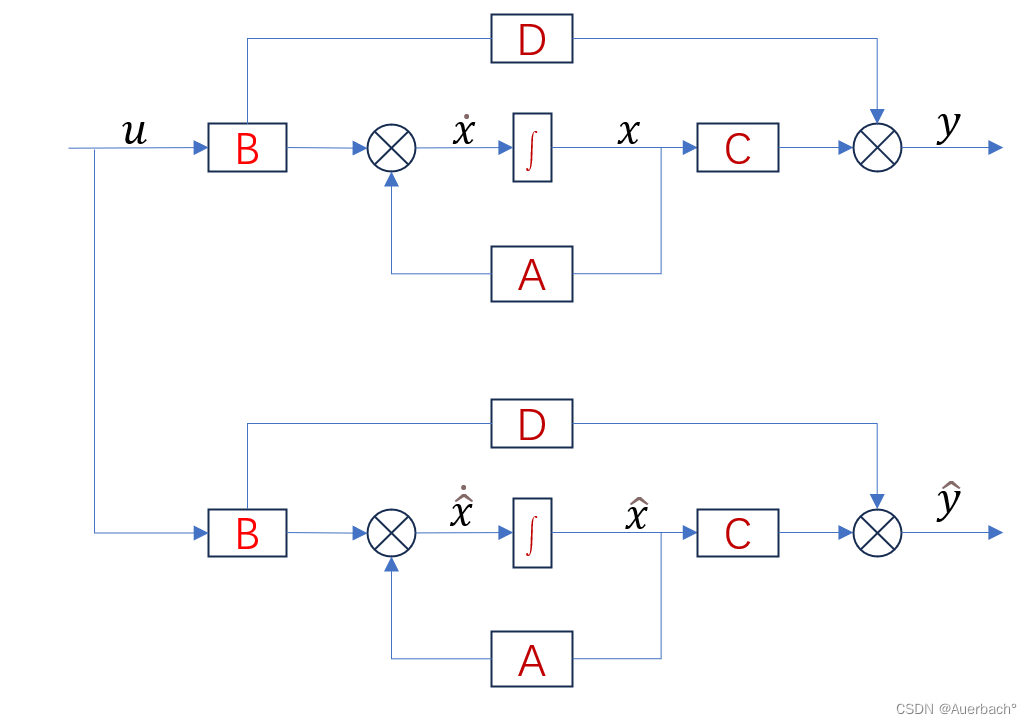
观测器（也称为状态观测器）是一种用于估计系统状态的非递归算法。观测器通常基于系统的输出（观测）和已知的系统模型，通过最小化观测误差来估计系统的状态。观测器可以是线性的或非线性的，它们的设计依赖于系统的特性和观测数据的可用性，下图为一个开环的观测器：
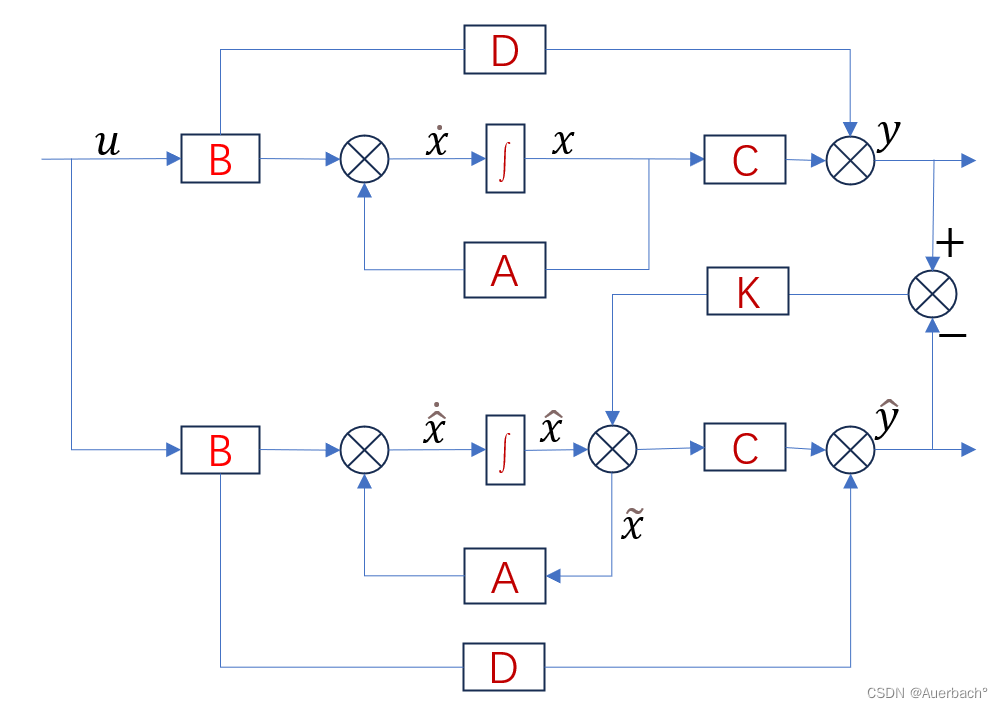
事实上，若没有反馈的话，开环观测器的误差会不断增大，最后导致观测器不再贴合观测的系统，我们可以引入反馈环节用于修正误差。卡尔曼滤波器可以看作是一种特殊的观测器，它利用系统的动态模型和观测数据来估计状态。卡尔曼滤波器中的状态估计和协方差更新步骤与观测器中的状态估计和观测误差最小化步骤类似。在卡尔曼观测器中，反馈增益K就为卡尔曼增益：
其中为引入反馈增益修正后的后验估计，
为先验估计。在没有反馈机制的情况下，观测器的输出不会受到状态估计误差的修正。如果观测噪声较大或者观测模型不准确，观测器的输出可能会与真实状态之间存在较大的误差。随着时间的推移，这些误差可能会逐渐累积并导致状态估计的误差增大。因此在引入反馈增益K的基础上，将上述框图改为离散化得到：
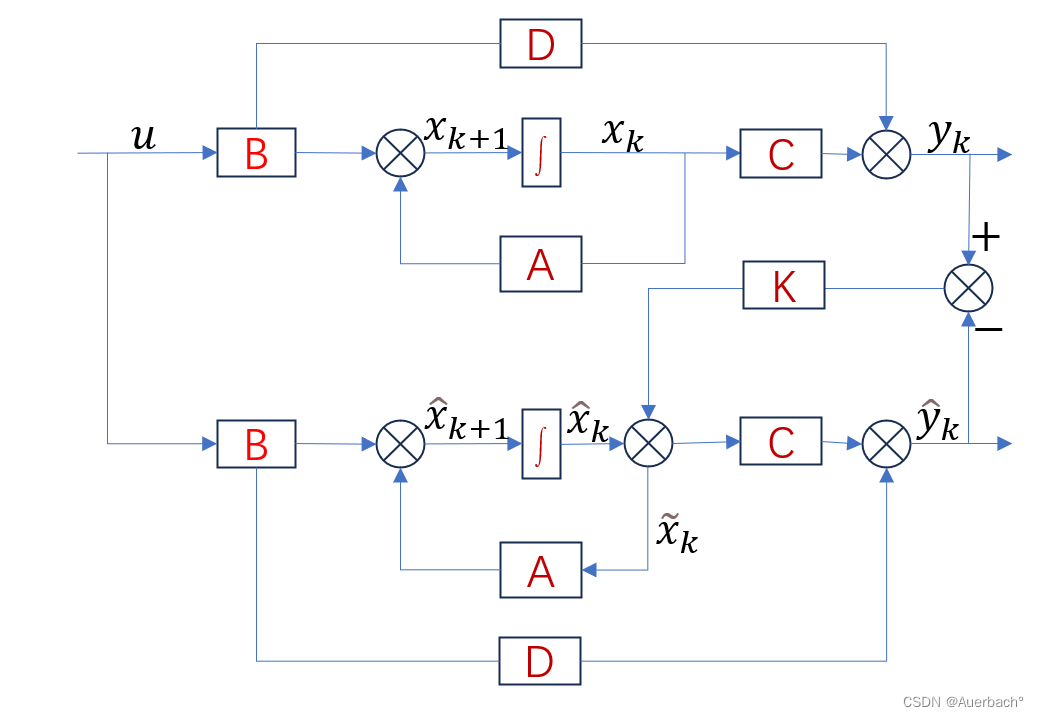
因此，要确定的就是卡尔曼增益K。
二.理论推导部分
由上图可知，卡尔曼滤波器，实际上就是反馈增益K为卡尔曼增益的观测器，核心在于找到一个K使得误差的协方差最小，记后验估计误差如下：
当（
）越小时，也就是误差协方差越小时，观测器越逼近于真实系统，故实际需要求的卡尔曼增益就是使得
（
）最小时的
，即：
考虑过程噪声以及观测噪声，得到系统的状态空间方程：
又由于：
则化简得到：
两边同时加上得到：
记后验误差为：
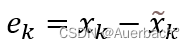
记先验误差为：
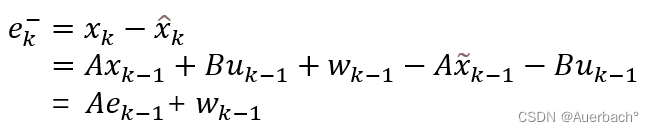
其中为单位矩阵，将本式带入到误差表达式中得到：
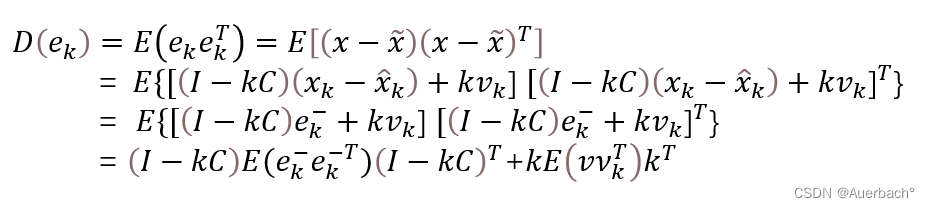
为简化计算，将后验 误差协方差矩阵记作,先验 误差协方差矩阵记作
,观测噪声的协方差矩阵为
得到：
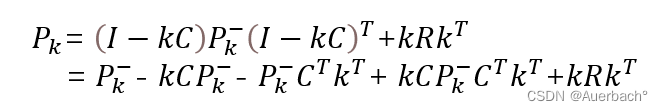
最终要求得的最小化的目标值，实际上就是协方差矩阵对角线的元素和：
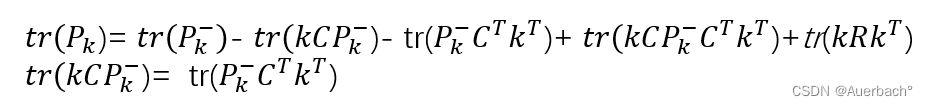
化简得到：
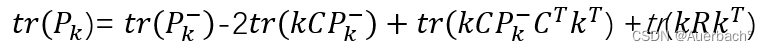
考虑到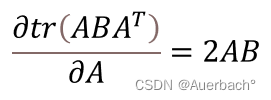
则上述方程对卡尔曼增益求导，解出使误差协方差最小时的卡尔曼增益
：
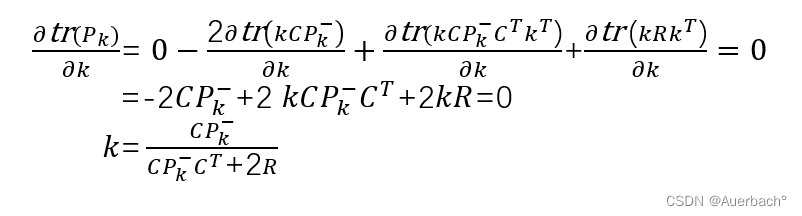
将所求的卡尔曼增益代入到后验 误差协方差矩阵的表达式中得出：
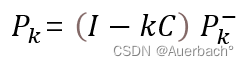
故在上述所有公式中，唯一还没有确定的只剩下先验 误差协方差矩阵，确定过程如下：
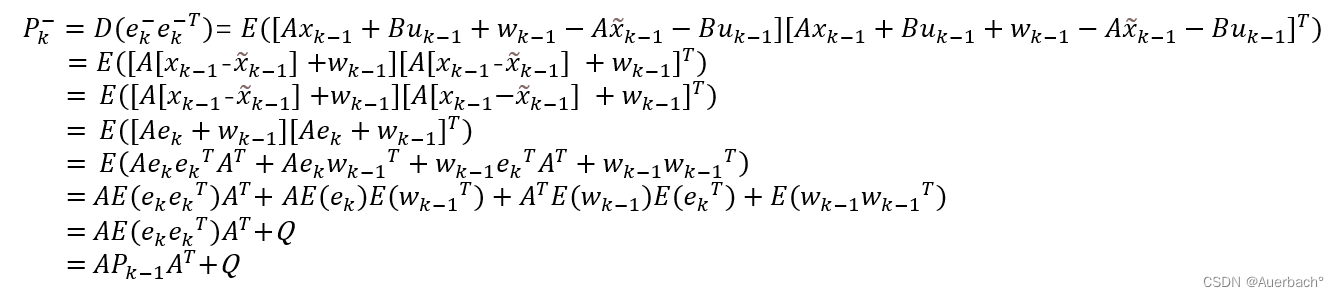
三.总结
至此卡尔曼滤波的五个公式均推导完毕，总结一下就是：
1）状态观测器：
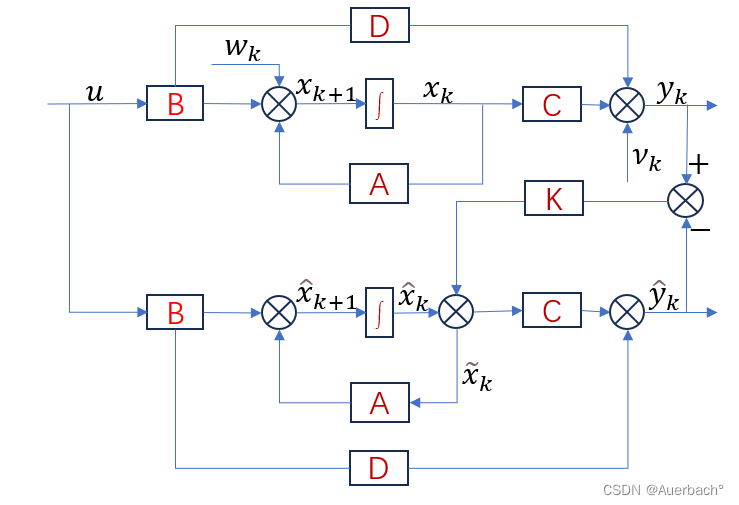
2）预测部分：
①先验估计：
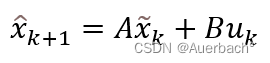
②先验协方差误差：
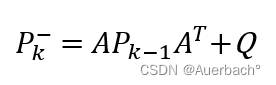
3）校正部分：
①卡尔曼增益:
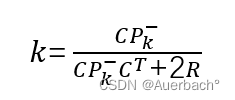
②更新协方差误差：
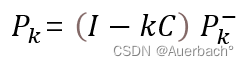
③后验估计：
