几种经典排序算法
在介绍排序之前，先来说说，研究不同的排序主要是要研究他们的哪些不同：
- 时间性能。即排序过程中元素之间的比较次数与元素移动次数。我们此次讨论各种排序方法的时间复杂度时，主要按照最差情况下所需要的比较次数来进行。
- 空间性能。除了存放参加排序的元素之外，排序过程中所需要的其他辅助空间。
- 排序稳定性。对于值相同的两个元素，排序前后的先后次序不变，则称这种排序方法稳定，否则称其不稳定。
然后还有一个概念我们后面会经常提到：趟。排序需要若干遍循环完成，每循环一遍，就叫一趟。
然后，我们今天的例子中，都是以从小到大排序为例的。
另外，因为排序免不了需要交换位置，因此我们先写好一个Swap函数用于交换：
void Swap(int* pa,int* pb)
{
int tmp=*pa;
*pa=*pb;
*pb=tmp;
}
插入排序
动画演示 ：
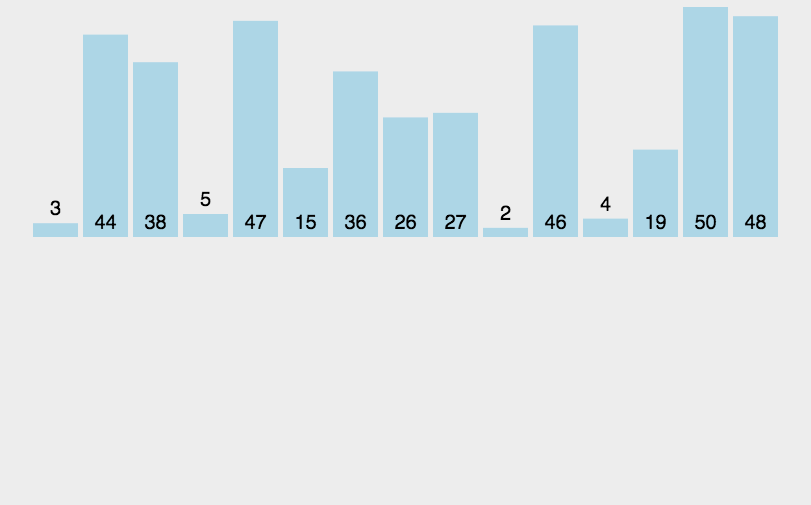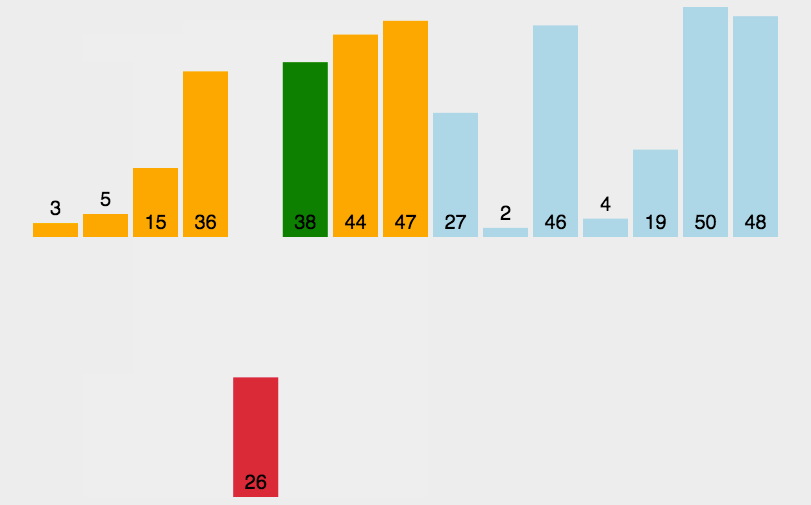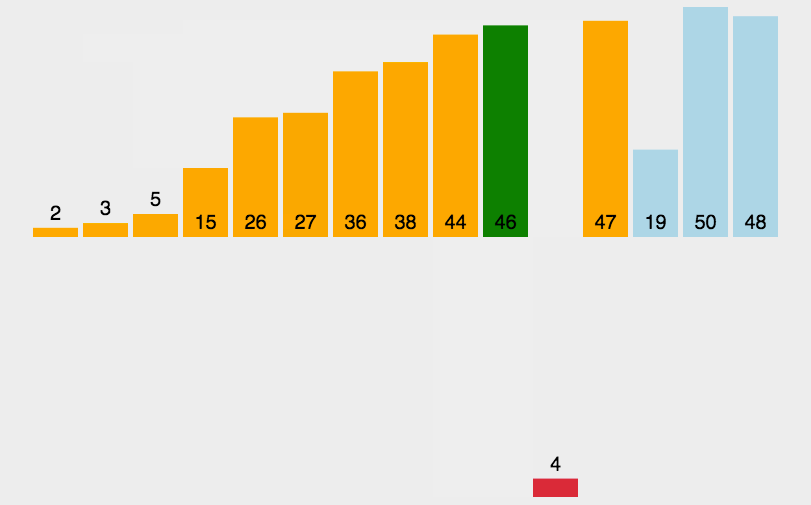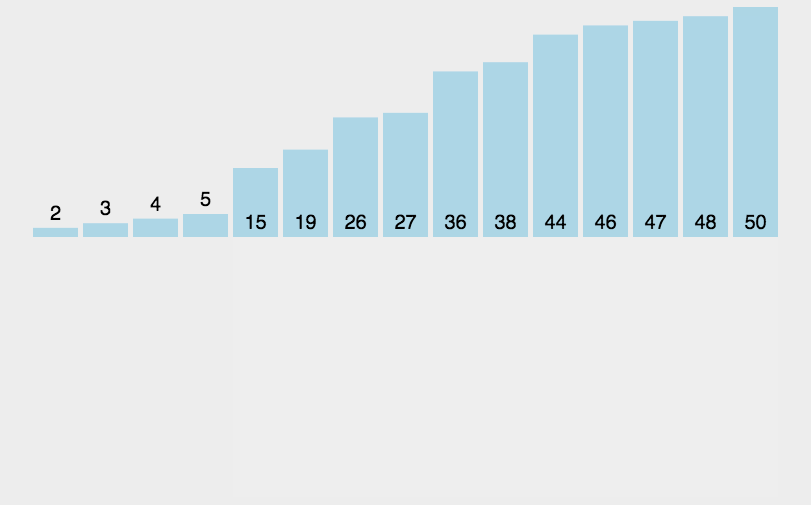
核心思想：
在第i趟排序中，将序列的第i+1个元素，按照值大小，插入到前i个已排好序的序列中。
静态演示：
将【49,38,97,76,65,13,27,50】进行插入排序：
其中红色部分表示已经排好序的部分，花圈元素表示下一趟 要排序的元素。
可以看出来，n个元素，需要n-1趟插入排序才能完全排好。
算法 ：
我们先写一趟排序的算法，然后再加循环。加循环无外就是判断一下起始和结束条件。
c
void insertSort(int k[],int n)//传入要进行排序的数组以及元素数
{
int i,j;//i表示第i趟，也表示当前要调整的元素的下标
//j用来遍历已排好序的序列，用于和第i个元素比较
int tmp=k[i];
for(i=1;i<n;i++)
{
for(j=i-1;j>=0&&k[j]>tmp;j--)
k[j+1]=k[j];
//以上两步用于把比当前元素大的往后调
//一旦检测到已排序好序列中有比当前元素小的，则把当前元素插到该元素后面
k[j+1]=tmp;
}
}我们用【49,38,97,76,65,13,27,50】这个数组检测一下效果：
没毛病，跟我们刚刚手动计算的一样。
排序的时间效率 ：
时间效率主要和排序过程中元素之间的比较次数直接有关。
- 原始序列按值递增：那么每一趟排序，第一次比较，也就是和当前需要调整元素的前一个元素比较时，就跳出循环了，因为比当前需要调整元素小。因此每个元素进行调整时，都只需要比较1次，那么总共有n-1个元素需要调整，就一共比较n-1次。
- 原始序列按值递减：第i趟排序需要和前i个元素都比较一次，因此，整个n-1趟排序需要比较（1+n-1)*(n-1)/ 2=n（n-1）/ 2次
如果以最坏的情况，也就是原始序列递减情况，则插入排序算法的时间复杂度为O（n²）。
由于我们只把比当前元素大 的元素向后调，相等的元素不调，因此调整之后，值相等的两个元素的相对位置在排序前后并未改变，则插入排序算法是稳定的。
由于没有开辟新的空间，因此插入排序算法的空复杂度为O（1）。
折半插入排序法
这个算法的整体思想和插入法一样，只是在找插入位置的时候，用了折半查找的方法，基于前i-1个元素是有序的。
找到位置的标志，也就是某一趟排序中循环停止的标志为high<low,插入位置即为low。
c
void BinInsertSort(int k[],int n)
{
int i,j;
int high,low,mid;
for(i=1;i<n;i++)
{
int tmp=k[i];
high=i-1;
low=0;
while(high>=low)
{
mid=(high+low)/2;
if(tmp>=k[mid])//将相等情况也纳入，保证了稳定性
low=mid+1;
else
high=mid-1;
}
for(j=i;j>low;j--)
k[j]=k[j-1];
k[low]=tmp;
}
}选择排序
动画演示 ：
核心思想 ：
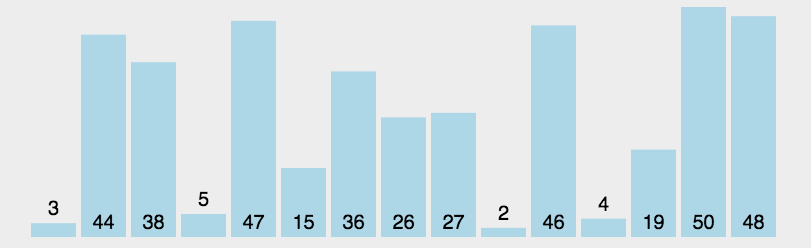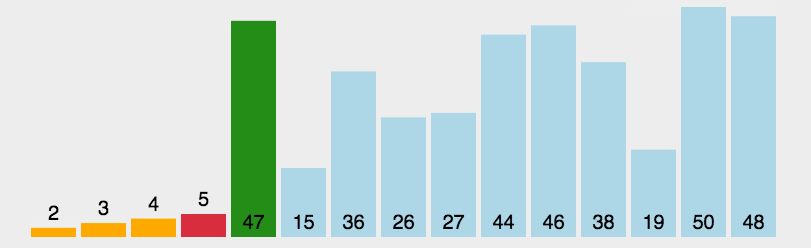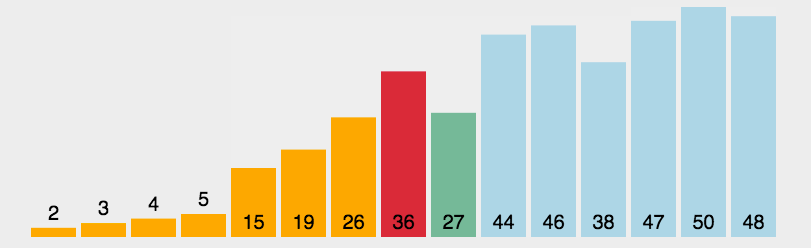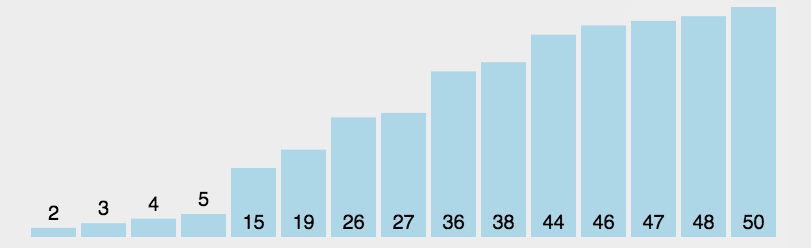
第i趟排序，从序列的后n-i+1个元素中选择一个值最小的元素，将其置于该n-i+1个元素的最前面（与第i个元素交换）
静态演示 ：
红框框起来的表示这一趟中判断出的最小元素，红色部分表示已经排好序的部分。
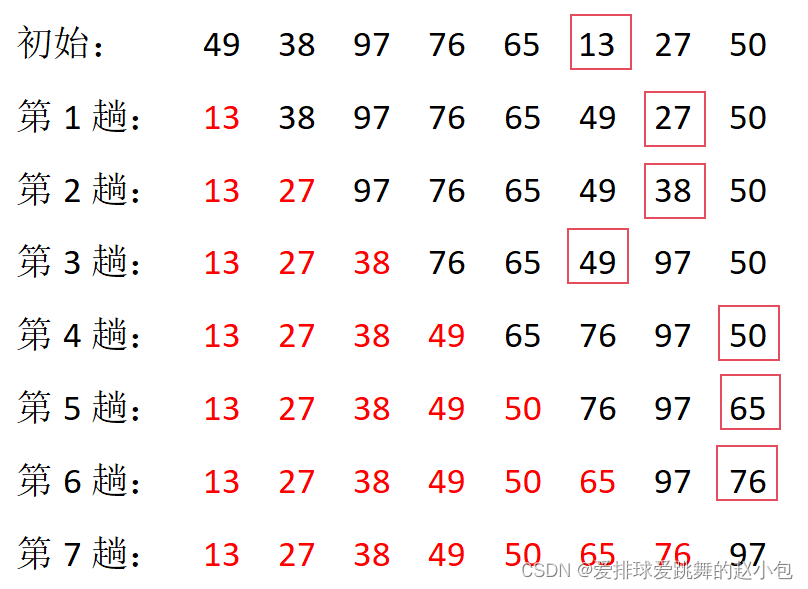共有8个元素，但只排7次。和插入排序一样。
c
void selectsort(int k[],int n)
{
int i,j,d;//d用于记录最小元素的下标
int temp;
for(i=0;i<n-1;i++)
{
d=i;
for(j=i+1;j<n;j++)
{
if(k[j]<k[d])
d=j;
}
Swap(&k[d],&k[i]);
}
}方法2
c
void selectsort2(int k[],int n)
{
int i,j,tmp;
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
if(k[j]<k[i])
Swap(&k[j],&k[i]);
}冒泡排序
动画演示 ：
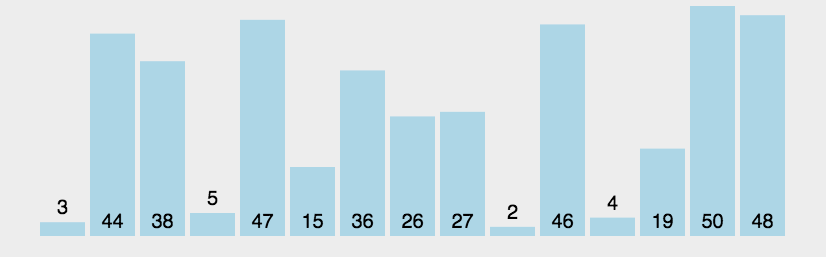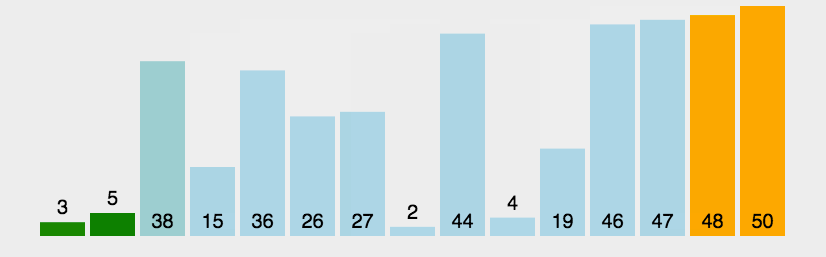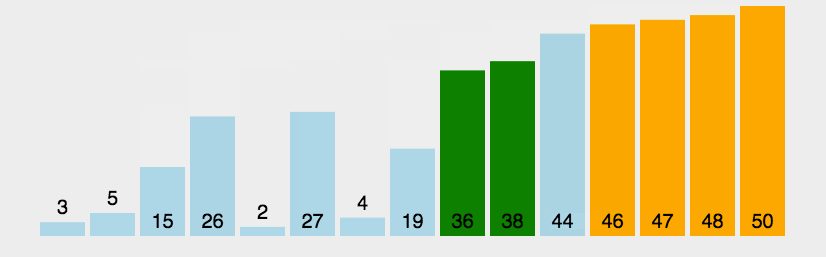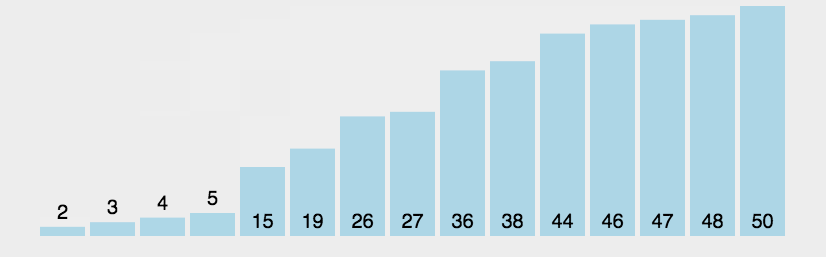
核心思想：第i趟中，对序列的**前n-i+1个元素，从第一个元素开始，相邻的两个元素比较大小，若前者大于后者，则交换。
静态演示 ：
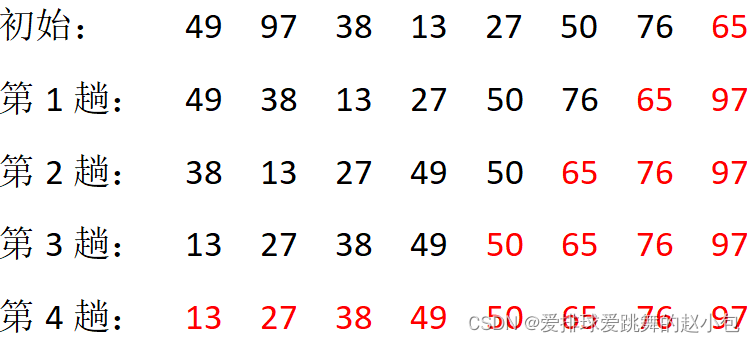
我们发现，选择和插入排序都进行了n-1次，但是为什么冒泡排序小于n-1呢？前两者循环结束的条件都是i，j和n比较，但是冒泡排序，我们需要定义一个变量flag，用于记录，在某趟排序中，是否进行了元素交换。如果进行了，哪怕只有一次，那下一趟循环继续；如果一次也没有，就说明此时序列已经有序，不需要再进行下一趟了。
c
void bubblesort(int k[],int n)
{
int i,j,flag=1;
for(i=n-1;i>0&&flag==1;i--)
{
flag=0;
for(j=0;j<i;j++)
{
if(k[j]>k[j+1])
{
Swap(&k[j],&k[j+1]);
flag=1;
}
}
}
}效率分析 ：
冒泡排序算法的排序趟数和原始序列的排序有关，因此排序趟数为【1，n-1】。
排序趟数最少为1次，即原始序列本身就有序。
最多为n-1次，原始序列为逆序。
因此，冒泡排序的时间复杂度，在最少次数下为O(n),即只进行一轮；在最多次数下为O（n²）
冒泡排序过程中，如果两个数相等，则不进行交换，因此是稳定的。
希尔排序
把整个序列分成若干子序列，每个子序列内部先排序。
在每一趟排序结果均是按照上一趟分好的组（颜色一眼的）进行组内排序的结果（组内排序可以用各种排序方法，插入、冒泡都行）。
每组元素的间隔数满足：
即每一次的gap都是上一次的一半。gap等于1时，整个数组为一个组进行排序，也就是最后一次排序。
每进行一趟排序，数组都会更加接近有序。
我们这里先展示一种组内排序为冒泡排序的希尔排序方法：
c
void shellsort1(int k[],int n)
{
int i,j,flag,gap=n;
//flag用于检测每一趟冒泡排序是否有进行交换，如果没有进行交换，就说明
//数组已经有序了，不用继续进行排序了
int temp;
while(gap>1)
{
gap=gap/2;
do
{
flag=0;
for(i=0;i<n-gap;i++)
{
j=i+gap;
if(k[j]<k[i])
Swap(&k[i],&k[j]);
}
} while (flag==1);
}
}再来展示一种内部排序为插入排序的希尔排序：
c
void shellsort2(int k[],int n)
{
int i,j,temp,gap=n;
while(gap>1)
{
gap=gap/2;
for(i=gap;i<n;i++)
{
temp=k[i];
for(j=i;j>=gap&&k[j-gap]>temp;j-=gap)
k[j]=k[j-gap];
k[j]=temp;
}
}
}效率分析 ：
举个反例就发现，希尔排序是不稳定的了：
【2a,3,4,1,2b,5,6,8】我们让gap=3,则【2a,1,6】是一组，【3,2b,8】是一组，【4,5】一组。
那么第一趟排序的结果就是：
【1,2b,4,2a,3,5,6,8】我们发现，两个2的相对位置发生了变化，因此不稳定。
希尔排序的时间复杂度比较难搞，我们认为在O（nlogn）和O（n²）之间。
堆排序
之前写过一篇专门讲堆排序的文章:link，但是在本次排序专题里，再把它写一次。
动画演示 ：
核心思想 ：先对原始数组进行向下调整 ，从第一个非叶子结点 开始进行。待所有结点都调整完毕之后，形成了一个大堆 ，然后，依次将堆顶和当前堆 的最后个元素交换位置，换完之后进行向下调整。
c
void AjustDown(int k[],int n,int parent)
{
int child=2*parent+1;
while(child<n)
{
if(child+1<n&&k[child+1]>k[child])
++child;
if(k[child]>k[parent])
{
Swap(&k[child],&k[parent]);
parent=child;
child=child*2+1;
}
else
break;
}
}
void heapsort(int k[],int n)
{
for(int i=(n-1-1)/2;i>=0;i--)
{
AjustDown(k,n,i);
}
//建好堆了，下面开始排序
int end=n-1;
while(end>0)
{
Swap(&k[end],&k[0]);
AjustDown(k,end,0);
end--;
}
}效率分析
时间主要消耗在向下调整了，那么每个元素，都要经过向下调整，调整的次数最多为高度次，即logn，有n个元素，则时间复杂度为O（nlogn）。
堆排序显然也不稳定，调整算法压根没有考虑过数组之间的关系，只考虑了堆的结构。
二路归并排序
动画演示 ：
核心思想 ：
第i趟排序将序列的n/2^ (i-1) 个长度为 2^ (i-1) 的有序子序列依次两两合并为n/2^ i 个长度为2^i的有序子序列。
静态演示 ：
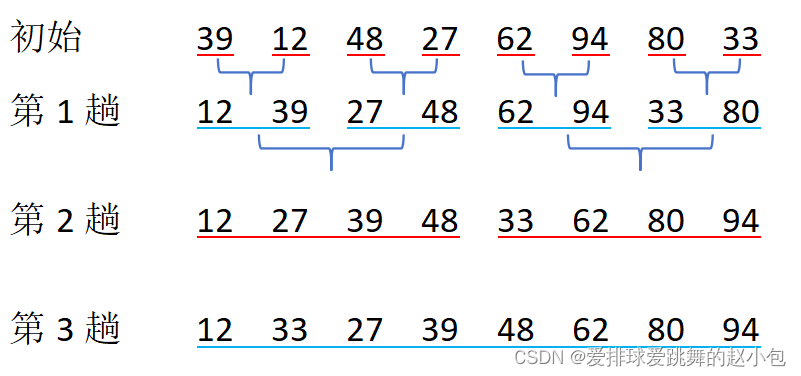
如果n不等于2^ k ，则：
最后一趟在不等长的两个序列中进行就可以。
大家看到这个基本思路，就知道它大概率是要用到递归的思路的，这种一环套一环，每一环的都基于上一环的结果。
从动态图中我们也能看出来，归并排序是需要一个临时数组的，辅助我们为子序列排序。
c
void _mergesort(int k[],int begin,int end,int* tmp)
{
if(begin==end)
return;
int mid=(begin+end)/2;
//[begin,mid][mid+1,end]
_mergesort(k,begin,mid,tmp);
_mergesort(k,mid+1,end,tmp);
//左右都排好以后，我们来合并：
int begin1=begin,end1=mid;
int begin2=mid+1,end2=end;
int i=begin1;
while(begin1<=end1&&begin2<=end)
{
if(k[begin1]<k[begin2])
tmp[i++]=k[begin1++];
else
tmp[i++]=k[begin2++];
}
while(begin1<=end1)
tmp[i++]=k[begin1++];
while(begin2<=end2)
tmp[i++]=k[begin2++];
memcpy(k+begin,tmp+begin,sizeof(int)*(end-begin+1));
}
void mergesort(int k[],int n)
{
int* tmp=(int*)malloc(sizeof(int)*n);
_mergesort(k,0,n-1,tmp);
free(tmp);
tmp=NULL;
}效率分析 ：
当子序列个数为1（n不是2的次幂时为2个），即n/2^ i 为1的时候，排序完成，即排了logn趟。子序列内部排序的时间复杂度主要来源于归并部分的while循环，时间复杂度为O（n），因此，归并排序的时间复杂度为O（nlogn）。
由于开辟了tmp数组，因此空间复杂度时O（n）。
是稳定的。
快速排序
动画演示 ：
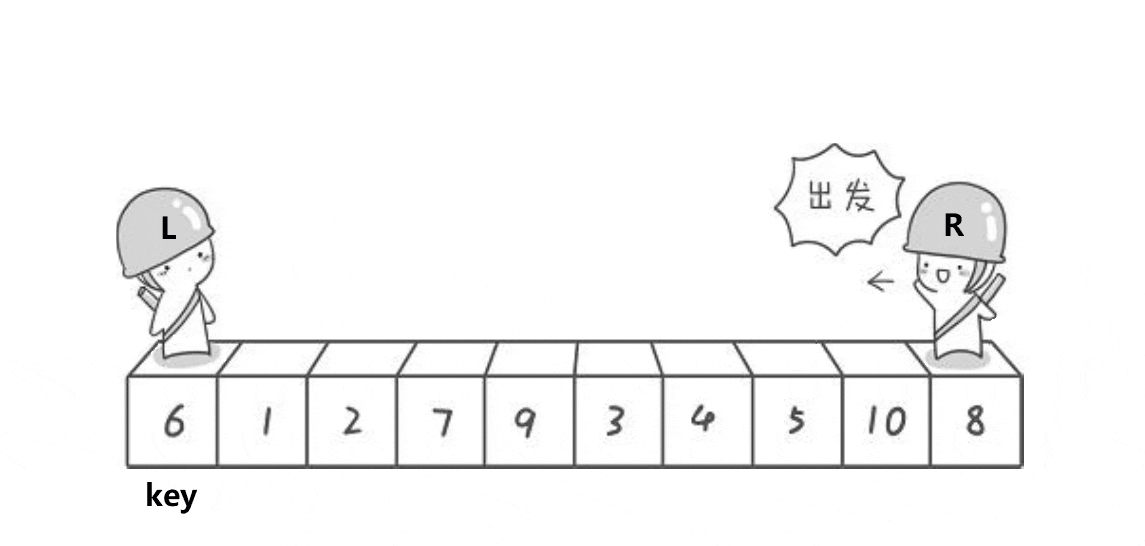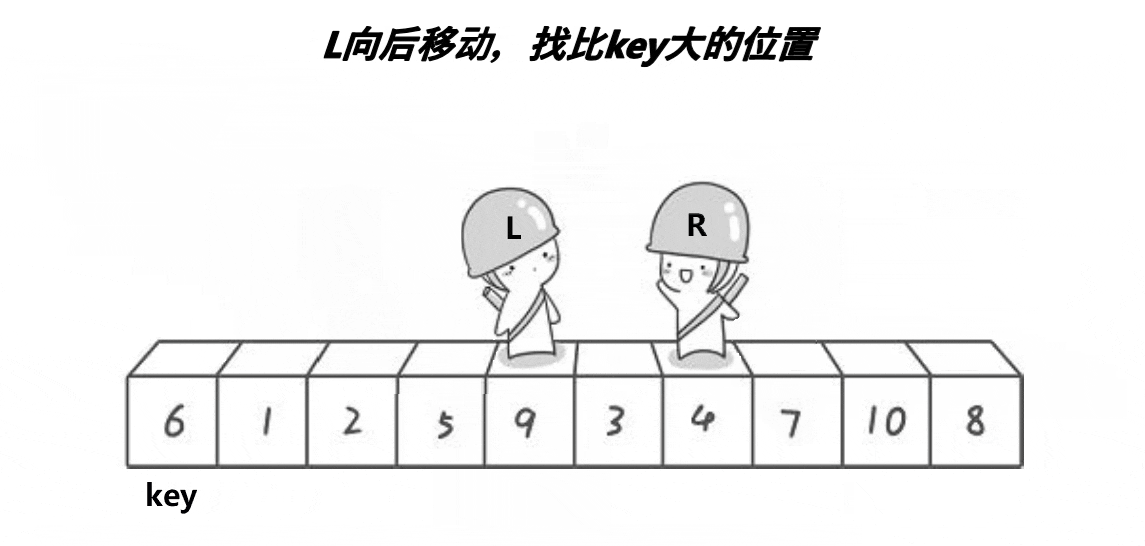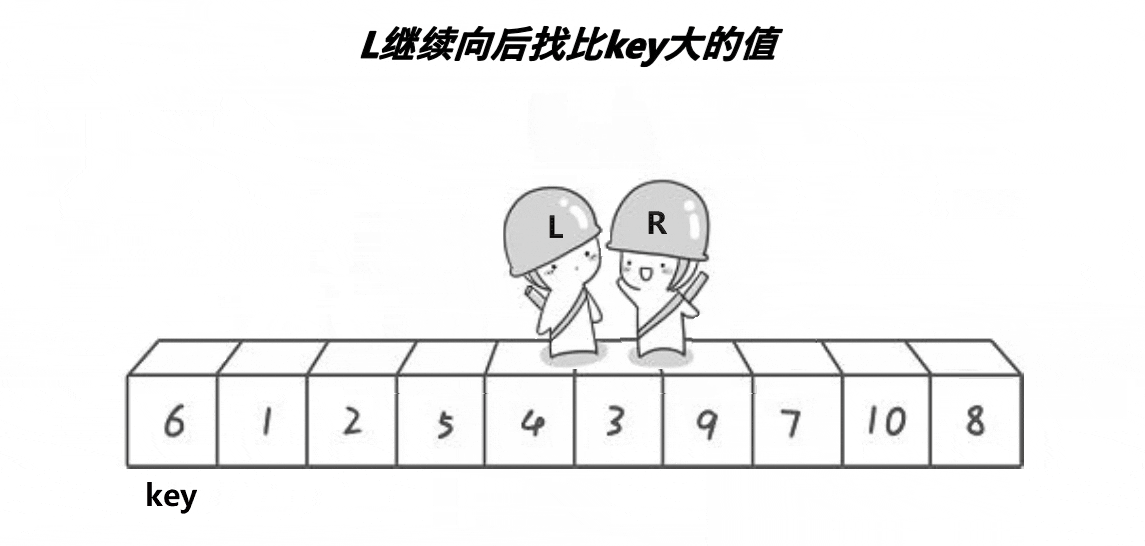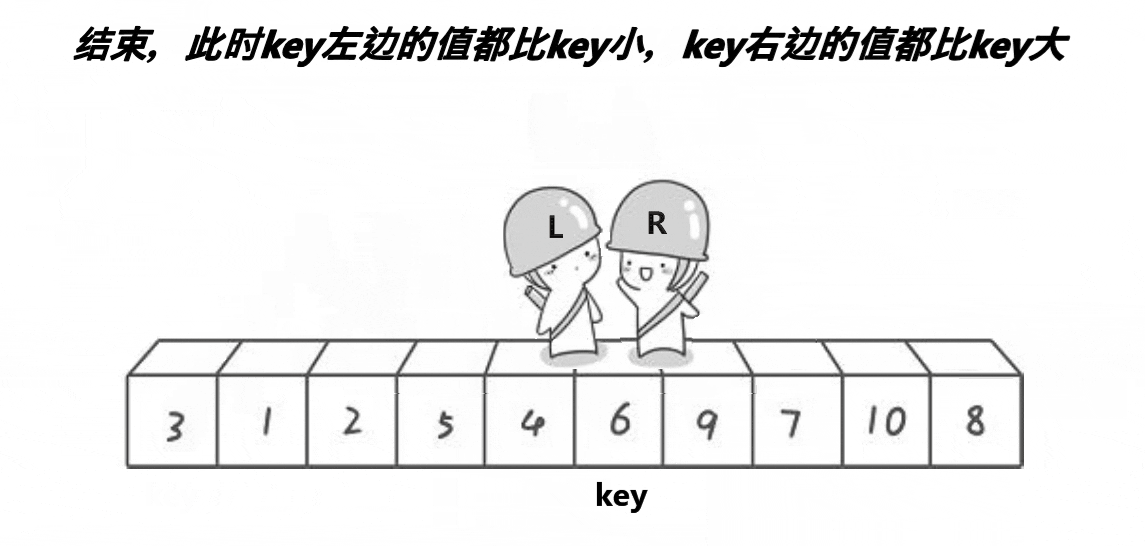为什么右边的先走呢？因为右边的先走可以保证L和R相遇的位置处元素，一定小于key。
c
void quicksort(int k[],int left,int right)
{
if(left>=right)
return;
int begin=left,end=right;
int keyi=left;
while(left<right)
{
//right先走，找比key小的
while(left<right&&k[keyi]<=k[right])//为了防止整个序列里面keyi的右边全部比它大，加一个left<right，以防right一股脑冲出数组头
right--;
//left再走，找比key大的
while(left>right&&k[keyi]>=k[left])
left++;
Swap(&k[left],&k[right]);
}
Swap(&k[left],&k[keyi]);
keyi=left;
//[begin,keyi-1][keyi+1,end]
quicksort(k,begin,keyi-1);
quicksort(k,keyi+1,end);
}效率分析 ：
