1.算法原理(模型)
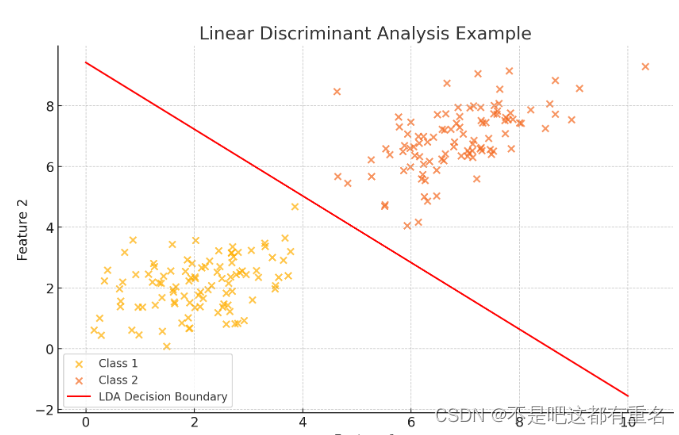
线性判别分析(Linear Discriminant Analysis,LDA)是一种经典的线性学习方法,亦称为Fisher判别分析。
LDA 的思想:
给定训练样本集,将全体样本投影到一条直线上,使的:
- 同类样例的投影点总体尽可能接近/同类样本的方差尽可能小;
- 异类样本的投影点总体尽可能远离/异类样本的中心尽可能远;
2.损失函数推导(策略)
2.0 补充
1.范数(Norm) 是一个在向量空间中用于量度向量大小的函数。它满足以下性质:
- 非负性 :对于任何向量x,有||x|| ≥ \geq ≥ 0且||x||=0当且仅当x=0;
- 齐次性 (正齐次性):对于任何标量 α \alpha α和任何向量x,有 ∣ ∣ α x ∣ ∣ = ∣ α ∣ ∣ ∣ x ∣ ∣ ||\alpha x||=|\alpha|||x|| ∣∣αx∣∣=∣α∣∣∣x∣∣
- 三角不等式 :对于任何向量x和y,有 ∣ ∣ x + y ∣ ∣ ≤ ∣ ∣ x ∣ ∣ + ∣ ∣ y ∣ ∣ ||x+y||\leq||x||+||y|| ∣∣x+y∣∣≤∣∣x∣∣+∣∣y∣∣
一般的p-范数定义为:
∥ x ∥ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 p \|\mathbf{x}\|p = \left( \sum{i=1}^{n} |x_i|^p \right)^{\frac{1}{p}} ∥x∥p=(∑i=1n∣xi∣p)p1
2.协方差和协方差矩阵:
方差和协方差是统计学中用于描述数据分布和关系的重要指标。
方差
方差是描述一个随机变量 的离散程度的度量,表示数据点与均值之间的偏离程度。
公式
样本方差:
s 2 = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) 2 s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 s2=n−11∑i=1n(xi−xˉ)2
总体方差:
σ 2 = 1 N ∑ i = 1 N ( x i − μ ) 2 \sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2 σ2=N1∑i=1N(xi−μ)2
协方差
协方差是描述两个随机变量 之间的线性关系的度量。它反映了一个变量变化时另一个变量的变化方向。
公式
样本方差:
cov ( X , Y ) = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) \text{cov}(X, Y) = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) cov(X,Y)=n−11∑i=1n(xi−xˉ)(yi−yˉ)
总体方差:
σ X Y = 1 N ∑ i = 1 N ( x i − μ X ) ( y i − μ Y ) \sigma_{XY} = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu_X)(y_i - \mu_Y) σXY=N1∑i=1N(xi−μX)(yi−μY)
协方差矩阵:
| 协方差矩阵 | x 1 x_1 x1 | x 2 x_2 x2 |
|---|---|---|
| x 1 x_1 x1 | cov ( x 1 , x 1 ) \text{cov}(x_1, x_1) cov(x1,x1) | cov ( x 1 , x 2 ) \text{cov}(x_1, x_2) cov(x1,x2) |
| x 2 x_2 x2 | cov ( x 2 , x 1 ) \text{cov}(x_2, x_1) cov(x2,x1) | cov ( x 2 , x 2 ) \text{cov}(x_2, x_2) cov(x2,x2) |
2.1推导过程
设要投影的直线为 ω \boldsymbol \omega ω, μ 0 , μ 1 \mu_0,\mu_1 μ0,μ1分别表示反例集合和正例集合的均值向量 , θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1分别表示反例集合和正例集合的均值向量与投影直线的夹角, 围绕上面思想中的中心 和方差 两个点来进行推导:
1.异类样本的中心要尽可能远:
∣ μ 0 ∣ c o s θ 表示 μ 0 到 ω 的投影的长 |\mu_0|cos\theta 表示\mu_0到\omega的投影的长 ∣μ0∣cosθ表示μ0到ω的投影的长
为了实现异类样本的中心尽可能的远,那么就应该求下式:
m a x ∣ ∣ ( ∣ μ 0 ∣ c o s θ − ∣ μ 1 ∣ c o s θ ) ∣ ∣ 2 2 max||(|\mu_0|cos\theta-|\mu_1|cos\theta)||^2_2 max∣∣(∣μ0∣cosθ−∣μ1∣cosθ)∣∣22
在看上面的式子,发现这个 θ \theta θ不好得到,那就进一步化,在上式中乘以一个常量(不会影响求最大值) ∣ ω ∣ |\omega| ∣ω∣,注意这里是减完之后是个向量,因此要用到范数来衡量向量大小 ,而平方是为了简化计算,得到,
m a x ∣ ∣ ( ∣ ω ∣ ∣ μ 0 ∣ c o s θ − ∣ ω ∣ ∣ μ 1 ∣ c o s θ ) ∣ ∣ 2 2 max||(|\omega||\mu_0|cos\theta-|\omega||\mu_1|cos\theta)||^2_2 max∣∣(∣ω∣∣μ0∣cosθ−∣ω∣∣μ1∣cosθ)∣∣22
即得到,
m a x ∣ ∣ ω T μ 0 − ω T μ 1 ∣ ∣ 2 2 max||\omega^T\mu_0-\omega^T\mu_1||^2_2 max∣∣ωTμ0−ωTμ1∣∣22
2.同类样本的方差要尽可能小:
m i n ( ω T ( ∑ 0 + ∑ 1 ) ω ) min({\omega^T(\sum_0+\sum_1)\omega}) min(ωT(0∑+1∑)ω)
最终得到损失函数:
m a x J = m a x ( ∣ ∣ ω T μ 0 − ω T μ 1 ∣ ∣ 2 2 ω T ∑ 0 ω + ω T ∑ 1 ω ) − − − − − − − − − − − − − = m a x ( ∣ ∣ ( ω T μ 0 − ω T μ 1 ) T ∣ ∣ 2 2 ω T ( ∑ 0 + ∑ 1 ) ω ) − − − − − − − − − − − − − = m a x ( ∣ ∣ ( μ 0 − μ 1 ) T ω ∣ ∣ 2 2 ω T ( ∑ 0 + ∑ 1 ) ω ) − − − − − − − − − − − − − = m a x ( [ ( μ 0 − μ 1 ) T ω ] T ( μ 0 − μ 1 ) T ω ω T ( ∑ 0 + ∑ 1 ) ω ) − − − − − − − − − − − − − = m a x ( ω T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T ω ω T ( ∑ 0 + ∑ 1 ) ω ) maxJ =max(\frac{||\omega^T\mu_0-\omega^T\mu_1||^2_2}{\omega^T\sum_0\omega+\omega^T\sum_1\omega})\newline -------------\newline =max(\frac{||(\omega^T\mu_0-\omega^T\mu_1)^T||^2_2}{\omega^T(\sum_0+\sum_1)\omega})\newline -------------\newline =max(\frac{||(\mu_0-\mu_1)^T\omega||^2_2}{\omega^T(\sum_0+\sum_1)\omega})\newline -------------\newline =max(\frac{[(\mu_0-\mu_1)^T\omega]^T(\mu_0-\mu_1)^T\omega}{\omega^T(\sum_0+\sum_1)\omega})\newline -------------\newline =max(\frac{\omega^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T\omega}{\omega^T(\sum_0+\sum_1)\omega})\newline maxJ=max(ωT∑0ω+ωT∑1ω∣∣ωTμ0−ωTμ1∣∣22)−−−−−−−−−−−−−=max(ωT(∑0+∑1)ω∣∣(ωTμ0−ωTμ1)T∣∣22)−−−−−−−−−−−−−=max(ωT(∑0+∑1)ω∣∣(μ0−μ1)Tω∣∣22)−−−−−−−−−−−−−=max(ωT(∑0+∑1)ω[(μ0−μ1)Tω]T(μ0−μ1)Tω)−−−−−−−−−−−−−=max(ωT(∑0+∑1)ωωT(μ0−μ1)(μ0−μ1)Tω)
第一步到第二步是可以这么理解:1*1的向量转置不变。
进一步,把上面的式子的中间部分记作 S b S_b Sb,下面式子的中间部分记作 S w S_w Sw,得到:
m a x J = w T S b w w T S w w maxJ=\frac{w^TS_bw}{w^TS_ww} maxJ=wTSwwwTSbw
转化为最小化:
m i n − w T S b w s . t . w T S w w = 1 min -w^TS_bw \newline s.t. \ w^TS_ww=1 min−wTSbws.t. wTSww=1
3.求解w(算法)
3.0 补充:拉格朗日乘子法
拉格朗日乘子法是一种在约束条件下求解多元函数极值的数学方法。它通过引入拉格朗日乘子,将约束优化问题转换为无约束优化问题。该方法特别适用于等式约束的情况。
拉格朗日乘子法的步骤
**1.构造拉格朗日函数:**将目标函数和约束条件结合,形成拉格朗日函数。
L ( x 1 , x 2 , ... , x n , λ 1 , λ 2 , ... , λ m ) = f ( x 1 , x 2 , ... , x n ) + ∑ i = 1 m λ i g i ( x 1 , x 2 , ... , x n ) \mathcal{L}(x_1,x_2, \ldots, x_n, \lambda_1, \lambda_2, \ldots, \lambda_m) = f(x_1, x_2, \ldots, x_n) + \sum_{i=1}^{m} \lambda_i g_i(x_1, x_2, \ldots, x_n) L(x1,x2,...,xn,λ1,λ2,...,λm)=f(x1,x2,...,xn)+i=1∑mλigi(x1,x2,...,xn)
**2.求拉格朗日函数的偏导数:**对所有变量求偏导数,并令这些偏导数等于零,得到一组方程。
∂ L ∂ x j = 0 ( j = 1 , 2 , ... , n ) \frac{\partial \mathcal{L}}{\partial x_j} = 0 \quad (j = 1, 2, \ldots, n) ∂xj∂L=0(j=1,2,...,n)
∂ L ∂ λ i = 0 ( i = 1 , 2 , ... , m ) \frac{\partial \mathcal{L}}{\partial \lambda_i} = 0 \quad (i = 1, 2, \ldots, m) ∂λi∂L=0(i=1,2,...,m)
3.解方程组: 通过解上一步得到的方程组,得到值。
3.1求解w过程
由拉格朗日乘子法可得到拉格朗日函数为:
L ( w , λ ) = − w T S b w + λ ( w T S w w − 1 ) L(w,\lambda)=-w^TS_bw+\lambda(w^TS_ww-1) L(w,λ)=−wTSbw+λ(wTSww−1)
对w求偏导得到(使用矩阵微分公式)
∂ L ( w , λ ) ∂ w = − ∂ ( w T S b w ) ∂ w + λ ∂ ( w T S w w − 1 ) ∂ w − − − − − − − = − ( S b + S b T ) w + λ ( S W + S w T ) w − − − − − − − = − 2 S b w + 2 λ S w w \frac{\partial L(w,\lambda)}{\partial w}=-\frac{\partial(w^TS_bw)}{\partial w}+\lambda\frac{\partial(w^TS_ww-1)}{\partial w}\newline -------\newline=-(S_b+S_b^T)w+\lambda(S_W+S_w^T)w\newline -------\newline=-2S_bw+2\lambda S_ww ∂w∂L(w,λ)=−∂w∂(wTSbw)+λ∂w∂(wTSww−1)−−−−−−−=−(Sb+SbT)w+λ(SW+SwT)w−−−−−−−=−2Sbw+2λSww
令上式等于0得到,
− 2 S b w + 2 λ S w w = 0 -2S_bw+2\lambda S_ww=0 −2Sbw+2λSww=0
λ S w w = S b w \lambda S_ww=S_bw λSww=Sbw
λ S w w = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w \lambda S_ww=(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw λSww=(μ0−μ1)(μ0−μ1)Tw
若令 ( μ 0 − μ 1 ) T w = γ (\mu_0-\mu_1)^Tw=\gamma (μ0−μ1)Tw=γ(一个数),则
λ S w w = ( μ 0 − μ 1 ) γ \lambda S_ww=(\mu_0-\mu_1)\gamma λSww=(μ0−μ1)γ
w = γ λ S w − 1 ( μ 0 − μ 1 ) w=\frac \gamma \lambda S_w^{-1}(\mu_0-\mu_1) w=λγSw−1(μ0−μ1)
由于不关心w的大小只关心方向,所以可令 γ = λ \gamma=\lambda γ=λ,即得到最终的求解公式。
4.广义特征值和广义利瑞商
4.1广义特征值
设A,B为n阶方阵,若存在数 λ \lambda λ,使得方程 A x = λ B x Ax=\lambda Bx Ax=λBx存在非零解,则称 λ \lambda λ为A相对于B 的广义特征值,x为A 相对于B的属于广义特征值 λ \lambda λ的特征向量。特别的,当B=I(单位矩阵)时,广义特征值问题退化为标准特征值问题。
4.2广义利瑞商
设A,B为n阶厄米(Hermitian)矩阵,且B 正定,称 R ( x ) = x H A x x H B x ( x ≠ 0 ) R(x)=\frac{x^HAx}{x^HBx}(x\neq0) R(x)=xHBxxHAx(x=0)为A相对于B 的广义瑞利商。特别的,当B=I(单位矩阵)时,广义瑞利商退化为瑞利商。
性质:
设 λ i , x i ( i = 1 , 2 , . . . , n ) \lambda_i,x_i(i=1,2,...,n) λi,xi(i=1,2,...,n)为A相对于B的广义特征值和特征向量,且 λ 1 ≤ λ 2 ≤ . . . ≤ λ n \lambda_1\leq\lambda_2\leq...\leq\lambda_n λ1≤λ2≤...≤λn。
m i n x ≠ 0 R ( x ) = x H A x x H B x = λ 1 , x ∗ = x 1 min_{x\neq 0}R(x)=\frac{x^HAx}{x^HBx}=\lambda_1,x^*=x_1 minx=0R(x)=xHBxxHAx=λ1,x∗=x1
m a x x ≠ 0 R ( x ) = x H A x x H B x = λ n , x ∗ = x n max_{x\neq 0}R(x)=\frac{x^HAx}{x^HBx}=\lambda_n,x^*=x_n maxx=0R(x)=xHBxxHAx=λn,x∗=xn
上述性质可用来证明多分类线性判别分析