机器人控制系列教程之串联机器人工作空间

简介

在机器人学领域，对机器人工作空间的精确分析是实现高效、安全操作的关键。工作空间是指机器人末端执行器在不与环境或其他物体发生碰撞的情况下能够到达的所有位置的集合。为了求解这一空间，研究者们发展了多种方法，包括作图法、蒙特卡洛法、极值法、数值法和解析法等。这些方法各有优势，适用于不同的应用场景和需求。

求解

两个基本问题：

给出机器人的结构形式、结构参数以及关节变量的变化范围，求解工作空间。称为工作空间分析或工作空间正问题。
给出某一限定的工作空间，求其结构形式、参数等，称为工作空间综合或工作空间逆问题。

机器人的工作空间求解方法主要有解析法、图解法和数值法。

解析法。是通过包络曲线来确定工作空间的边界线，该方法虽然可以通过约束方程求解边界，但由于表达式过于复杂，而且直观性不强，一般只适合于关节少的机器人。
图解法。可以直观的看出工作空间的剖截面，但对于有冗余机器人，无法准确的描述机器人的工作空间。
数值法。计算机器人的工作空间，实际上选取尽可能多的独立的关节变量的组合，再利用正解运动学方程计算机器人手臂末端点的坐标值，这些坐标值就形成了机器人的工作空间。

数值法中的蒙特卡洛法是一种简单、实用的方法，目前已得到了广泛的应用。蒙特卡洛法： 是一种借助于随机抽样来解决数学问题的数值方法，在工程上被广泛应用于描述某些随机的物理现象，通常在机器人的研究中被应用于机器人误差分析、工作空间求解等方面。

工作空间求解步骤： 蒙特卡洛法应用于机器人工作空间求解，关键之处在于机器人的各关节是在其相应取值范围内工作的，当所有关节在取值范围内随机遍历取值后，末端点的所有随机值的集合就构成了机器人的工作空间。其具体步骤如下：

求解机器人的运动学方程正解。根据正解求得机器人手腕末端点在参考坐标系中的位置向量。由于我们只需要末端点的空间位置，因此没有必要考虑末端姿态.
确定各个关节的运动变化范围，采用Rand()函数在各关节运动范围内产生一系列随机数值作为随机步长变量；
将所求关节角随机值代入到正运动学方程中，可得末端点对应的位置向量；
将得到的机器人末端点位置向量值由 Matlab 绘成三维图像。

结果显示

利用MATLAB机器人工具箱，可进行如下编写，其中UR5机器人模型程序编写请见：

clear,clc,close all;
%% 建立机器人DH参数，初始状态为竖直状态
L1=Link('d',162.50,'a',0,'alpha',0,'modified');
L2=Link('d',0,'a',0,'alpha',pi/2,'offset',pi/2,'modified');
L3=Link('d',0,'a',425,'alpha',0,'modified');
L4=Link('d',126.70+6.6,'a',392.25,'alpha',0,'offset',pi/2,'modified');
L5=Link('d',99.70,'a',0,'alpha',pi/2,'modified');
L6=Link('d',99.60-4.5,'a',0,'alpha',-pi/2,'modified');

%采用弧度制
L(1).qlim=[-180,180]/180*pi;
L(2).qlim=[-145,65]/180*pi;
L(3).qlim=[-65,220]/180*pi;
L(4).qlim=[-180,180]/180*pi;
L(5).qlim=[-135,135]/180*pi;
L(6).qlim=[-360,360]/180*pi;


robot=SerialLink([L1 L2 L3 L4 L5 L6],'name','UR5')

num=30000;
P=zeros(num,3);
for i =1:num
    q1=L(1).qlim(1)+rand*(  L(1).qlim(2) - L(1).qlim(1)  );
    q2=L(2).qlim(1)+rand*(  L(2).qlim(2) - L(2).qlim(1)  );
    q3=L(3).qlim(1)+rand*(  L(3).qlim(2) - L(3).qlim(1)  );
    q4=L(4).qlim(1)+rand*(  L(4).qlim(2) - L(4).qlim(1)  );
    q5=L(5).qlim(1)+rand*(  L(5).qlim(2) - L(5).qlim(1)  );
    q6=L(6).qlim(1)+rand*(  L(6).qlim(2) - L(6).qlim(1)  );
    
    q=[q1 q2 q3 q4 q5 q6];
    T=robot.fkine(q);
    P(i,:)=transl(T);
end
plot3(P(:,1),P(:,2),P(:,3),'b.','markersize',1);
hold on
grid on
daspect([1 1 1]);
view([45 45]);
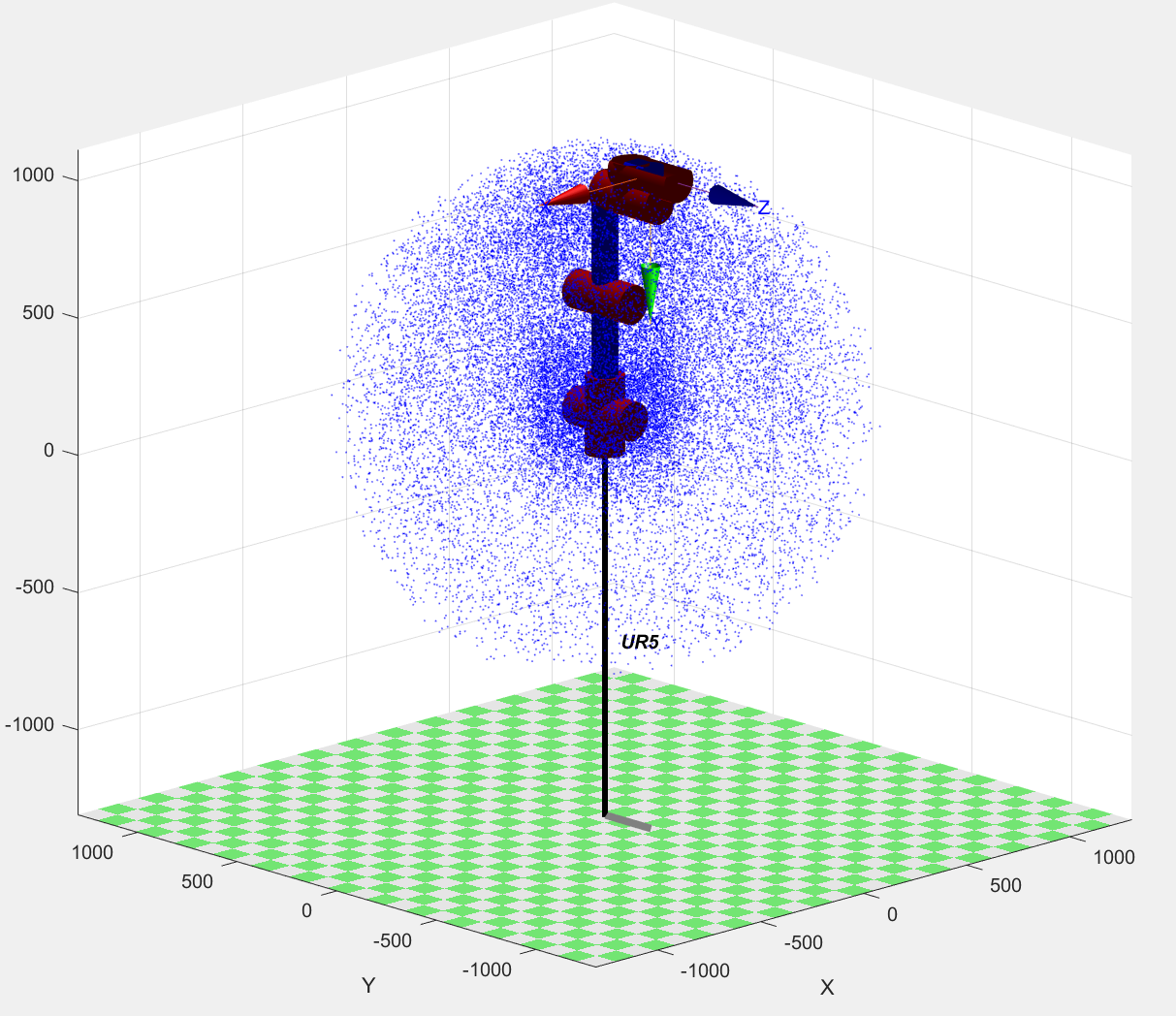
robot.plot([0 0 0 0 0 0])

可得：

机器人控制系列教程之串联机器人工作空间

简介

分类

求解

结果显示

往期推荐