算法金 | 线性回归：不能忽视的五个问题

大侠幸会，在下全网同名「算法金」 0 基础转 AI 上岸，多个算法赛 Top 「日更万日，让更多人享受智能乐趣」

1. 线性回归的理论依据是什么？
2. 多重共线性是什么，它如何影响线性回归模型？
3. 什么是自相关性，自相关性对线性回归有什么影响？
4. 什么是异方差性，如何检测和处理异方差性？
5. 训练数据与测试数据分布不一致会带来什么问题，如何确保数据分布一致性？

1. 线性回归的理论依据是什么？

定义和背景

线性回归是一种统计方法，用于研究因变量 𝑌 和一个或多个自变量 𝑋 之间的线性关系。其理论依据主要基于以下几个方面：

1. 最小二乘法（OLS）：线性回归通过最小化残差平方和（即观测值与预测值之间的差值的平方和）来确定最佳拟合直线。这种方法称为最小二乘法。
2. 假设前提：线性回归模型的应用依赖于一些关键假设，包括线性关系、同方差性、独立性和正态性。

线性回归的本质在于通过假设因变量和自变量之间存在线性关系，并通过最小化残差平方和来确定最佳拟合模型。虽然这些假设在现实中可能并不总是严格成立，但它们提供了一个简单而有效的方法来分析和预测数据。理解这些理论依据和假设条件，有助于更好地应用线性回归模型，并在实际中识别和处理潜在的问题。

2. 多重共线性是什么，它如何影响线性回归模型？

定义和背景

多重共线性指的是在回归分析中，当自变量之间存在高度线性相关性时，导致其中一个自变量可以被另一个或多个自变量近似线性表示的现象。

详细解答

多重共线性的影响

1. 不稳定的回归系数：当存在多重共线性时，回归系数的估计值会变得非常不稳定，对应的标准误差会增大。这意味着即使输入数据有微小的变化，回归系数的估计值也会发生很大的变化。
2. 显著性检验失效：多重共线性会导致回归系数的显著性检验失效，具体表现为回归模型的总体检验（F检验）可能表明模型显著，但单个回归系数的t检验却显示不显著。这使得我们难以判断哪些自变量对因变量有实际的影响。
3. 解释力下降：由于回归系数的不稳定和显著性检验的失效，模型的解释力会下降。这使得我们难以准确地解释每个自变量对因变量的贡献。
4. 共线性增加模型的复杂度：高度共线的自变量在模型中可能带来冗余信息，增加模型的复杂度，进而影响模型的泛化能力。

如何检测和处理多重共线性

1. 方差膨胀因子（VIF）：检测多重共线性最常用的方法之一是计算方差膨胀因子（VIF）。VIF的公式如下：

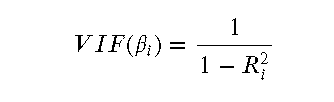
1. 其中，𝑅2𝑖是在预测第 𝑖 个自变量时，其他自变量作为自变量的回归模型的决定系数。一般来说，如果 VIF > 10，说明存在严重的多重共线性问题。
2. 特征选择：可以通过特征选择的方法，去除冗余或高度相关的自变量。例如，递归特征消除（RFE）或使用 Lasso 回归来减少特征数量。
3. 主成分分析（PCA）：使用主成分分析将自变量进行降维，通过提取主成分来替代原始的自变量，减小多重共线性的影响。
4. 数据标准化：对自变量进行标准化处理，可以在一定程度上缓解多重共线性问题。

深入探讨

不处理多重共线性的后果：

如果不处理多重共线性问题，回归模型可能会给出误导性的结果，使得我们无法准确判断哪些自变量对因变量有实际影响。模型的预测性能也会因此受到影响，导致在新数据上的泛化能力较差。

与单共线性的区别：

单共线性指的是一个自变量和因变量之间存在的线性相关性，而多重共线性是指多个自变量之间的高度相关性。多重共线性问题更为复杂，因为它涉及到多个自变量之间的关系，对模型的影响也更为显著。

防失联，进免费知识星球，直达算法金 AI 实验室 https://t.zsxq.com/ckSu3

更多内容，见免费知识星球

3. 什么是自相关性，自相关性对线性回归有什么影响？

定义和背景

自相关性指的是在时间序列数据或空间数据中，观测值之间存在相关性，即某个观测值与其前后的观测值之间存在一定的依赖关系。简单来说，就是某个时间点的值与其前后时间点的值之间存在统计相关性。

详细解答

自相关性的影响

1. 违反独立性假设：线性回归假设观测值之间是相互独立的，但自相关性意味着观测值之间存在依赖关系，这违反了线性回归模型的独立性假设。
2. 标准误差的低估：自相关性会导致残差之间不再独立，进而使得标准误差的估计值偏低。这会导致回归系数的显著性检验失效，即实际不显著的回归系数可能被误认为显著。
3. 模型的误导性结果：由于自相关性存在，线性回归模型可能会给出误导性的结果，使得模型的预测性能下降。模型可能无法准确捕捉数据中的真实模式。
4. 提高预测误差：自相关性会导致模型的预测误差增大，尤其是在对未来值进行预测时，模型可能会严重偏离真实值。

如何检测和处理自相关性

1. 自相关函数（ACF）和偏自相关函数（PACF）：通过绘制自相关函数（ACF）和偏自相关函数（PACF）图，可以直观地观察数据中的自相关性。
2. Durbin-Watson检验：Durbin-Watson统计量是检测自相关性的一种常用方法，其值在 0 到 4 之间，接近 2 表示没有自相关性，接近 0 表示正自相关，接近 4 表示负自相关。
3. 差分法：对时间序列数据进行差分处理，消除趋势和季节性成分，从而减小自相关性。
4. 加入滞后项：在模型中加入滞后项，即将前几期的观测值作为自变量，可以有效捕捉自相关性。

深入探讨

不处理自相关性的后果：

如果不处理自相关性问题，线性回归模型可能会给出误导性的结果，导致错误的决策。例如，在经济和金融数据分析中，忽视自相关性可能会导致对市场趋势和风险的误判。

与多重共线性的区别：

多重共线性是自变量之间的相关性，而自相关性是观测值之间的相关性。前者影响回归系数的稳定性和显著性检验，后者影响模型的假设检验和预测性能。

4. 什么是异方差性，如何检测和处理异方差性？

定义和背景

异方差性指的是在回归分析中，误差项的方差随着自变量或观测值的变化而变化。也就是说，误差项的方差不是恒定的，而是依赖于某些因素。这违反了线性回归模型的假设之一，即误差项的方差是恒定的（同方差性）。

详细解答

异方差性的影响

1. 参数估计的不准确：由于异方差性导致误差项的方差变化，回归系数的估计值可能会失真，使得模型的预测效果降低。
2. 标准误差的估计错误：异方差性会导致标准误差的估计值不准确，进而影响假设检验的结果。具体表现为置信区间和显著性检验的结果可能不可靠。
3. 模型的解释力下降：由于误差项的方差不恒定，模型对因变量的解释力会下降，使得解释变量对因变量的影响变得不清晰。

如何检测异方差性

1. 残差图：绘制标准化残差与拟合值的散点图。如果残差图呈现出某种系统性的图案（如漏斗形），则可能存在异方差性。
2. Breusch-Pagan检验：Breusch-Pagan检验是一种常用的检测异方差性的方法，通过对误差项的方差进行检验，判断是否存在异方差性。
3. White检验：White检验是一种更加通用的异方差性检验方法，适用于检测异方差性的多种情况。

如何处理异方差性

1. 对数变换或Box-Cox变换：对因变量或自变量进行对数变换或Box-Cox变换，可以减小或消除异方差性。
2. 加权最小二乘法（WLS）：通过为每个观测值分配不同的权重（通常权重与误差项的方差成反比），可以有效处理异方差性问题。
3. 稳健标准误差：使用稳健标准误差（如Heteroskedasticity-Consistent Standard Errors）可以调整标准误差的估计值，从而使得假设检验结果更可靠。

深入探讨

不处理异方差性的后果：

如果不处理异方差性问题，回归模型的估计值和假设检验结果可能会失真，从而影响决策的准确性。例如，在金融数据分析中，忽视异方差性可能导致对风险和收益的错误评估。

与其他回归问题的比较：

与多重共线性和自相关性不同，异方差性主要影响误差项的方差，而多重共线性和自相关性分别影响自变量之间的相关性和观测值之间的依赖关系。

防失联，进免费知识星球，直达算法金 AI 实验室

https://t.zsxq.com/ckSu3

免费知识星球，欢迎加入交流

5. 训练数据与测试数据分布不一致会带来什么问题，如何确保数据分布一致性？

定义和背景

在机器学习中，模型的训练过程使用训练数据，而其性能评估则依赖于测试数据。理想情况下，训练数据和测试数据应当来自同一个分布，即它们在特征和标签上的分布应当一致。然而，实际应用中，这种一致性可能因为各种原因（如数据收集方法、时间变化等）而被打破，这种现象被称为训练-测试分布不一致（Train-Test Distribution Mismatch）。

详细解答

分布不一致带来的问题

1. 模型泛化能力下降：如果训练数据和测试数据的分布不一致，模型在训练过程中学到的模式和规律可能无法在测试数据中有效应用，导致模型泛化能力下降，在实际应用中的表现不佳。
2. 过拟合或欠拟合风险增加：分布不一致可能导致模型过拟合于训练数据中的噪声和特定模式，而无法在测试数据上进行准确预测。或者，模型可能对训练数据中的特定模式学习不足，导致欠拟合。
3. 性能评估偏差：分布不一致会导致性能评估结果不可靠。模型在训练数据上的良好表现并不能代表其在实际应用中的表现，因为测试数据的分布不同于训练数据。
4. 误导性的特征重要性：当训练和测试数据分布不一致时，模型可能会错误地评估特征的重要性，导致在实际应用中依赖不重要或不相关的特征。

如何确保数据分布一致性

1. 数据收集的一致性：确保训练数据和测试数据的收集方法和条件尽可能一致。例如，在时间序列数据中，可以确保训练数据和测试数据来自相同的时间段或相同的市场条件。
2. 使用交叉验证：交叉验证是一种有效的评估方法，可以通过多次将数据分为训练集和测试集，确保模型在不同数据子集上的表现一致，从而减小分布不一致的影响。
3. 重采样技术：使用重采样技术（如上采样、下采样）来平衡训练数据和测试数据的分布。例如，对于分类问题，可以确保各类样本在训练集和测试集中的比例一致。
4. 归一化和标准化：对数据进行归一化和标准化处理，确保训练数据和测试数据在相同的尺度上，从而减小分布差异带来的影响。
5. 域自适应技术：当无法避免分布不一致时，可以使用域自适应技术（Domain Adaptation），通过对源域（训练数据）和目标域（测试数据）进行对齐，减小分布差异。

与其他数据问题的比较：

训练-测试分布不一致与多重共线性、自相关性和异方差性等问题不同，它主要影响模型的泛化能力和性能评估，而不是模型的内部结构和假设。

[ 抱个拳，总个结 ]

• 科研为国分忧，创新与民造福 -

日更时间紧任务急，难免有疏漏之处，还请大侠海涵内容仅供学习交流之用，部分素材来自网络，侵联删

[ 算法金，碎碎念 ]

全网同名，日更万日，让更多人享受智能乐趣

如果觉得内容有价值，烦请大侠多多 分享、在看、点赞，助力算法金又猛又持久、很黄很 BL 的日更下去；

同时邀请大侠 关注、星标 算法金，围观日更万日，助你功力大增、笑傲江湖