基于贝叶斯优化的自适应马尔科夫链蒙特卡洛(Adaptive-MCMC)算法matlab仿真

目录

1.程序功能描述

2.测试软件版本以及运行结果展示

3.核心程序

4.本算法原理

[4.1 自适应MCMC](#4.1 自适应MCMC)

[4.2 贝叶斯优化](#4.2 贝叶斯优化)

[4.3 基于贝叶斯优化的Adaptive-MCMC算法](#4.3 基于贝叶斯优化的Adaptive-MCMC算法)

[4.4 Kawasaki sampler，IMExpert，IMUnif以及IMBayesOpt](#4.4 Kawasaki sampler，IMExpert，IMUnif以及IMBayesOpt)

5.完整程序

---

1.程序功能描述

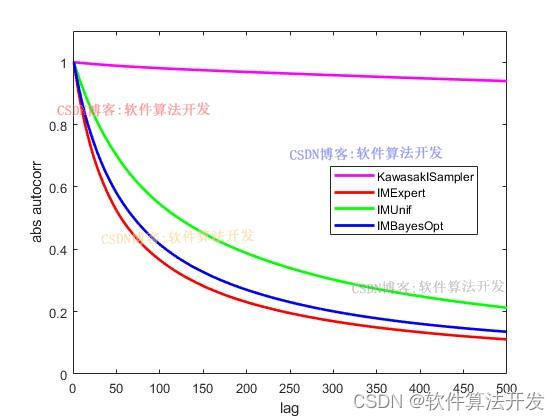
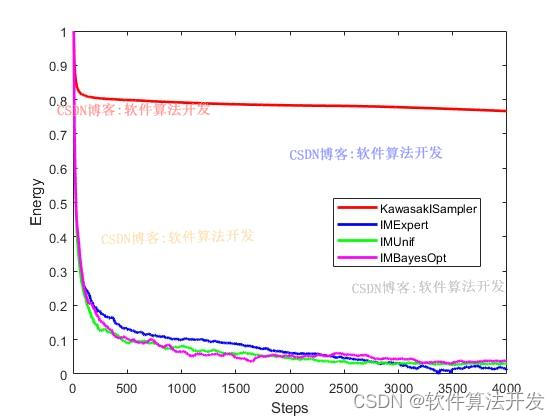
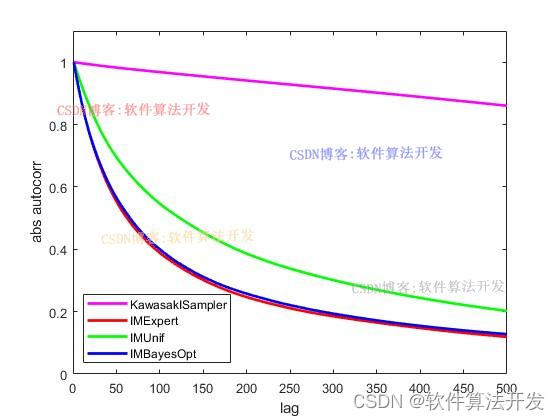
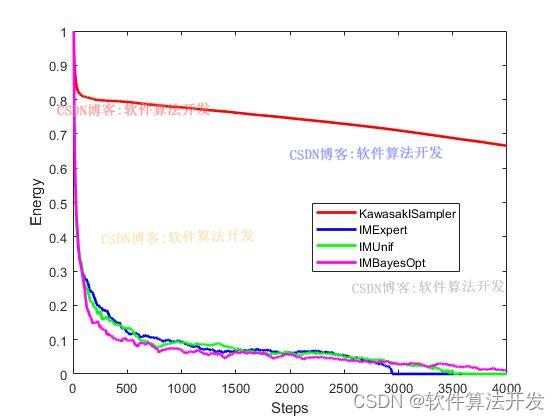
基于贝叶斯优化的自适应马尔科夫链蒙特卡洛(Adaptive-MCMC)算法matlab仿真.对比Kawasaki sampler，IMExpert，IMUnif以及IMBayesOpt。

2.测试软件版本以及运行结果展示

MATLAB2022A版本运行

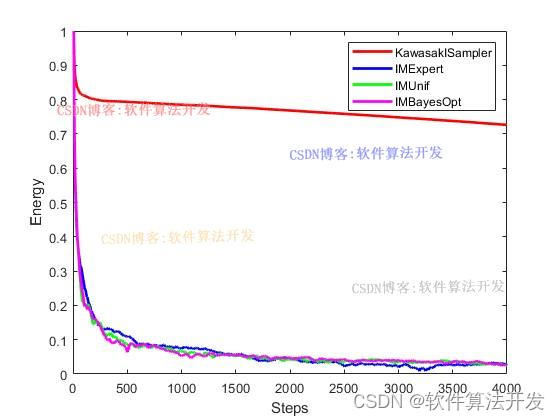
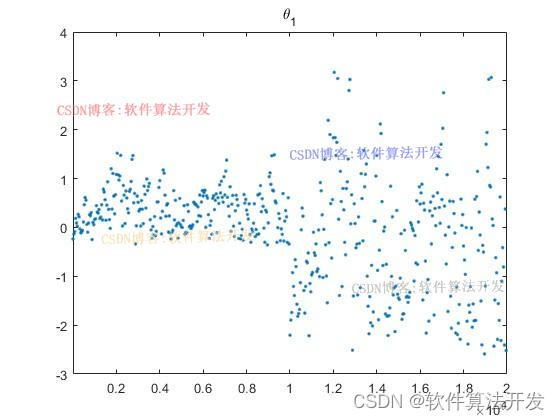
（完整程序运行后无水印）

3.核心程序

......................................................................

% 以下部分（IMExpert, IMUnif, IMBayesOpt）与KawasakISampler类似，
%IMBayesOpt
r     = 1;
k     = 50;
for i = 1:n
    x0(i) = randn*i;
end
x     = x0*exp(-beta*mean(x0));
delta = std(x);
lags  = [0:600];
for lag = lags
    lag
    tmps = [];
    for t = 1:n-lag
        tmps(t) = (x(t)-mean(x))*(x(t+lag)-mean(x)); 
    end
    r(lag+1) = 1/((n-lag)*delta^2) * sum((tmps)); 
    %mean ACFs
    if lag<=max(lags)
       r1(lag+1) = mean(r(1:lag+1)); 
    else
       r1(lag+1) = mean(r(lag+1-max(lags):lag+1));  
    end
    if lag<=max(lags)
       r2(lag+1) = mean(r1(1:lag+1)); 
    else
       r2(lag+1) = mean(r1(lag+1-max(lags):lag+1));  
    end
end

r3 = r2(101-k:601-k);
r3 = r3/max(r3);
plot(r3,'b','linewidth',2);
hold on


xlabel('lag');
ylabel('abs autocorr');
axis([0,500,0,1.1]);
legend('KawasakISampler','IMExpert','IMUnif','IMBayesOpt');
16_042m

4.本算法原理

基于贝叶斯优化的自适应马尔科夫链蒙特卡洛（Adaptive Markov Chain Monte Carlo, Adaptive-MCMC）算法是一种结合了贝叶斯优化思想与MCMC抽样技术的高级采样方法，旨在高效地探索复杂的概率分布，特别是那些具有多模态、强相关性或非凸性的分布。这种算法的核心在于利用历史采样信息自适应地调整采样策略，以提高样本的效率和对后验分布的探索能力。

MCMC算法是一种用于从复杂分布中抽取样本的数值方法，特别是当直接抽样不可行时。其基本思想是构造一个马尔科夫链，其平稳分布正好是感兴趣的分布p(x)。给定当前状态xt​，下一个状态xt+1​的转移遵循转移概率T(xt+1​∣xt​)，且满足细致平衡条件：

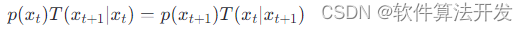
4.1 自适应MCMC

自适应MCMC算法通过在线学习，动态调整MCMC的参数（如提议分布的参数），以期在抽样过程中不断优化算法性能。这要求算法设计既要保证时间序列的马尔科夫链仍然是ergodic（遍历的），同时又要尽可能快地收敛到目标分布。

4.2 贝叶斯优化

贝叶斯优化是一种全局优化方法，它利用先验知识和观测数据，通过贝叶斯推理不断更新目标函数的后验分布，进而指导下一步的探索和利用。核心在于建立一个代理模型（通常是高斯过程）来近似未知的目标函数，并使用采集函数（如期望改善（EI）、上限置信区间（UCB）等）来确定最有希望的下一个采样点。

4.3 基于贝叶斯优化的Adaptive-MCMC算法

结合上述两种方法，基于贝叶斯优化的Adaptive-MCMC算法通常涉及以下几个关键步骤：

1. 构建目标函数：将MCMC算法的性能度量（如有效样本大小ESS、自相关长度等）作为优化目标。目标是最大化这些度量，从而提高采样效率。

2. 代理模型：使用高斯过程（Gaussian Process, GP）或其他机器学习模型作为目标函数的代理。代理模型基于已有的采样点和对应的性能度量值来预测新的参数设置下的性能。

3. 采集函数：基于代理模型的预测和不确定性，选择一个采集函数来指导参数的更新。例如，期望改善(EI)鼓励探索未采样区域和利用已知的良好区域。

4. 参数调整：依据采集函数的建议，调整MCMC算法的参数（如提议步长、接受率等），然后执行MCMC抽样。

5. 反馈循环：将新抽样点的性能度量反馈给代理模型，更新模型，并重复步骤3-4，形成闭环自适应过程。

4.4 Kawasaki sampler，IMExpert，IMUnif以及IMBayesOpt

5.完整程序

VVV