决策树(Decision Tree)
决策树算法是一种常用的机器学习算法,属于监督学习范畴。它可以用于分类和回归任务,具有易于理解和解释的特点。决策树通过递归将数据分割成更小的子集,构建一个树形结构,其中每个节点代表一个特征的测试,分支代表测试结果,叶子节点代表最终的分类或回归结果。
1. 基本概念
-
根节点(Root Node):树的最顶端节点,包含所有数据样本。
-
内部节点(Internal Nodes):每个内部节点表示一个特征的测试,根据测试结果将数据分成两个或多个子集。
-
叶子节点(Leaf Nodes):树的末端节点,表示最终的分类或回归结果。
-
分支(Branches):从一个节点到下一个节点的路径,代表特征测试的结果。
2. 构建过程
构建决策树的过程涉及以下几个步骤:
-
选择最优特征:在每个节点选择一个特征来分割数据。选择的标准通常是信息增益、信息增益率或基尼指数等。
-
数据分割:根据选择的特征和阈值,将数据分割成子集。
-
递归分割:对每个子集重复上述步骤,直到满足停止条件,如所有数据属于同一类或达到最大树深度。
-
构建树形结构:将上述分割过程形成树形结构,根节点和内部节点代表特征测试,叶子节点代表最终预测。
3. 特征选择标准
-
信息增益(Information Gain):衡量特征在分割数据后信息熵的减少量。选择信息增益最大的特征进行分割。
-
基尼指数(Gini Index):用于衡量数据集的不纯度。选择基尼指数最小的特征进行分割。
-
信息增益率(Gain Ratio):信息增益的一种改进,考虑了特征取值的不同数量,选择信息增益率最大的特征进行分割。
4. 优点和缺点
优点:
-
易于理解和解释,适合展示和解释复杂决策
-
可以处理数值型和类别型数据
-
不需要太多的数据预处理(如标准化、归一化)
缺点:
-
容易过拟合,特别是当树很深时
-
对于有噪声的数据敏感,可能导致不稳定的树结构
-
决策树可能偏向于那些具有较多类别的特征
5. 应用
决策树在很多领域都有广泛的应用,例如:
-
医疗诊断:根据病人的症状和检查结果,预测疾病
-
金融:信用评分、欺诈检测
-
市场营销:客户分类、行为预测
-
制造业:质量控制、故障诊断
6. 示例
一个简单的决策树分类问题示例是预测某个学生是否会通过考试,特征可以包括学习时间、上课出勤率、是否完成作业等。决策树会根据这些特征逐步分割数据,最终在叶子节点给出"通过"或"不通过"的预测。
是否完成作业?
/ \
是 否
/ \
学习时间 > 2小时? 不通过
/ \
是 否
/ \
通过 不通过通过这个例子可以看到,决策树通过逐层分割特征,将数据分成不同的子集,最终在叶子节点给出预测结果。以下是一个简单的代码示例:
import matplotlib.pyplot as plt # 用于绘图
from sklearn.datasets import load_iris # 用于加载Iris数据集
from sklearn.tree import DecisionTreeClassifier, plot_tree # 前者用于创建决策树分类器,后者用于可视化决策树
from sklearn.model_selection import train_test_split # 用于将数据集分为训练集和测试集
from sklearn.metrics import accuracy_score # 用于计算预测的准确率
# 加载Iris数据集
iris = load_iris() # 调用load_iris函数加载Iris数据集,并将其存储在变量iris中
X = iris.data # 将Iris数据集中的特征数据存储在变量X中
y = iris.target # 将Iris数据集中的目标标签存储在变量y中
# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # 将数据集X和y分为训练集和测试集,test_size=0.3表示30%的数据用作测试集,random_state=42设置随机种子以保证结果可重复
# 创建决策树分类器
clf = DecisionTreeClassifier(random_state=42) # 创建一个DecisionTreeClassifier对象,random_state=42设置随机种子以保证结果可重复
clf.fit(X_train, y_train) # 使用训练集数据X_train和y_train训练决策树分类器
# 预测测试集
y_pred = clf.predict(X_test) # 使用训练好的决策树分类器对测试集X_test进行预测,并将预测结果存储在变量y_pred中
# 计算准确率
accuracy = accuracy_score(y_test, y_pred) #调用accuracy_score函数,计算预测结果y_pred与真实标签y_test的准确率,并将结果存储在变量accuracy中
print(f'Accuracy: {accuracy:.2f}')
# 可视化决策树
plt.figure(figsize=(20,10)) # 创建一个新的图形,并设置图形的尺寸为20x10英寸
plot_tree(clf, filled=True, feature_names=iris.feature_names, class_names=iris.target_names.tolist(), rounded=True) # 调用plot_tree函数绘制决策树,节点用颜色填充,颜色深浅表示样本数量,rounded=True:使用圆角矩形表示节点
plt.show()可视化结果:
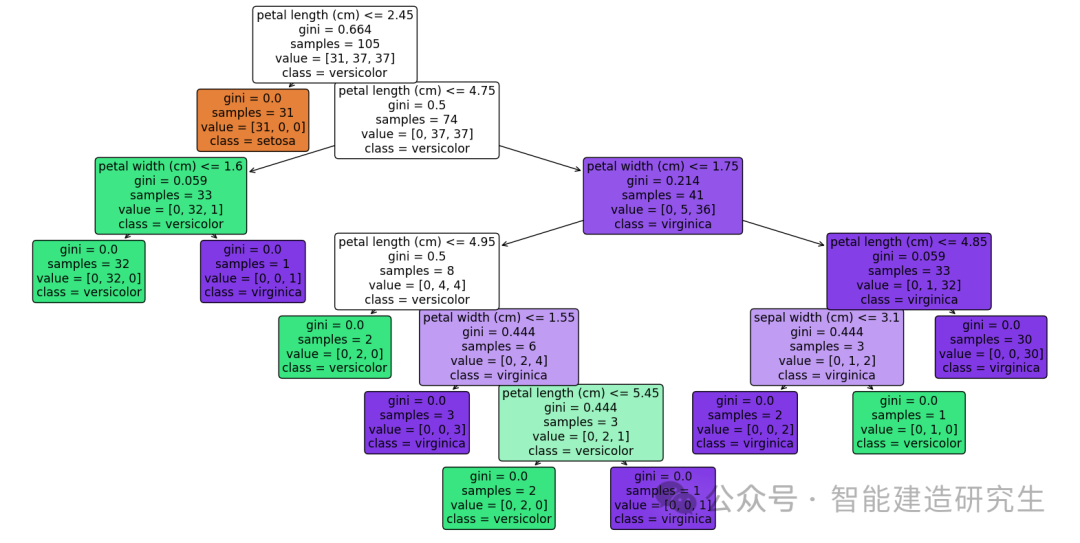
在决策树的可视化结果中,每个节点包含了多个信息。这些信息帮助我们理解每个节点的决策过程。
以下是对每个节点中数据的解释:
1.Feature and Threshold(特征和阈值):
-
每个内部节点(非叶子节点)显示用于分割数据的特征和阈值。
-
例如,如果节点显示
petal length (cm) <= 2.45,表示根据petal length (cm)特征,值小于等于 2.45 的样本被分到左子树,值大于 2.45 的样本被分到右子树。
2.Gini(基尼系数):
- 基尼系数用于衡量数据集的不纯度。基尼系数越小,数据集越纯(即单一类别的样本比例越高)。计算公式为其中 ( pi ) 是第 ( i ) 类的样本比例。
3.Samples(样本数量):
- 每个节点中样本的总数量。例如,如果节点显示
samples = 50,表示该节点包含50个样本。
4.Value(类别分布):
-
每个节点中不同类别样本的数量。
-
例如,如果节点显示
value = [10, 40],表示该节点包含10个属于第一类的样本和40个属于第二类的样本。
5.Class(类别):
- 每个节点中占多数的类别(仅叶子节点)。例如,如果节点显示
class = versicolor,表示该节点的多数类别是versicolor。
假设我们有如下的决策树节点可视化结果:
petal length (cm) <= 2.45
gini = 0.5
samples = 100
value = [50, 50]
class = setosa这个节点的信息解释如下:
-
petal length (cm) <= 2.45:使用花瓣长度作为特征,阈值是2.45。花瓣长度小于等于2.45的样本会被分到左子树,大于2.45的样本会被分到右子树。
-
gini = 0.5:基尼系数为0.5,表示数据集的不纯度较高(这通常是根节点或接近根节点的情况)。
-
samples = 100:该节点包含100个样本。
-
value = [50, 50]:这100个样本中,有50个属于第一类(例如,
setosa),50个属于第二类。 -
class = setosa :在这个节点中,占多数的类别是
setosa(但在这种情况下,实际上类别是平分的)。
这些信息帮助我们理解模型如何基于特征一步步做出决策。以上内容总结自网络,如有帮助欢迎转发,我们下次再见!