Deep-Learning-Interview-Book/docs/深度学习.md at master · amusi/Deep-Learning-Interview-Book · GitHub
网上相关总结:
Epoch
- Epoch 是指完成一次完整的数据集训练的过程。
- 比如,有一个数据集有1000个样本,当网络用这些样本训练一次后,这就是一个epoch。
Iteration
- Iteration 是指在一个epoch中,使用一个batch进行训练的次数。
- 如果你的数据集有1000个样本,batch size是100,那么一个epoch就会有10次iteration(1000/100=10)。
Batch Size
- Batch Size 是指每次iteration中用于训练的样本数量。
- 如果你的batch size是100,每次训练就使用100个样本。
反向传播(BP)推导
假设我们有一个简单的三层神经网络(输入层、隐藏层和输出层):
- 输入层: xxx
- 隐藏层: hhh
- 输出层: yyy
前向传播
-
输入到隐藏层: h=f(Wxhx+bh)h = f(W_{xh} x + b_h)h=f(Wxhx+bh) 其中 WxhW_{xh}Wxh 是输入到隐藏层的权重矩阵,bhb_hbh 是隐藏层的偏置向量,fff 是激活函数。
-
隐藏层到输出层: y^=g(Whyh+by)\hat{y} = g(W_{hy} h + b_y)y^=g(Whyh+by) 其中 WhyW_{hy}Why 是隐藏层到输出层的权重矩阵,byb_yby 是输出层的偏置向量,ggg 是输出层的激活函数,通常在分类问题中是softmax函数。
损失函数
假设我们使用均方误差损失函数: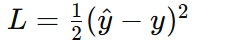
其中 yyy 是实际输出,y^\hat{y}y^ 是预测输出。
反向传播
我们需要计算损失 LLL 对每个权重和偏置的梯度,然后更新这些参数。我们从输出层开始,逐层向后推导。
-
输出层梯度 :
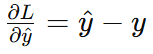
-
隐藏层到输出层权重梯度 :
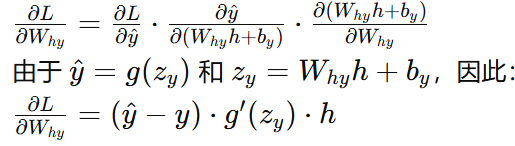
-
隐藏层到输出层偏置梯度 :
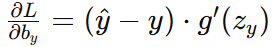
-
隐藏层误差 :
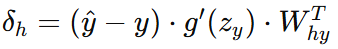
-
输入层到隐藏层权重梯度 :
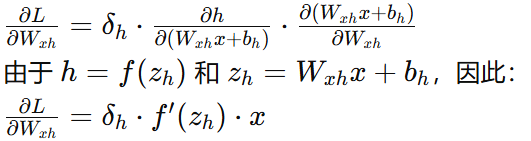
-
输入层到隐藏层偏置梯度 :

参数更新
使用梯度下降法更新权重和偏置:
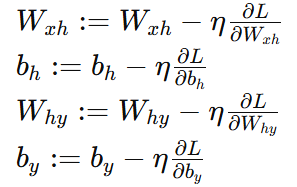
其中 η 是学习率。
深度神经网络(DNN)反向传播算法(BP) - 刘建平Pinard - 博客园 (cnblogs.com)

感受野计算
如何计算感受野(Receptive Field)------原理 - 知乎 (zhihu.com)
池化
1. 池化的作用
池化的主要作用有两个:
- 降低计算复杂度:通过减少特征图的尺寸,减少后续卷积层和全连接层的计算量。
- 减小过拟合:通过降低特征图的分辨率,可以使模型更具鲁棒性,对输入数据的小变化不那么敏感。
2. 池化类型
池化操作通常有两种类型:
- 最大池化(Max Pooling):从池化窗口中选择最大值。
- 平均池化(Average Pooling):从池化窗口中选择平均值。
池化(Pooling)的种类与具体用法------基于Pytorch-CSDN博客
一图读懂-神经网络14种池化Pooling原理和可视化(MAX,AVE,SUM,MIX,SOFT,ROI,CROW,RMAC )_图池化-CSDN博客
卷积神经网络(CNN)反向传播算法 - 刘建平Pinard - 博客园 (cnblogs.com)
Sobel边缘检测
是图像处理中常用的技术,它使用卷积核(滤波器)来突出图像中的边缘。Sobel算子通过计算图像灰度值的梯度来检测边缘。
1. Sobel算子
Sobel算子有两个卷积核,一个用于检测水平方向的边缘,另一个用于检测垂直方向的边缘。
水平Sobel卷积核(Gx)
diff
复制代码
-1 0 1 -2 0 2 -1 0 1
垂直Sobel卷积核(Gy)
diff
复制代码
-1 -2 -1 0 0 0 1 2 1
2. Sobel卷积操作
通过将这两个卷积核分别与图像进行卷积操作,可以得到图像在水平方向和垂直方向上的梯度图。
卷积计算过程
假设有一个3x3的图像块:
css
复制代码
a b c d e f g h i
水平方向的梯度计算(Gx):
css
复制代码
Gx = (c + 2f + i) - (a + 2d + g)
垂直方向的梯度计算(Gy):
css
复制代码
Gy = (g + 2h + i) - (a + 2b + c)
3. 组合梯度
最终的梯度强度可以通过组合Gx和Gy计算得到:
scss
复制代码
G = sqrt(Gx^2 + Gy^2)
梯度计算
通过这些卷积核,我们可以计算图像在水平方向和垂直方向的梯度。梯度表示图像灰度值的变化速率,变化速率大的地方就是边缘。具体来说:
- 水平方向梯度(Gx):表示图像从左到右的变化。如果有明显的水平边缘,Gx会有大的值。
- 垂直方向梯度(Gy):表示图像从上到下的变化。如果有明显的垂直边缘,Gy会有大的值。
4. 组合梯度
最终,通过组合水平方向和垂直方向的梯度(通常使用欧几里得距离),我们可以得到图像的梯度强度:
计算力(flops)和参数(parameters)数量
(31 封私信 / 80 条消息) CNN 模型所需的计算力(flops)和参数(parameters)数量是怎么计算的? - 知乎 (zhihu.com)


参数共享的卷积环节



不可导的激活函数如何处理



BN
BatchNormalization、LayerNormalization、InstanceNorm、GroupNorm、SwitchableNorm总结_四维layernormal-CSDN博客
Batch Normalization原理与实战 - 知乎 (zhihu.com)
Normalization操作我们虽然缓解了ICS问题 ,让每一层网络的输入数据分布都变得稳定 ,但却导致了数据表达能力的缺失 。BN又引入了两个可学习(learnable)的参数 𝛾 与 𝛽 。这两个参数的引入是为了恢复数据本身的表达能力,对规范化后的数据进行线性变换

重点最后一句





感受野计算
卷积神经网络物体检测之感受野大小计算 - machineLearning - 博客园 (cnblogs.com)


资源 | 从ReLU到Sinc,26种神经网络激活函数可视化 (qq.com)
非线性激活函数的线性区域


从 SGD 到 Adam ------ 深度学习优化算法概览(一) - 知乎 (zhihu.com)
一个框架看懂优化算法之异同 SGD/AdaGrad/Adam - 知乎 (zhihu.com)
指数移动平均公式
EMA指数滑动平均(Exponential Moving Average)-CSDN博客
动量梯度下降法(Momentum)
Adagrad
RMSprop
Adam
Adam那么棒,为什么还对SGD念念不忘 (2)------ Adam的两宗罪 - 知乎 (zhihu.com)
dropout
深度学习-Dropout详解_深度学习dropout-CSDN博客
Dropout的深入理解(基础介绍、模型描述、原理深入、代码实现以及变种)-CSDN博客
一文看尽12种Dropout及其变体-腾讯云开发者社区-腾讯云 (tencent.com)
Pytorch------dropout的理解和使用 - Circle_Wang - 博客园 (cnblogs.com)
1x1卷积
(31 封私信 / 80 条消息) 卷积神经网络中用1*1 卷积有什么作用或者好处呢? - 知乎 (zhihu.com)
深度学习笔记(六):1x1卷积核的作用归纳和实例分析_1x1卷积降维-CSDN博客
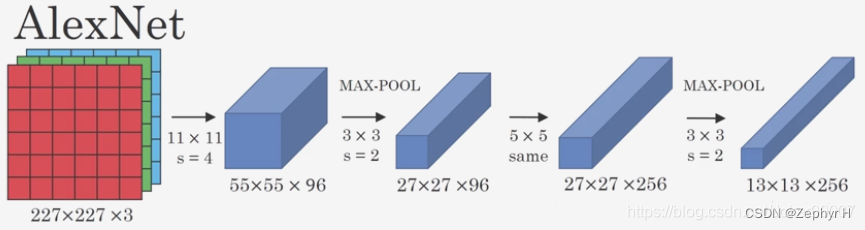



AlexNet网络结构详解(含各层维度大小计算过程)与PyTorch实现-CSDN博客
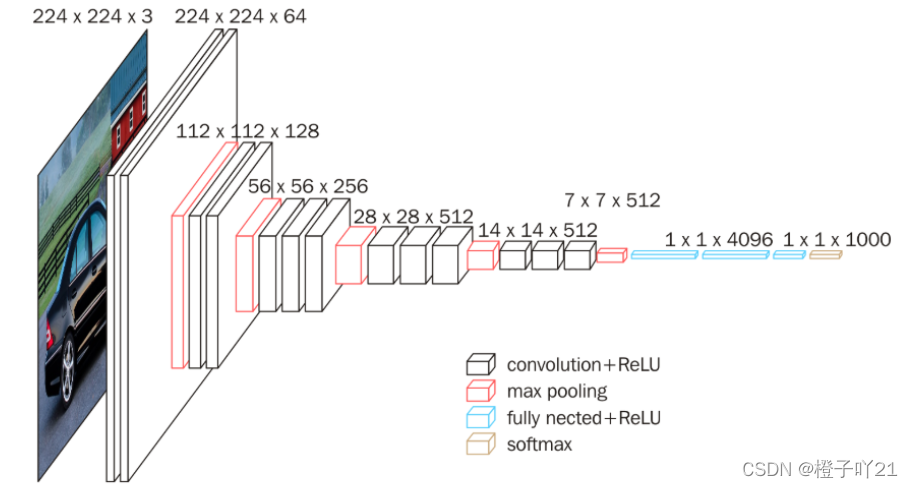

3乘3卷积代替5乘5卷积
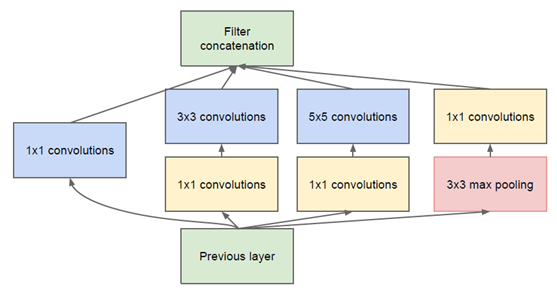
经典卷积神经网络算法(4):GoogLeNet - 奥辰 - 博客园 (cnblogs.com)
1x1卷积降维再接3x3卷积
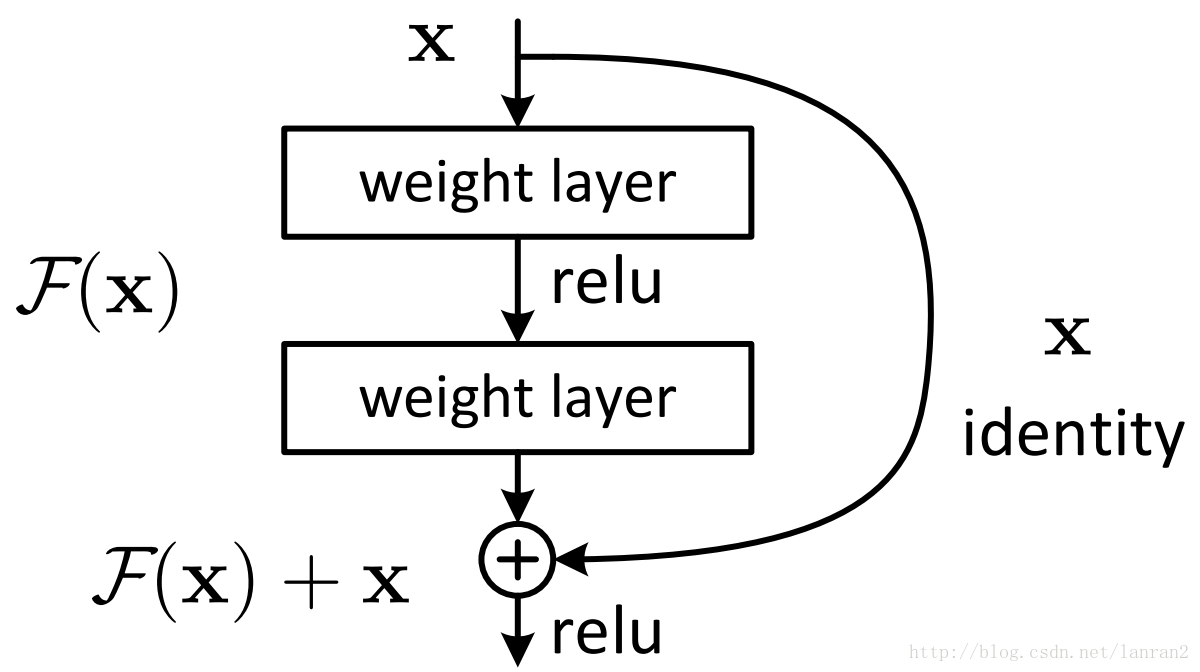
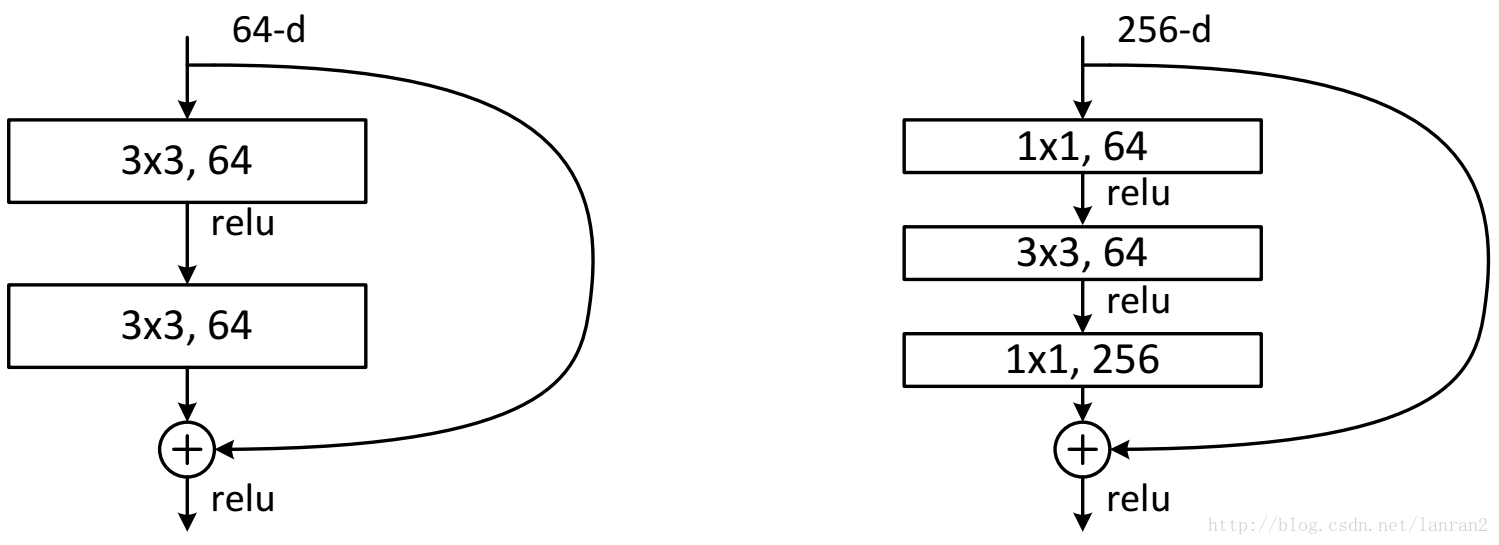
resnet
两种ResNet设计
channel不同怎么相加
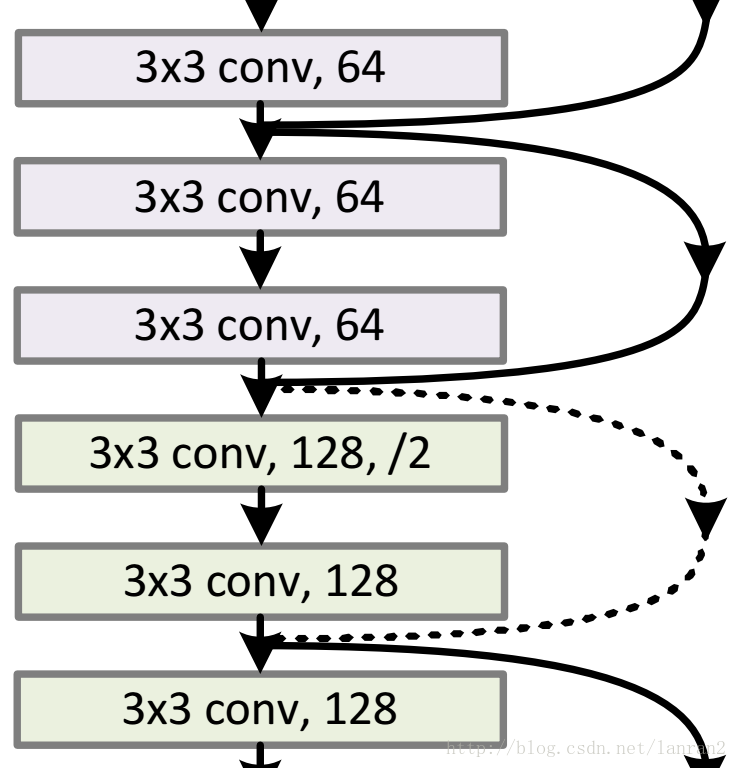 通过卷积调整
通过卷积调整


(31 封私信 / 80 条消息) resnet(残差网络)的F(x)究竟长什么样子? - 知乎 (zhihu.com)

(31 封私信 / 80 条消息) Resnet到底在解决一个什么问题呢? - 知乎 (zhihu.com)

残差连接使梯度稳定


ResNet中的恒等映射是一种直接将输入添加到输出的操作方式,确保了信息和梯度可以稳定地传递。它通过保持梯度的稳定性,防止了梯度消失和爆炸问题,从而使得训练非常深的网络成为可能。

(31 封私信 / 80 条消息) ResNet为什么不用Dropout? - 知乎 (zhihu.com)
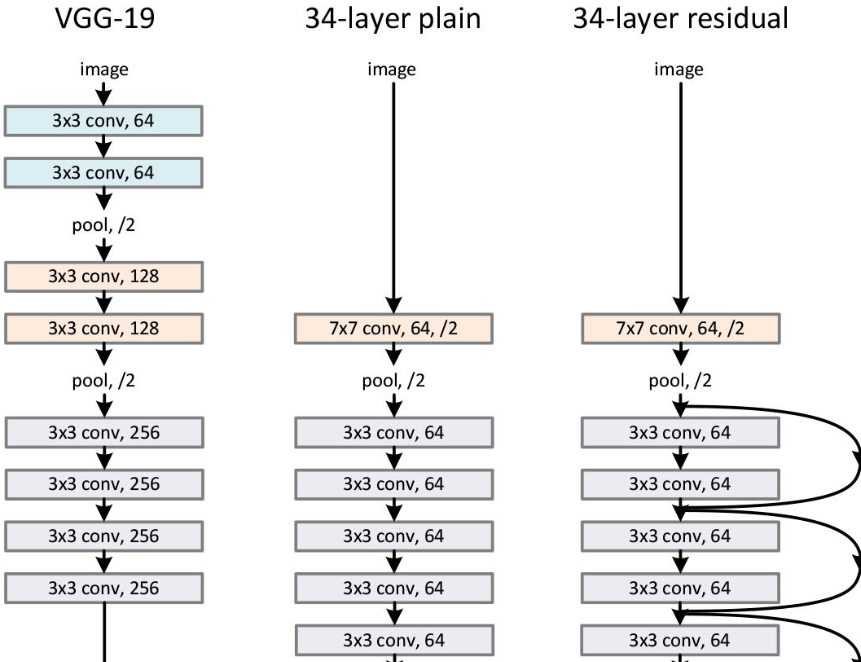

人工智能 - [ResNet系] 002 ResNet-v2 - G时区@深度学习 - SegmentFault 思否
yolo系列
YOLO系列算法全家桶------YOLOv1-YOLOv9详细介绍 !!-CSDN博客
【YOLO系列】YOLOv1论文超详细解读(翻译 +学习笔记)_yolo论文-CSDN博客
YOLO系列算法精讲:从yolov1至yolov8的进阶之路(2万字超全整理)-CSDN博客
NMS
v2引入anchor
分割
计算机视觉---浅谈语义分割、实例分割及全景分割任务 (深度学习/图像处理/计算机视觉)_全景分割和实例分割-CSDN博客
【计算机视觉】最全语义分割模型总结(从FCN到deeplabv3+)-CSDN博客
目标检测与YOLO(2) + 语义分割(FCN)_yolo模型和fcn-CSDN博客
【yolov8系列】yolov8的目标检测、实例分割、关节点估计的原理解析-CSDN博客
yolo实现实例分割和关键点预测,都是在head部分增加新的检测头实现



Bounding-box regression详解(边框回归)_bbox regression-CSDN博客

反卷积(Deconvolution)、上采样(UNSampling)与上池化(UnPooling)_反卷积和上采样-CSDN博客
形象解释: