潜在空间可视化（Latent space visualization）

在"深度学习"系列中，我们不会看到如何使用深度学习来解决端到端的复杂问题，就像我们在《A.I. Odyssey》中所做的那样。我们更愿意看看不同的技术，以及一些示例和应用程序。

1、引言

上次（Autoencoders - Deep Learning bits #1），我们已经了解了什么是自动编码器（autoencoders），以及它们时如何工作的。今天，我们将看到它们如何以一些非常酷的方式帮助我们将数据可视化。为此，我们将使用**卷积自编码器架构（Convolutional AutoEncoder architecture，CAE）**处理图像。

① 什么是潜在空间？

自动编码器由两个组件组成，这里有一个快速提示。编码器（encoder）将来自高维输入的数据带到瓶颈层（bottleneck layer），那里的神经元数量最少。然后，解码器接受这个编码输入并将其转换回原始输入形状---在我们的例子中是图像。潜在空间是数据位于瓶颈层的空间。

卷积编码器-解码器架构

潜在空间包含图像的压缩表示（compressed representation），这是解码器允许使用的唯一信息，以尽可能忠实地重建输入。为了表现良好，网络必须学会在瓶颈层中提取最相关的特征。

让我们看看我们能做什么！

2、数据

我们将研究可能是最著名的计算机视觉手写数字的MNIST数据集。为了多样性，我通常更喜欢使用不太传统的数据集，但MNIST对于我们今天要做的事情来说真的很方便。

注意：尽管MNIST可视化在互联网上很常见，但本文中的图像是100%由代码生成的，因此您可以将这些技术用于您自己的模型。

MNIST是一个有28×28个手写数字图像的标记数据集。

3、基线---自动编码器的性能

为了理解编码器能够从输入中提取什么样的特征，我们可以首先看一下重建的图像。

注意：在这篇文章中，瓶颈层只有32个单元，这是一些非常非常残酷的维数缩减。如果它是一张图像，它甚至不会是6×6像素。

每个数字都显示在其模糊的重建旁边。

我们可以看到，自动编码器成功地重建了数字。重建是模糊的，因为输入在瓶颈层被压缩。我们需要查看验证样本的原因是为了确保我们没有过度拟合训练集。

这是训练过程动画：

每一步重建训练样本（左）和验证样本（右）。

4、t-SNE 可视化

① 什么是t-SNE？

在处理数据集时，我们要做的第一件事是一种有意义的方式将数据可视化。在我们的例子中，图像（或像素）空间有784维（28×28×1），我们显然无法绘制它。我们面临的挑战是将所有这些维度压缩成我们可以掌握的2D或3D形式。

这就是t-SNE，一种将高维空间映射到2D或3D空间的算法，同时试图保持点之间距离不变。我们将使用这种技术来绘制我们数据集的嵌入，首先直接从图像空间，然后从较小的潜在空间。

注意：t-SNE比它的近亲PCA和ICA更适合于可视化。

② 投影像素空间（Projecting the pixel space）

让我们从绘制数据集（来自图像空间）的t-SNE嵌入开始，看看它是什么样子。

来自验证集的图像空间表示的t-SNE投影。

我们已经可以看到一些数字大致聚集在一起。这是因为数据集非常简单，我们可以使用简单的启发式像素对样本进行分类。看看数字8、5、7和3是如何没有聚类的，这是因为它们都是由相同的像素组成的，只有微小的变化才能区分它们。

对于更复杂的数据，如RGB图像，唯一的聚类将是相同颜色的图像。

③ 投影潜在空间（Projecting the latent space）

我们知道潜在空间包含了一个比像素空间更简单的图像表示，所以我们可以希望t-SNE能给出一个有趣的潜在空间的二维投影。

来自验证集的潜在空间表示的t-SNE投影。

虽然不完美，但投影显示了更密集的星团。这表明，在潜在空间中，相同的数字彼此接近。我们可以看到，数字8、7、5和3现在更容易区分，并且出现在小集群中。

5、插值（Interpolation）

现在我们知道了模型能够提取的详细程度，我们可以探测潜在空间的结构。为了做到这一点，我们将比较插值在图像空间和潜在空间中的表现。

① 在图像空间中的线性插值（Linear interpolation in image space）

我们首先从数据集中获取两幅图像，并在它们之间进行线性插值。这有效地将图像以一种幽灵般的方式混合在一起。

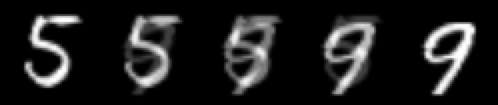
像素空间插值。

造成这种混乱过渡的原因是像素空间本身的结构。在图像空间中，从一个图像平滑地转换到另一个图像是不可能的。这就是为什么把空杯子的图像和满杯子的图像混合在一起不会得到半满杯子的图像的原因。

② 在潜在空间中的线性插值（Linear interpolation in latent space）

现在，我们对潜在空间做同样的处理。我们取相同的起始和结束图像，并将它们输入编码器以获得它们的潜在空间表示。然后我们在两个潜在向量之间进行插值，并将这些输入到解码器中。

潜在空间插值。

结果更有说服力。我们可以清楚地看到形状从一个数字慢慢地转变为另一个数字，而不是两个数字的褪色覆盖。这显示了潜在空间对图像结构的理解程度。

这是两个空间的插值动画：

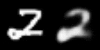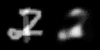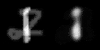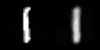
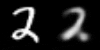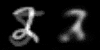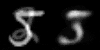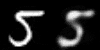
图像空间（左）和潜在空间（右）的线性插值。

6、更多技术和样例

① 插值样例

在更丰富的数据集和更好的模型上，我们可以得到令人难以置信的视觉效果。

3-way潜在空间插值的人脸。

3D形状的插值。

② 潜在空间算术（arithmetics）

我们也可以在潜在空间中做算术。这意味着我们可以添加或减去潜在空间表示，而不是差值。

举个例子，man with glasses - man without glasses + woman without galsses = woman with glasses。这种方法会产生令人兴奋的效果。

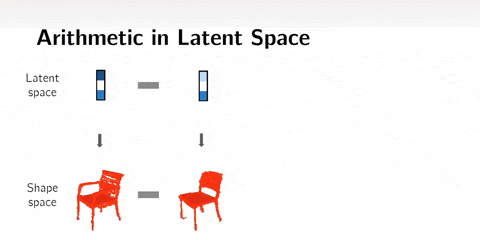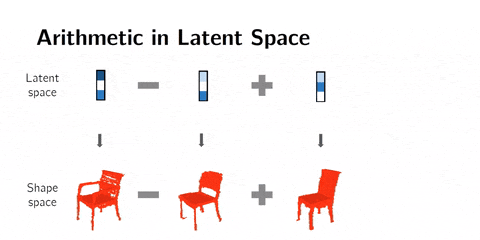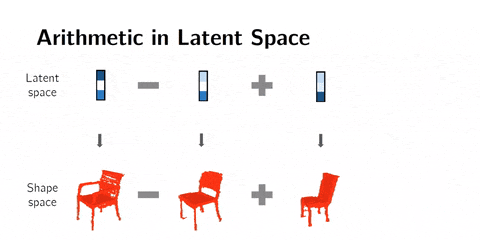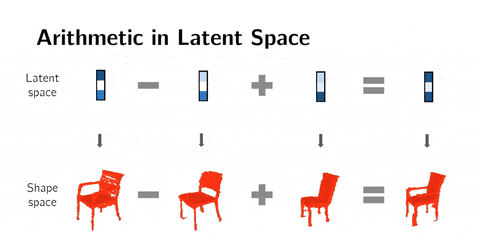
3D形状的算术。

注意：我在代码中放置了一个函数，但是它在MNIST上看起来很糟糕。

7、总结

在这篇文章中，我们已经看到了几种技术来可视化嵌入在自编码器神经网络潜在空间中的学习特征。这些可视化有助于理解网络正在学习什么。在此基础上，我们可以利用潜在空间进行集群、压缩和许多其他应用程序。

你可以试试那边的代码：

一个卷积自编码器的潜在空间的可视化技术：https://github.com/despoisj/LatentSpaceVisualization?ref=hackernoon.com

8、名词解释

① 什么叫端到端的复杂问题（complex problems end-to-end）？

"端到端的复杂问题"通常指的是那些需要多个步骤或组件协同工作才能解决的问题。在深度学习领域，这可能意味着一个系统需要从原始数据直接学习到最终输出，而不需要人为地进行中间步骤的干预或特征工程。这类问题通常具有以下特点：

数据驱动：问题解决过程完全依赖于数据输入，系统通过学习数据模式来做出决策。
自动化：系统能够自动地从数据中学习并进行预测或决策，无需人为设置特定的规则或参数。
多步骤处理：问题可能包含多个阶段，如特征提取、模式识别、决策制定等，这些阶段在系统内部自动串联起来。
高复杂性：问题本身可能非常复杂，涉及多种变量和不确定性，需要高级的算法和模型来处理。

例如，在《A.I. Odyssey》中，可能描述了一个深度学习系统如何从原始图像数据中自动学习并识别出图像中的对象，这个过程包括了图像预处理、特征提取、分类等多个步骤，但整个过程是自动完成的，不需要人为干预。

与之相对的，是一些更简单的问题，可能只需要单一的模型或算法就能解决，或者需要人为地进行一些预处理或后处理步骤。在深度学习的"系列"中，可能更倾向于展示不同的技术、算法和它们在特定问题上的应用，而不是深入探讨如何构建一个完整的端到端系统来解决极其复杂的问题。

② 简单了解t-SNE

t-SNE，降维方法之一。降维在机器学习中非常重要。这是因为如果使用高维数据创建模型，则很容易欠拟合。换句话说，有太多无用的数据需要学习。可以通过从各种数据中仅选择最重要的数据在模型中使用它，也可以使用多个数据创建新数据并使其低维。无论如何，有必要将此类高维数据转换为低维数据。这称为降维。还有其他方法可以创建要素，例如"特征消除"和"特征选择"。降维方法有两种类型：线性方法（主成分分析法PCA，独立成分分析法，线性判别分析法等）和非线性方法（歧管，自动编码器等）。t-SNE是非线性方法之一。

它是从SNE（随机邻居嵌入）演变为t-SNE（t分布随机邻居嵌入），然后发展到UMAP（均匀流形近似和投影）。

t-SNE是由t和SNE组成，t分布和随机近邻嵌入（Stochastic Neighbor Embedding）。
t-SNE是一种可视化工具，将高维数据降到2-3维，然后画成图。
t-SNE是目前效果最好的数据降维和可视化方法。
t-SNE的缺点是：占用内存大，运行时间长。

t-SNE的实现过程：How to Use t-SNE Effectively：https://distill.pub/2016/misread-tsne/

t-SNE算法步骤：

找出高维空间中相邻点之间的成对相似性；
根据高维空间中点的成对相似性，将高维空间中的每个点映射到低维空间；
使用基于Kullback-Leibler散度（KL散度）的梯度下降找到最小化条件概率分布之间的不匹配的低维数据表示；
使用Student-t分布计算低维空间中两点之间的相似度。

③ t-SNE是线性方法还是非线性方法？

t-SNE（t-分布随机邻域嵌入）是一种非线性降维技术，它用于将高维数据集嵌入到低维空间（通常是二维或三维），同时尽可能地保留数据点之间的相对距离。t-SNE的核心思想是将数据点在高维空间的相似度转换为在低维空间中的相似度，并通过优化过程来调整数据点的位置，使得在高维空间中距离较近的点在低维空间中也尽可能地靠近。

t-SNE的非线性特性主要体现在以下几个方面：

概率分布的转换：t-SNE将高维空间中的数据点之间的欧氏距离转换为概率分布，然后通过优化过程将这些概率分布转换为低维空间的相似度。
t分布的使用：t-SNE使用t分布（一种具有重尾的分布）来更好地捕捉数据点之间的距离关系，这与线性降维方法（如PCA）使用的高斯分布不同。
优化过程：t-SNE通过梯度下降或其他优化算法来调整数据点在低维空间中的位置，这个过程是非线性的。
局部结构的保持：t-SNE特别强调保持数据点的局部结构，这通常需要非线性的方式来实现。

因此，t-SNE是一种非线性的降维方法，它在许多情况下能够生成更易于解释和可视化的数据表示。

9、实践

案例：随机生成数据并进行降维

python 复制代码

import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
 
tsne = TSNE(n_components=2)
x = [[1,2,2],[2,2,2],[3,3,3]]
y = [1,0,2]#y是x对应的标签
x_tsne = tsne.fit_transform(x)
plt.scatter(x_tsne[:,0],x_tsne[:,1],c=y)
plt.show()

我自己的代码：在3个同配图和6个异配图上进行t-SNE可视化（在上面代码的基础上改了一丢丢）

Python 复制代码

import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
 
tsne = TSNE(n_components=2)
#x = [[1,2,2],[2,2,2],[3,3,3]]
#y = [1,0,2]#y是x对应的标签
x = features
y = labels
x_tsne = tsne.fit_transform(x)
# 添加标题
plt.title('cora')
plt.scatter(x_tsne[:,0],x_tsne[:,1],c=y)
plt.show()

可视化结果（以cora为例）：

原始空间的t-SNE可视化：

潜在空间的t-SNE可视化：

10、参考资料

Latent space visualization - Deep Learning bits #2：https://hackernoon.com/latent-space-visualization-deep-learning-bits-2-bd09a46920df?source=post_page-----de5a7c687d8d--------------------------------
Use your eyes and Deep Learning to command your computer --- A.I. Odyssey part.2：https://medium.com/hackernoon/talk-to-you-computer-with-you-eyes-and-deep-learning-a-i-odyssey-part-2-7d3405ab8be1
kimi：https://kimi.moonshot.cn/
Autoencoders - Deep Learning bits #1：https://hackernoon.com/autoencoders-deep-learning-bits-1-11731e200694?ref=hackernoon.com
PCA（主要成分分析法）：https://www.cs.cmu.edu/~elaw/papers/pca.pdf?ref=hackernoon.com
ICA：http://www2.hawaii.edu/~kyungim/papers/baek_cvprip02.pdf?ref=hackernoon.com
RGB image：https://www.cs.toronto.edu/~kriz/cifar.html?ref=hackernoon.com
一个卷积自编码器的潜在空间的可视化技术：https://github.com/despoisj/LatentSpaceVisualization?ref=hackernoon.com
实用篇|T-SNE可视化工具详情及代码示例：https://blog.csdn.net/weixin_44649780/article/details/133987875
How to Use t-SNE Effectively：https://distill.pub/2016/misread-tsne/