前言
在数字系统中,加法运算是最常见的算术运算,同时它也是进行各种复杂运算的基础。
半加器
最简单的加法器叫做 半加器 (Half Adder ),它将2个输入1bit的数据相加,输出一个2bits的和,和的范围为0~2(10进制)。和的高位也被称为进位 (Carry ),和的低位则通常被直接叫和 (Sum)。例如:
-
1 + 1 = 2 = 10,即进位carry是1,和sum是0
-
1 + 0 = 1 = 01,即进位carry是0,和sum是1
-
0 + 1 = 1 = 01,即进位carry是0,和sum是1
-
0 + 0 = 0 = 00,即进位carry是0,和sum是0
2个1bit数相加,最多只有4种情况(在上面已经例出来了),据此可以写出半加器的真值表:
| 加数1 | 加数2 | 结果 | 进位 |
|---|---|---|---|
| a | b | sum | carry |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
从这个真值表,不难推断出两个输出的逻辑表达式:
-
和sum在2个输入不同时为1,所以它是输入异或的结果,即 sum = a ^ b
-
进位carry在2个输入都为1时才为1,所以它是输入相与的结果,即 carry = a & b
有了逻辑表达式后,就很容易画出电路图了:
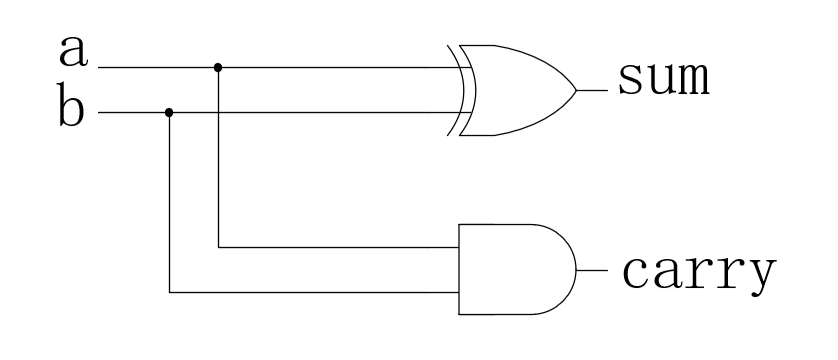
顺便提一句,虽然半加器的基本电路是上面这个样子的,但是在FPGA中,因为只有查找表LUT没有具体的门电路,所以如果用FPGA来综合半加器,它的电路应该是这个样子的(因为只有2个输入和2个输出,所以只要1个LUT6就可以覆盖到所有情况):
如果你不了解LUT,可以看看这篇文章:从底层结构开始学习FPGA(2)----LUT查找表
或者看看这个专栏:从底层结构开始学习FPGA
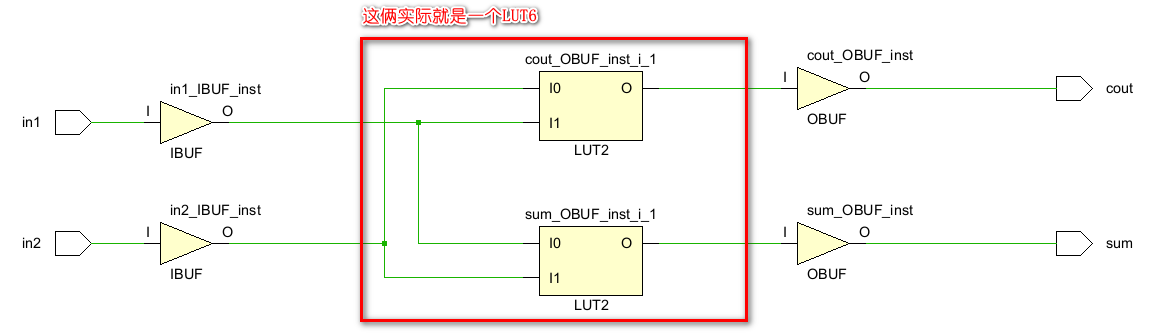
IBUF和OBUF是Vivado自动添加的对输入输出管脚的缓冲,尽管上图显示的是2个LUT2,但是实际上就是1个LUT6,只是这样的显示会更清晰一点。下面的资源显示情况证明了这一点:

用verilog实现半加器的方式有两种:
-
用逻辑表达式来描述输出
-
直接写加法
因为电路非常简单,所以这两种方法综合出来的电路都是一样的(上面说了,就是1个LUT6)。第1种方法:
//使用逻辑表达式来描述半加器
module half_adder(
input in1, //加数1
input in2, //加数2
output sum, //和
output cout //进位
);
//根据化简结果分别表示:和 与 进位
assign sum = in1 ^ in2;
assign cout = in1 & in2;
endmodule 第2种方法:
//直接使用加法(assign语句)进行计算
module half_adder(
input in1, //加数1
input in2, //加数2
output sum, //和
output cout //进位
);
//使用拼接运算符分别表示:和 与 进位
assign {cout,sum} = in1 + in2;
endmodule
//使用always块
module half_adder(
input in1, //加数1
input in2, //加数2
output reg sum, //加和
output reg cout //进位
);
//使用拼接运算符分别表示:和 与 进位
always@(*)begin
{cout,sum} = in1 + in2;
end
endmodule上面分别用always语句和assign语句 来描述半加器加法,但效果上二者是等价的,对于这种比较简单又比较少的语句描述,建议使用assign语句。
有了RTL,接下来就该要写1个对应的TB来测试电路功能是否正常。由于这个电路足够简单(一共只有4种情况),所以我们可以把所有可能的情况都穷举出来,然后观察输出是否符合预期即可。TB如下:
`timescale 1ns/1ns //时间刻度:单位1ns,精度1ns
module tb_half_adder();
//定义变量
reg in1;
reg in2;
wire cout;
wire sum;
//设置初始化条件
initial begin
//第1种情况
in1 =1'b0; //初始化为0
in2 =1'b0; //初始化为0
#10
//第2种情况
in1 =1'b0;
in2 =1'b1;
#10
//第3种情况
in1 =1'b1;
in2 =1'b0;
#10
//第4种情况
in1 =1'b1;
in2 =1'b1;
#10 $stop(); //结束仿真
end
//例化被测试模块
half_adder u_half_adder(
.in1 (in1),
.in2 (in2),
.sum (sum),
.cout (cout)
);
endmodule仿真结果如下:

通过和真值表的对比(或者验证逻辑表达式也可以),可以发现,电路的输出是符合预期的。
全加器
虽然半加器可以实现2个1bit数的加法,但在实际应用中,更常见的是要实现多个bit的加法,那么该如何实现?以2个2bits数的加法为例:
先把低位和高位的加法先分开。
低位是2个1bit的加法,所以可以用1个HA(半加器)来实现,它产生的和就是最终结果的低位,它产生的进位要被送入到高位参与它们的加法。
高位除了要计算2个加数的高位外,还有1个来自低位的进位。
问题是半加器没有设计来自低位的进位,所以它处理不了这种情况。为此,全加器被设计出来了,它在半加器的基础上,增加了来自低级的进位输入。这样多个全加器就可以级联起来实现多bits的加法了。
全加器 (Full Adder ),它将2个1bit的输入和来自低级的进位输入共3个数相加,输出一个2bits的和,和的范围为0~3(10进制)。和的高位也被称为进位 (Carry ),和的低位则通常被直接叫和 (Sum)。例如:
-
1 + 1 + 1 = 3 = 11,即进位carry是1,和sum是1
-
1 + 0 + 1 = 2 = 10,即进位carry是1,和sum是0
-
·····
-
0 + 1 + 0 = 1 = 01,即进位carry是0,和sum是1
-
0 + 0 + 0 = 0 = 00,即进位carry是0,和sum是0
3个输入一共只有8种情况,把所有情况都穷举出来,就可以列出全加器的真值表:
| 加数1 | 加数2 | 低位进位 | 结果 | 高位进位 |
|---|---|---|---|---|
| a | b | cin | sum | cout |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
从这个真值表,不难推断出两个输出的逻辑表达式:
-
和sum为1的4种情况,ab'cin' + a'bcin' +ab'cin + a'bcin = (ab'+ a'b)cin' + (ab'+ a'b)'cin = (a^b)cin' + (a^b)'cin = (a^b)^cin = a ^ b ^ cin
-
进位cout为1的4种情况,abcin' + a'bcin + ab'cin + abcin = ab(cin + cin') + cin(a'b + ab') = ab + cin(a^b)
有了逻辑表达式后,就很容易画出电路图了:
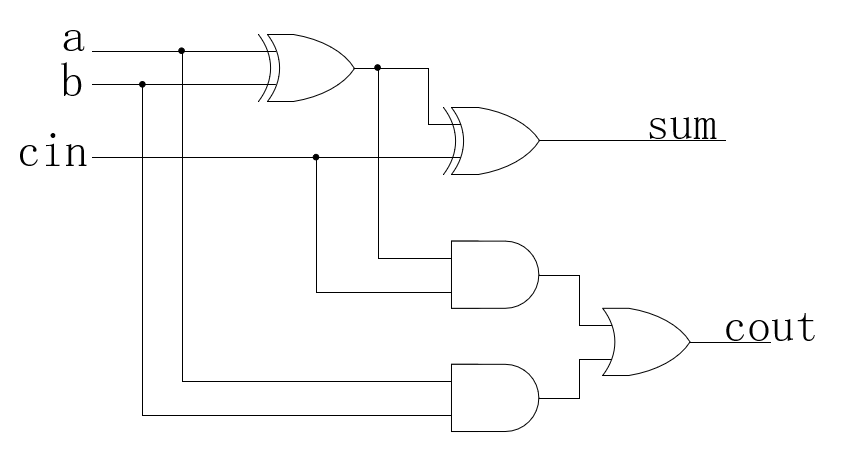
同样的,虽然全加器的基本电路是上面这个样子的,但是在FPGA中,因为只有查找表LUT没有具体的门电路,所以它的电路其实是这个样子的(因为只有3个输入和2个输出,所以只要1个LUT6就可以覆盖到所有情况):
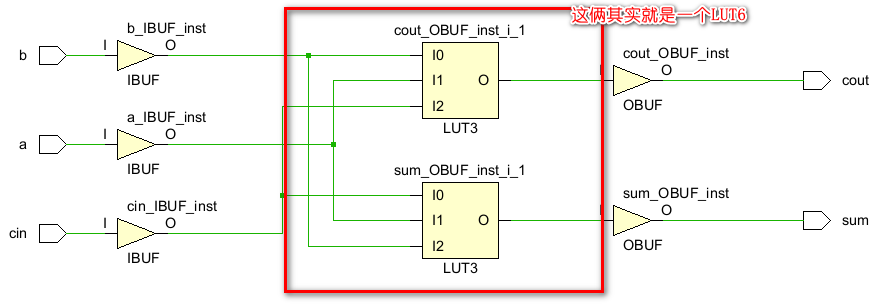
尽管显示的也是2个LUT2,但实际上就是1个LUT6。同半加器一样,全加器的Verilog实现也可以用2种方式:
-
用逻辑表达式来描述输出
-
直接写加法
因为电路非常简单,所以这两种方法综合出来的电路是一样的。第1种方法:
//根据逻辑表达式来描述输出
module full_adder(
input a, //加数1
input b, //加数2
input cin, //低位向高位的进位
output sum, //和
output cout //进位
);
assign sum = a ^ b ^ cin;
assign cout = (a & b) | cin & (a ^ b);
endmodule第2种方法:
//直接用加法来描述全加器
module full_adder(
input a, //加数1
input b, //加数2
input cin, //低位向高位的进位
output sum, //和
output cout //进位
);
assign {cout,sum} = a + b + cin; //使用位拼接 和 加法运算
endmodule
接下来,也写1个TB来测试电路,因为输入一共只有8个,所以依然用穷举法来测试:
`timescale 1ns/1ns //时间刻度:单位1ns,精度1ns
module tb_full_adder();
//定义变量
reg a;
reg b;
reg cin;
wire cout;
wire sum;
//设置初始化条件
initial begin
//第1种情况
a =1'b0;
b =1'b0;
cin =1'b0;
#10
//第2种情况
a =1'b0;
b =1'b1;
cin =1'b0;
#10
//第3种情况
a =1'b1;
b =1'b0;
cin =1'b0;
#10
//第4种情况
a =1'b1;
b =1'b1;
cin =1'b0;
#10
//第5种情况
a =1'b0;
b =1'b0;
cin =1'b1;
#10
//第6种情况
a =1'b0;
b =1'b1;
cin =1'b1;
#10
//第7种情况
a =1'b1;
b =1'b0;
cin =1'b1;
#10
//第8种情况
a =1'b1;
b =1'b1;
cin =1'b1;
#10 $stop(); //结束仿真
end
//例化被测试模块
full_adder u_full_adder(
.a (a),
.b (b),
.sum (sum),
.cin (cin),
.cout (cout)
);
endmodule
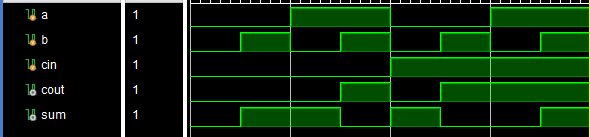
仿真结果如下所示:
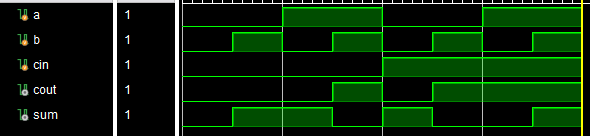
通过和真值表的对比(或者验证逻辑表达式也可以),可以发现,电路的输出是符合预期的。
用半加器实现全加器
如果你仔细看半加器和全加器的电路图,就会发现它们有很多重合的地方:
-
半加器的组成:1个与门 + 1个异或门
-
全加器的组成:2个与门 + 2个异或门 + 1个或门
这么看,全加器似乎可以用2个半加器 + 1个或门组成,我们把全加器的电路图重新布局一下:
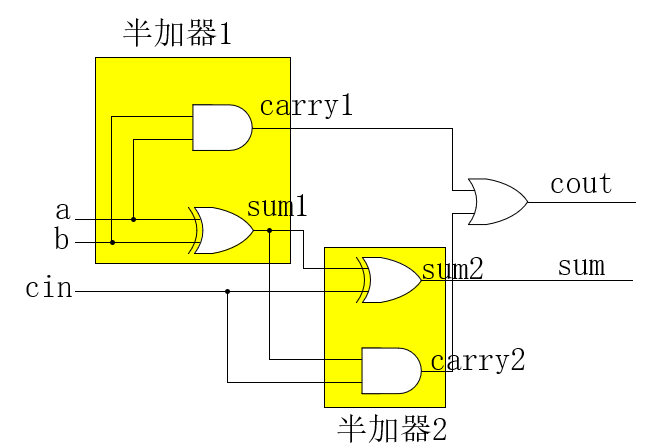
可以清晰地看到,全加器确实可以由2个半加器+1个或门组成:
-
加数a和b作为第1个半加器的输入
-
第1个半加器的输出sum1 和 进位输入cin作为第2个半加器的输入;第1个半加器的输出carry1作为或门的1个输入
-
第2个半加器的输出sum2就是全加器的和sum; 第2个半加器的输出carry2作为或门的另1个输入
-
或门的输出cout就是全加器的进位cout
用Verilog来描述是这样的:
//2个半加器级联实现全加器
module full_adder(
input a, //加数1
input b, //加数2
input cin, //低位向高位的进位
output sum, //和
output cout //进位
);
//模块之间的连线,结合模块图理解
wire hf1_cout; //第1个半加器的进位输出
wire hf2_cout; //第2个半加器的进位输出
wire hf1_sum; //第1个半加器的和输出
assign cout = hf1_cout || hf2_cout;
//例化第1个半加器
half_adder u1_half_adder(
.a (a),
.b (b),
.sum (hf1_sum),
.cout (hf1_cout)
);
//例化第2个半加器
half_adder u2_half_adder(
.a (hf1_sum),
.b (cin),
.sum (sum),
.cout (hf2_cout)
);
endmodule
module half_adder(
input a, //加数1
input b, //加数2
output sum, //和
output cout //进位
);
//使用拼接运算符分别表示:和 与 进位
assign {cout,sum} = a + b;
endmodule
生成的RTL视图如下:
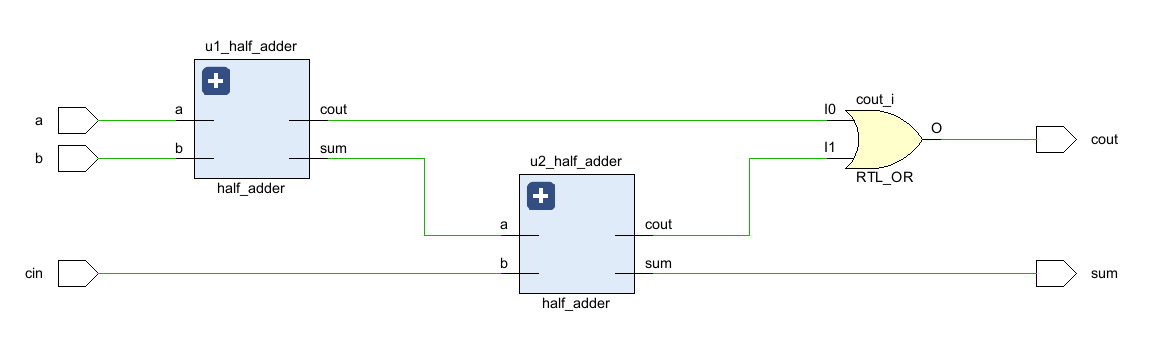
这与理论上的框图一致:例化了2个半加器和1个或门。仿真的话用上面的同一个TB就行,仿真结果也和之前的结果一致: