一个成像系统可以看作一个线性移不变系统,他将理想图像变换为我们所观察到的图像。
相对于与实际相关的线性时不变系统,二维图像线性移不变系统不受因果约束。系统基本特性如下:
1)
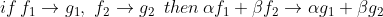
2)
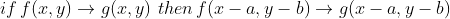
1 点扩散函数
1)冲击函数采样
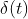
为无限冲击函数,当作用与连续函数时,有
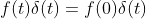
,推导如下:
在
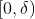
区间,有关系式
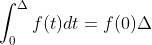
,做如下变换
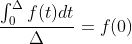
,
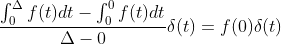
,结论得证。
根据平移性质,有
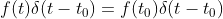
,对两边同时积分得
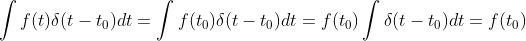
。
当需要对函数 f(t) 在
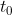
点采样时,可做如下卷积
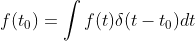
。
2)图像线性分解
对于离散函数,可以写成离散冲击得线性组合
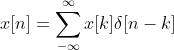
。
对于连续函数,定义
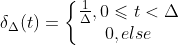
,
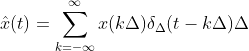
。
当
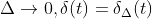
,
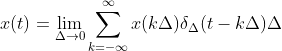
,改写成积分形式为:
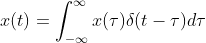
。
二维连续图像函数
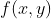
使用二维冲击函数
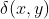
线性组合为
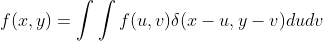
。
对理想二维图像
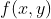
,经过成像系统所得到的结果
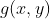
是一个线性变换过程,如果
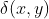
的响应为
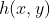
,则
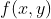
的响应为:
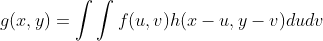
。
以上
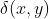
的响应为
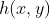
描述了一个理想点经过成像系统后的变化,
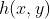
被称为点扩散函数(Point Spread Function)。
由于成像系统为线性变换,上式实际上表示了理想图像与点扩散函数的卷积结果,即
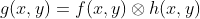
。
2 调制传递函数
点扩散函数在空域中使用卷积来描述成像系统,调制传递函数在频域使用乘积描述成像系统。
函数
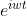
经过成像系统变换为线性变换,使用卷积表示为
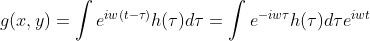
。
上式表明,
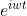
经过成像系统后其频率没有发生改变,仅改变了幅度与相位,
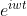
被称为成像系统的特征函数(类似线性代数中的特征向量)。
同样,对于二维图像
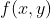
,特征函数
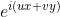
经过线性变换结果为:
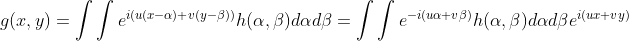
。
在
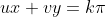
平行线组垂直方向上,波长为
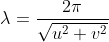
的余弦波的调制传递函数(Modulation Transfer Function) 为:
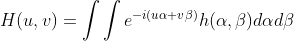
,使用变换
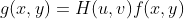
描述二维频率为
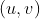
的响应幅度与相位。