文章目录
证明收敛?
-
对于Value迭代:不动点证明的思路
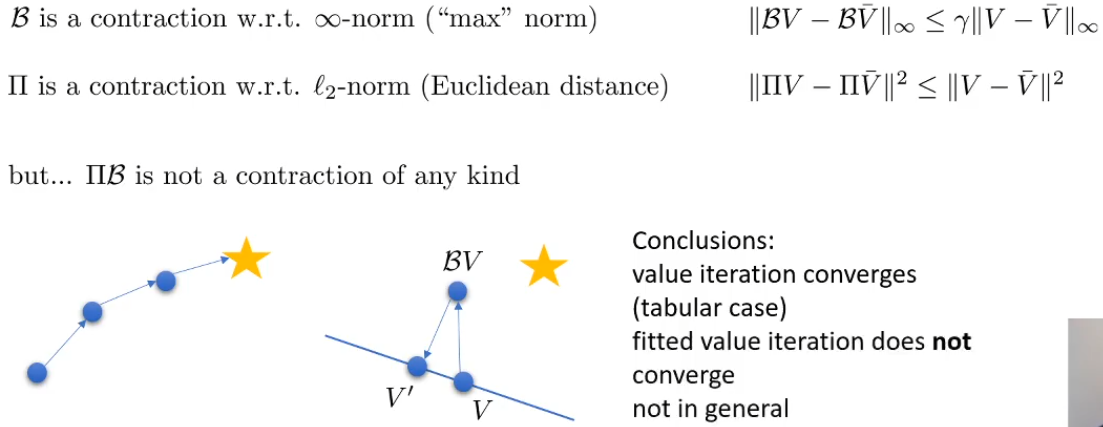
首先定义一个算子 B : B V = max a r a + γ T a V \mathcal{B}:\mathcal{B}V=\max_ar_a+\gamma\mathcal{T}_aV B:BV=maxara+γTaV
接着有一个不动点 V ∗ ( s ) = max a r ( s , a ) + γ E [ V ∗ ( s ′ ) ] V^*(s)=\max_{a}r(s,a)+\gamma E[V^*(s')] V∗(s)=maxar(s,a)+γE[V∗(s′)],有 V ∗ = B V ∗ V^*=\mathcal{B}V^* V∗=BV∗
每次使用算子都会,V离不动点的距离有收缩: ∣ ∣ B V − V ∗ ∣ ∣ ∞ ≤ γ ∣ ∣ V − V ∗ ∣ ∣ ∞ ||\mathcal{B}V-V^*||\infty\leq\gamma||V-V^*||{\infty} ∣∣BV−V∗∣∣∞≤γ∣∣V−V∗∣∣∞
-
对于神经网络拟合的Value迭代:对于监督学习,也是得到一个 V ′ V' V′使得距离 ∣ ∣ V ′ ( s ) − ( B V ) ( s ) ∣ ∣ 2 ||V'(s)-(\mathcal{B}V)(s)||^2 ∣∣V′(s)−(BV)(s)∣∣2最小------投影
V的迭代是这样的 V ← Π B V V\leftarrow \Pi\mathcal{B}V V←ΠBV
定义一个新的算子 Π : Π V = arg max V ′ ∈ Ω 1 2 ∑ ∣ ∣ V ′ ( s ) − V ( s ) ∣ ∣ 2 \Pi:\Pi V=\arg\max_{V'\in\Omega}\frac{1}{2}\sum||V'(s)-V(s)||^2 Π:ΠV=argmaxV′∈Ω21∑∣∣V′(s)−V(s)∣∣2, Π \Pi Π实际上是用l2范数对 Ω \Omega Ω的投影,也是收缩的
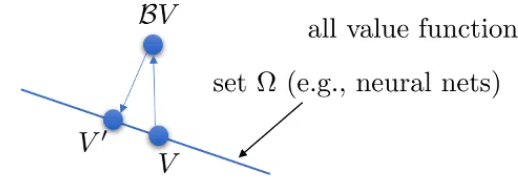
!收缩:
∣ ∣ Π V − Π V ˉ ∣ ∣ 2 ≤ ∣ ∣ V − V ˉ ∣ ∣ 2 ||\Pi V-\Pi \bar{V}||^2\leq||V-\bar{V}||^2 ∣∣ΠV−ΠVˉ∣∣2≤∣∣V−Vˉ∣∣2**(注意这里用的是2范数而上面是无穷范数,两种算子都是再各自的范数上收缩的),但是把两个算子结合在一起就不会收缩了**
所以就导致了使用Q-table能够保证收敛,而用神经网络拟合的V的Q-iteration不能够收敛
- 对于Q-iteration
和上面一样,用神经网络拟合时不收敛,因为有投影算子 - 对于A-C
也是再用神经网络拟合的时候不收敛
尽管理论上令人沮丧,但是实际中可以表现的很好!
Deep RL with Q-Functions

这里面包含了replay buffer和target network,但是暂时不细说了。
Polyak averaging:模型平均的问题
Double Q-Learning
在实际的使用过程中,Q-Learning总是出现overestimate的问题:估计的价值比实际的价值高很多:
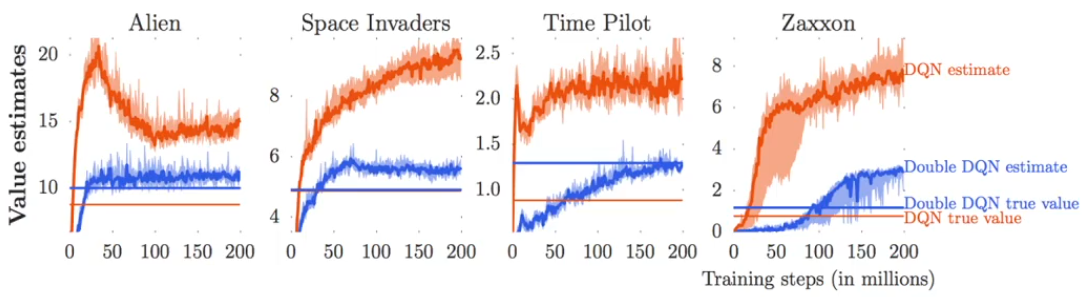
为什么会出现这样呢:
我们的target value是 y i = r i + γ max a j ′ Q ϕ ′ ( s j ′ , a j ′ ) y_i=r_i+\gamma\max_{a'j}Q{\phi'}(s'_j,a'_j) yi=ri+γmaxaj′Qϕ′(sj′,aj′),其中 ϕ ′ \phi' ϕ′是当前的价值函数
imagine we have two random variables: X 1 , X 2 X_1,X_2 X1,X2,We have E [ max ( X 1 , X 2 ) ] ≥ max ( E [ X 1 ] , E X 2 ) E[\max(X_1,X_2)]\ge\max(E[X_1],E{X_2}) E[max(X1,X2)]≥max(E[X1],EX2)
而对于 Q ϕ ′ ( s ′ , a ′ ) Q_{\phi'}(s',a') Qϕ′(s′,a′),它是对真正Q函数的估计,也就是真正的Q函数加上一些"噪声",所以当我们取 Q ϕ ′ ( s ′ , a ′ ) Q_{\phi'}(s',a') Qϕ′(s′,a′)的最大值的时候,尽管"噪声"是无偏的,也会导致最后的值变大:
max a ′ Q ϕ ′ ( s ′ , a ′ ) = Q ϕ ′ ( s ′ , arg max a ′ Q ϕ ′ ( s ′ , a ′ ) ) \max_{a'}Q_{\phi'}(s',a')=Q_{\phi'}(s',\arg\max_{a'} Q_{\phi'}(s',a')) a′maxQϕ′(s′,a′)=Qϕ′(s′,arga′maxQϕ′(s′,a′))
为什么有上面这个式子的写法? 别忘了遵循贪婪(没有"探索")的策略,我们选择下一个action就是根据 Q ϕ ′ Q_{\phi'} Qϕ′的,因为是根据 arg max \arg\max argmax选出来的,因此如果我们选择了正的噪声的action作为价值函数的输入,那么价值函数会基于同样的贪婪也会选择正的噪声,就会overestimate。

理论上的解法
因此,提出了Double Q-Learning,我们分别使用两个神经网络去产生动作和估计价值,这样两个神经网络拟合时产生的"噪声"就是不相关的!------这个操作非常像通信里面的啊!
Q ϕ A ( s , a ) = r + γ Q ϕ B ( s ′ , arg max a ′ Q ϕ A ( s ′ , a ′ ) ) Q_{\phi_A}(s,a)=r+\gamma Q_{\phi_B}(s',\arg\max_{a'} Q_{\phi_A}(s',a')) QϕA(s,a)=r+γQϕB(s′,arga′maxQϕA(s′,a′))
Q ϕ B ( s , a ) = r + γ Q ϕ B ( s ′ , arg max a ′ Q ϕ B ( s ′ , a ′ ) ) Q_{\phi_B}(s,a)=r+\gamma Q_{\phi_B}(s',\arg\max_{a'} Q_{\phi_B}(s',a')) QϕB(s,a)=r+γQϕB(s′,arga′maxQϕB(s′,a′))
实际上的解法
实际上,我们不需要麻烦的创造一个动作选择神经网络,一个价值神经网络,而是直接利用现成的:

别忘了我们其实有两个 ϕ \phi ϕ和 ϕ ′ \phi' ϕ′的,一个表示目标函数,另一个则是不断更新的,而目标函数会定期更新,因此我们直接借助这两个现成的:
y i = r i + γ Q ϕ ′ ( s j ′ , arg max a ′ Q ϕ ( s ′ , a ′ ) ) y_i=r_i+\gamma Q_{\phi'}(s'j,\arg\max{a'}Q_{\phi}(s',a')) yi=ri+γQϕ′(sj′,arga′maxQϕ(s′,a′))
上面利用当前的神经网络去确定动作action,而利用目标网络去确定价值value
DDPG: Q-Learning with continuous actions
- 各种对连续动作采样的方法
- DDPG
回忆一下,我们的目标是 max a Q ϕ ( s , a ) = Q ϕ ( s , arg max a Q ϕ ( s , a ) ) \max_a Q_{\phi}(s,a)=Q_{\phi}(s,\arg\max_{a}Q_{\phi}(s,a)) maxaQϕ(s,a)=Qϕ(s,argmaxaQϕ(s,a))
因此,想办法训练另一个网络 μ θ ≈ arg max a Q ϕ ( s , a ) \mu_\theta\approx\arg\max_a Q_\phi(s,a) μθ≈argmaxaQϕ(s,a),它可以看作是一个状态-动作函数,用来模拟 arg max \arg\max argmax的过程
怎么去寻找这个网络的参数呢?因为我们是寻找最大的Q,因此用梯度上升就可以 d Q ϕ d θ = d a d θ d Q ϕ d a \frac{dQ_\phi}{d\theta}=\frac{da}{d\theta}\frac{dQ_\phi}{da} dθdQϕ=dθdadadQϕ
新的target: y j = r j + γ Q ϕ ′ ( s j ′ , μ θ ( s j ′ ) ) ≈ r j + γ Q ϕ ′ ( s j ′ , arg max a ′ Q ϕ ′ ( s j ′ , a j ′ ) ) y_j=r_j+\gamma Q_{\phi'}(s'j,\mu\theta(s'j))\approx r_j+\gamma Q{\phi'}(s'j,\arg\max{a'}Q_{\phi'}(s'_j,a'_j)) yj=rj+γQϕ′(sj′,μθ(sj′))≈rj+γQϕ′(sj′,argmaxa′Qϕ′(sj′,aj′))

Advanced tips for Q-Learning
- Q-Learning再不同问题上的稳定度很不同,因此需要首先确保稳定性,包括选择合适的随机数种子。
- 较大的replay buffer能够帮助提高稳定性
- Looks more like fitted Q-iteration
- 学习可能需要很长时间才能有突破
- 进行探索的时候,先把 ϵ \epsilon ϵ设置大一点,随后慢慢的逐步减小
- Bellman error gradients can be big: clip gradients or use Huber loss instead L = { x 2 / 2 if ∣ x ∣ ≤ δ δ ∣ x ∣ − δ 2 / 2 otherwise L=\begin{cases} x^2/2& \text{ if } |x|\leq\delta \\ \delta|x|-\delta^2/2& \text{ otherwise } \end{cases} L={x2/2δ∣x∣−δ2/2 if ∣x∣≤δ otherwise
- 多使用Double Q-Learning,非常好用
- 变化的学习率或者Adam optimizer会很有帮助