1、tips
1.1、set求交集
{1,2,3} & {2,3} & {1,2} = {2} 其实就是位运算, 只有set可以这样使用, list没有这种用法
{1,2,3} | {2,3, 4} | {1,2} = {1, 2, 3, 4} 并集
1.2、*与**
*
- 序列(列表、元组)解包,如果是字典,那解包之后得到key
- 在函数传递中使用*arg
python
list1 = [[1,2,3],[4,5,6],[7,8,9]]
print(*list1) # [1, 2, 3] [4, 5, 6] [7, 8, 9]
list2 = [1,2,3]
print(*list2) # 1 2 3
my_dict = {'arg':77,'list':88,'name':'B'}
print(*my_dict) # arg list name**
- 字典拼接
- 在函数传递中使用**kwargs
python
my_dict1 = {'arg':77,'list':88,'name':'B'}
my_dict2 = {'value':99}
my_dict_new = {**my_dict1, **my_dict2}
print(my_dict_new) # {'arg': 77, 'list': 88, 'name': 'B', 'value': 99}1.3、矩阵(zip)
zip函数是Python中的一个内置函数,在Python 2.X的版本中返回的是一个列表,Python 3.X版本中返回的是一个zip迭代器对象。
利用zip这一特性,可实现矩阵旋转
1.3.1、旋转矩阵
python
list1 = list(zip([1,2,3],[4,5,6]))
print(list1) # [(1, 4), (2, 5), (3, 6)]
list2 = list(zip([1,2,3],[4,5,6,7])) # 长度不等时,以最短长度为准
print(list2) # [(1, 4), (2, 5), (3, 6)]
list3 = list(zip([1,2,3,4],'def'))
print(list3) # [(1, 'd'), (2, 'e'), (3, 'f')]
# n*n矩阵逆时针旋转90度
matrix = [[1,2,3],[4,5,6],[7,8,9]]
res = list(zip(*matrix))[::-1]
print(res) # [(3, 6, 9), (2, 5, 8), (1, 4, 7)]
# n*n矩阵顺时针旋转90度
matrix = [[1,2,3],[4,5,6],[7,8,9]]
res = [row[::-1] for row in zip(*matrix)]
print(res) # [(7, 4, 1), (8, 5, 2), (9, 6, 3)]1.3.2、螺旋矩阵
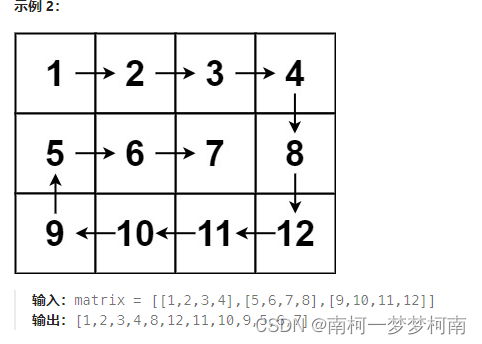
示例中的矩阵先选取第一行,剩余矩阵逆时针旋转90度得到
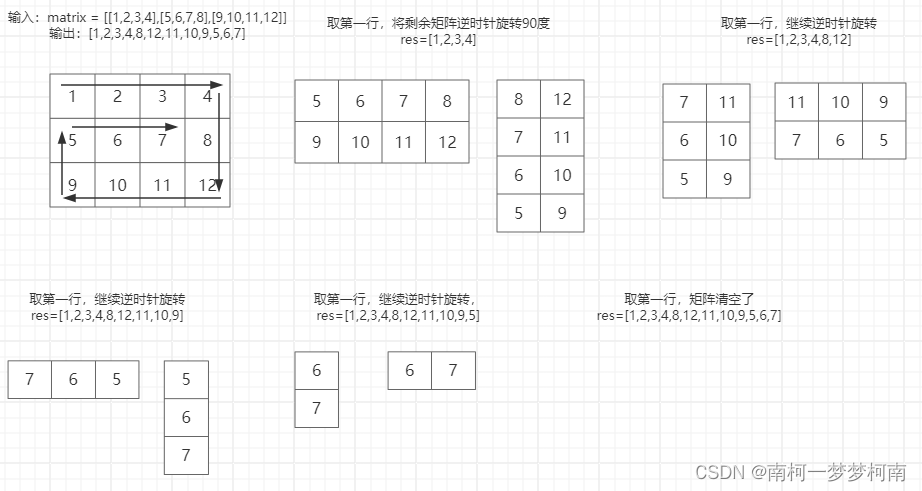
python
class Solution(object):
def spiralOrder(self, matrix):
res = []
while matrix:
res.extend(matrix.pop(0))
matrix = list(zip(*matrix))[::-1]
return res
print(Solution().maxSubArray([[1,2,3],[4,5,6],[7,8,9]]))
print(Solution().maxSubArray([[1,2,3,4],[5,6,7,8],[9,10,11,12]]))
[1, 2, 3, 6, 9, 8, 7, 4, 5]
[1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7]
python
class Solution(object):
def generateMatrix(self, n):
'''
在54题螺旋矩阵中,按顺时针顺序返回所有元素
取矩阵第一行,然后逆时针旋转矩阵,直至矩阵为空
这一题是54题的逆转,也就是从终点开始先顺时针旋转,然后插入首行元素
matrix = [[1,2,3],[8,9,4],[7,6,5]]
res = []
while matrix:
res.append(matrix.pop(0))
matrix = list(zip(*matrix))[::-1]
'''
nums = [i+1 for i in range(n*n)]
matrix = [[nums[-1]]]
nums.pop()
while nums:
matrix = [list(row[::-1]) for row in zip(*matrix)] # 顺时针旋转
len_matrix = len(matrix[0])
matrix.insert(0, nums[-len_matrix:]) # 取nums后面len_matrix个元素,插入矩阵第一行
del nums[-len_matrix:] # 移除nums后面len_matrix个元素
return matrix
print(Solution().generateMatrix(4))
[[1, 2, 3, 4], [12, 13, 14, 5], [11, 16, 15, 6], [10, 9, 8, 7]]
'''
[1, 2, 3, 4]
[12, 13, 14, 5]
[11, 16, 15, 6]
[10, 9, 8, 7]
'''
python
# 或者由四个边界遍历
class Solution(object):
def generateMatrix(self, n):
result = [[0]*n for i in range(n)]
count = 0
left, right, up, down = 0, n-1, 0, n-1
while count < n*n:
for i in range(left, right+1): # 上边界
count += 1
result[up][i] = count
up += 1
for i in range(up, down+1): # 右边界
count += 1
result[i][right] = count
right -= 1
for i in range(right,left-1,-1): # 下边界
count += 1
result[down][i] = count
down -= 1
for i in range(down,up-1,-1): # 左边界
count += 1
result[i][left] = count
left += 1
return result
print(Solution().generateMatrix(4))
[[1, 2, 3, 4], [12, 13, 14, 5], [11, 16, 15, 6], [10, 9, 8, 7]]1.4、ASCII转换
python
# 字符转ASCII ord
asc = ord('a')
print(asc) # 97
# ASCII转字符 chr
ch = chr(100)
print(97)利用这一特性,一些有规律的字符就可以用数字来表示
比如 a-z 26个字母用一个二十六位的二进制来表示
python
print(ord('z')-ord('a')) # 25
# a 就是左移0位 z就是左移25位
print('a', 1<<0, format(1<<0, '0b'))
print('b', 1<<1, format(1<<1, '0b'))
print('c', 1<<2, format(1<<2, '0b'))
print('d', 1<<3, format(1<<3, '0b'))
# 那么字符串'acg'或'gca'可以表示为
s = 'acg'
res = 0
for i in s:
res = res | 1<<(ord(i)-ord('a'))
print(res, format(res, '0b')) # 69 1000101
s = 'gca'
res = 0
for i in s:
res = res | 1<<(ord(i)-ord('a'))
print(res, format(res, '0b')) # 69 10001011.5、sort与sorted
python
# sort()是list的方法 没有返回值, str就没有这种方法
list1 = [3,2,5]
list1.sort()
print(list1) # [2, 3, 5]
# sorted是python内置方法,可以对序列排序,因此可以对str、tuple、list排序,返回值为list
print(sorted('daf')) # ['a', 'd', 'f']
print(sorted(['d', 'a', 'f'])) # ['a', 'd', 'f']
print(sorted(('d', 'a', 'f'))) # ['a', 'd', 'f']1.6、字典序
字典序,又称字母序,用于比较任意序列对应ASCII数值的大小,从序列左边第一个字符开始比较,大者为大,小者为小,若相等再比较下一个字符。
示例:下一个排列

python
"""
找下一个字典序更大的序列
1、倒序遍历数组中的元素,找到第一个相邻的升序序列(i,j),那么i后面的序列是降序
2、找到i右侧序列中第一个大于nums[i]的元素,将两者交互位置,交换位置之后i后面的序列还是降序的
3、再将i后面的序列变成升序,即反转,就得到了下一个字典序更大的序列
如:
[1,3,5,4,3,2] 从后往前找升序序列[3,5], i=1
i=1后面从后往前找比nums[1]=3大的数 nums[3]=4,交换位置得到[1,4,5,3,3,2]
将i=2后的降序序列反转[1,4,2,3,3,5]
"""
class Solution(object):
def nextPermutation(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
length = len(nums)
if length <= 1:
return nums
left = length-2
while left >= 0 and nums[left] >= nums[left+1]:
left -= 1
if left == -1:
nums.reverse()
return nums
right = length-1
while left < right:
if nums[left] < nums[right]:
nums[left], nums[right] = nums[right], nums[left]
break
else:
right -= 1
l, r = left+1, length-1
while l < r:
nums[l], nums[r] = nums[r], nums[l]
l += 1
r -= 1
return nums1.7、位运算
原码:最高位是符号位,0代表正数,1代表负数,非符号位为二进制数字
反码:正数的反码与原码一致,负数的反码符号位不变,其余取反
补码,正数的补码与原码一致,负数的补码为其反码加1
补码转换为原码:正数与补码一致,负数符号位不变,其余按位取反+1
反码变原码:正数与原码一致,负数符号位不变,其余按位取反
如-5:原码:1101 反码1010 补码1011
|----|----|----|----|------|--------|
| 与 | 或 | 非 | 异或 | 右移 | 无符号右移 |
| & | | | ~ | ^ | >> | >>> |
异或的性质:
- 交换律:A ^ B = B ^ A;
- 结合律:A ^ (B ^ C) = (A ^ B) ^ C;
- 恒等律:X ^ 0 = X;
- 归零律:X ^ X = 0;
- 自反:A ^ B ^ B = A ^ 0 = A;
- 对于任意的 X: X ^ (-1) = ~X;
- 如果 A ^ B = C 成立,那么 A ^ B = C,B ^ C = A;
应用:
- 异或:
- ①1-1000放在含有1001个元素的数组中,只有唯一的一个元素重复,找出这个重复的数字,如果令1 ^ 2 ^ ... ^ 1000(序列中不包含n)的结果为T,那么1 ^ 2 ^ ... ^ 1000(序列中包含n)的结果就是 T^n,T ^ (T ^ n) = n;
- ②假设有一个变量15,二进制表示为0000 1111,将第3,4,8位取反,0000 1111 ^ 1000 1100 = 1000 0011;
- ③a = 15(0000 1111), b= 23(0001 0111),将两个变量交换,a = a ^ b;b = b ^ a;a = a ^ b ;原理:a和b异或,可以把结果x看作是a、b互为密码子进行加密;将x,同b(原值)异或,也就是把b作为密码子,因此可以还原a,赋值给b;将x,同b(此时为a)异或,也就是把b(此时为a)作为密码子,因此还原出的值为原b,赋值给a。交换结束。
- ④两值相等,a ^ b == 0
- 与:
- ①清零,a&0=0;
- ②X=10101110,取X的低4位,用 X & 0000 1111 = 00001110 即可得到
- 或:将X=10100000的低4位置1 ,用X | 0000 1111 = 1010 1111即可得到
- 非:使一个数的最低位为零,可以表示为:a&~1,~1的值为1111111111111110,再按"与"运算,最低位一定为0
- 移位:
- 左移<<:a = a<< 2将a的二进制位左移2位,右补0
- 右移>>:将一个数的各二进制位全部右移若干位,正数左补0,负数左补1,右边丢弃,(负数以原码的补码表示,即最高位补1,-5就是10000000 00000000 00000000 00000101),-31>>2=-8
- 去掉最后一位:a>>1
- 在最后一位加一个0:a<<1
- 在最后一位加一个1:a<<1+1
- 将最后一位变为1:a|1
- 将最后一位变为0:a|1-1
- 将最后一位取反:a^1
- 把右数的第k位变为1:a|(1<<(k-1))
- 把右数的k位变为0:a&(~(a<<(k-1)))
- 把右数的k位取反:a^(1<<(k-1))
- 取末k位:a&((1<<k)-1)
- 取右数的第k位:x>>(k-1)&1
- 把末k位全变为1:x|((1<<k)-1)
- 把末k位取反:x^((1<<k)-1)
- 把右边连续的1变为0:x&(x+1)
- 把右边第一个0变为1:x|(x+1)
- 把右边连续的0变为1:x|(x-1)
- 取右边连续的1:(x^(x+1))>>1
- 去掉右起的第一个1的左边:x&(x^(x-1))
- a除以b=2**k取余:a&(b-1)
python
'''
给你一个非空整数数组 nums
除了某个元素只出现一次以外,其余每个元素均出现两次。
找出那个只出现了一次的元素。
'''
class Solution(object):
def singleNumber(self, nums):
ans = 0
for num in nums:
ans = ans ^ num
return ans
print(Solution().singleNumber([4,1,2,1,2])) # 4
'''
给你一个整数数组nums,
除某个元素仅出现一次外,其余每个元素都恰出现三次
请你找出并返回那个只出现了一次的元素
'''
class Solution(object):
def singleNumber(self, nums):
sum1,sum2 = sum(nums),sum(set(nums))
return sum2-(sum1-sum2)//2
print(Solution().singleNumber(nums = [2,2,3,2])) # 3
'''
位运算
第i个格雷码公式为: num = i ^ (i//2)
'''
# class Solution:
# def grayCode(self, n):
# ans = [0] * (1 << n)
# for i in range(1 << n):
# ans[i] = (i >> 1) ^ i
# return ans
'''
n=1 [0,1]
n=2 [0,1,3,2]
n=3 [0,1,3,2,6,7,5,4]
n=4 [0,1,3,2,6,7,5,4,12,13,15,14,10,11,9,8]
[3,2]是[1,0]+2
[6,7,5,4] 是 [2,3,1,0] + 4
可以总结一个规律,n位格雷编码的后2**(n-1)位是n-1位格雷编码的倒序+ 2**(n-1)
'''
class Solution(object):
def grayCode(self, n):
###公式法
res,temp=[0],1
for i in range(n):
for j in range(len(res)-1,-1,-1):
res.append(res[j]+temp)
temp<<=1
return res
print(Solution().grayCode(4))
# [0, 1, 3, 2, 6, 7, 5, 4, 12, 13, 15, 14, 10, 11, 9, 8]2、排序
10种经典排序算法包括冒泡排序、插入排序、选择排序、快速排序、归并排序、堆排序、希尔排序、计数排序、桶排序、基数排序等。
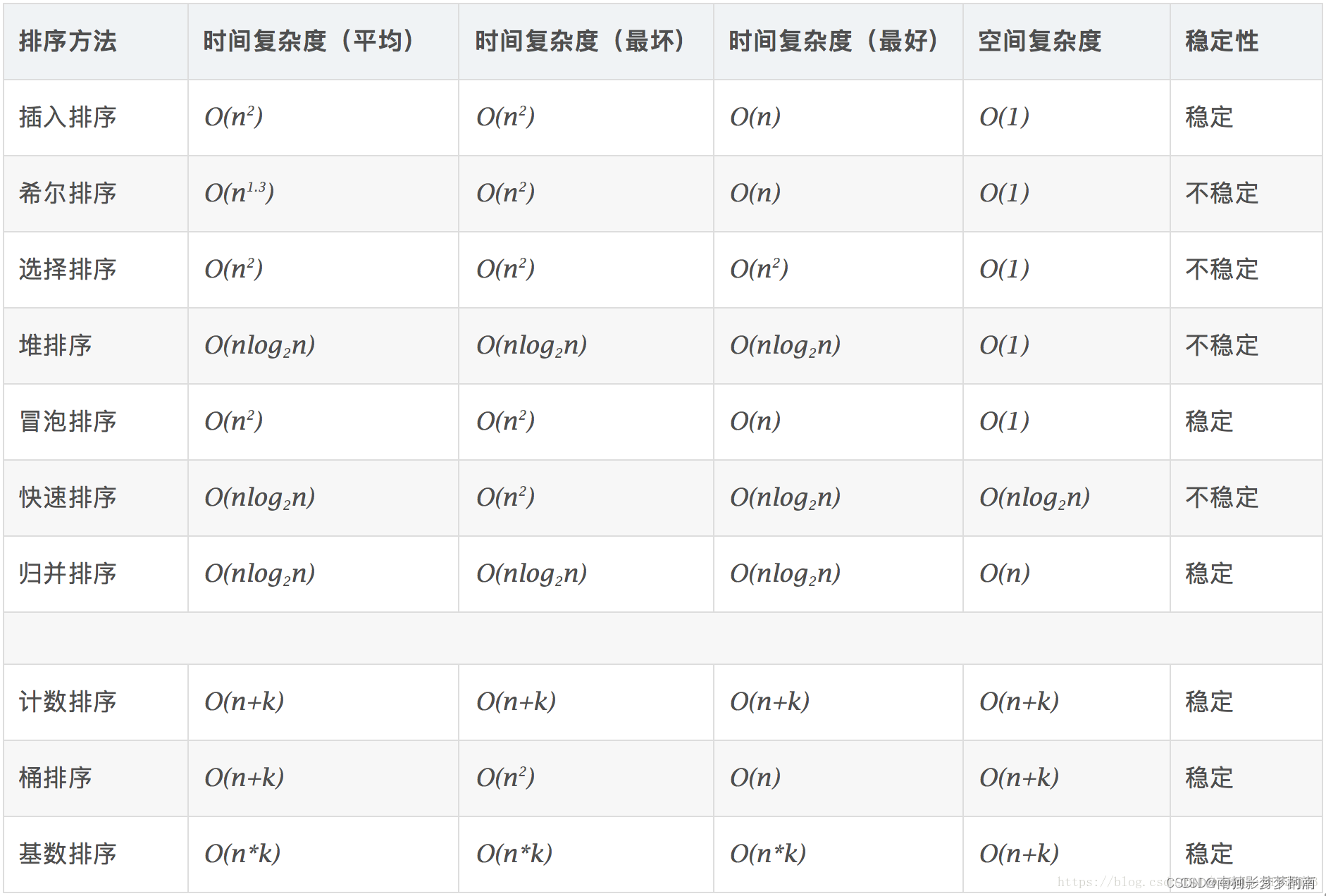
2.1、冒泡排序:Bubble Sort
时间复杂度:O(n^2),空间复杂度:O(1)
原理(从小到大):
- 比较相邻的元素。如果第一个数比第二个数大,就交换它们两个;
- 对每一对相邻元素作同样操作,从开始第一对到结尾的最后一对,得到一个最大值;
- 对除去最大值的剩余序列重复上面的操作,最后得到从小到大的序列;
python
# 冒泡排序,从小到大
def bubbleSort(data):
n = len(data)
print(data,n)
for i in range(0, n):
for j in range(n-i-1):
if data[j] > data[j+1]:
data[j], data[j+1] = data[j+1], data[j]
print(data)
return data
data = [23, 68, 1, 6, 10, 8, 99, 66]
bubbleSort(data)
'''
[23, 68, 1, 6, 10, 8, 99, 66] 8
[23, 1, 6, 10, 8, 68, 66, 99]
[1, 6, 10, 8, 23, 66, 68, 99]
[1, 6, 8, 10, 23, 66, 68, 99]
[1, 6, 8, 10, 23, 66, 68, 99]
[1, 6, 8, 10, 23, 66, 68, 99]
[1, 6, 8, 10, 23, 66, 68, 99]
[1, 6, 8, 10, 23, 66, 68, 99]
[1, 6, 8, 10, 23, 66, 68, 99]
'''
python
# 冒泡排序,从小到大
def bubbleSort(data):
n = len(data)
print(data,n)
for i in range(n):
for j in range(i,0,-1):
if data[j] < data[j-1]:
data[j], data[j-1] = data[j-1], data[j]
print(data)
return data
data = [23, 68, 1, 6, 10, 8, 99, 66]
bubbleSort(data)
'''
[23, 68, 1, 6, 10, 8, 99, 66] 8
[23, 68, 1, 6, 10, 8, 99, 66]
[23, 68, 1, 6, 10, 8, 99, 66]
[1, 23, 68, 6, 10, 8, 99, 66]
[1, 6, 23, 68, 10, 8, 99, 66]
[1, 6, 10, 23, 68, 8, 99, 66]
[1, 6, 8, 10, 23, 68, 99, 66]
[1, 6, 8, 10, 23, 68, 99, 66]
[1, 6, 8, 10, 23, 66, 68, 99]
'''2.2、插入排序:Insort Sort
时间复杂度:O(n^2) ,空间复杂度:O(1)
插入排序和冒泡原理差不多
原理:
- 将第一个元素当作已经排序好的序列
- 拿第二个元素和第一个元素作对比,得到排好序的序列
- 拿第三个元素和已经排序好的序列前往后作比较,找到合适位置插入
- 重复上述操作
python
def insertSort(data):
for i in range(1, len(data)):
for j in range(i, 0, -1):
if data[j] < data[j - 1]:
data[j], data[j - 1] = data[j - 1], data[j]
else:
break
print(data)
return data
arr = [23, 68, 1, 6, 10, 8, 99, 66]
arr = insertSort(arr)
print(f'结果:{arr}')
'''
[23, 68, 1, 6, 10, 8, 99, 66]
[1, 23, 68, 6, 10, 8, 99, 66]
[1, 6, 23, 68, 10, 8, 99, 66]
[1, 6, 10, 23, 68, 8, 99, 66]
[1, 6, 8, 10, 23, 68, 99, 66]
[1, 6, 8, 10, 23, 68, 99, 66]
[1, 6, 8, 10, 23, 66, 68, 99]
结果:[1, 6, 8, 10, 23, 66, 68, 99]
'''
python
def insertSort(data):
for i in range(1, len(data)):
j = 0
while j < i:
if data[j] < data[i]:
j += 1
else:
break
print(data[i],'\t',data[j],'\t',data)
data.insert(j, data.pop(i)) # 将i位置的数字插入到j坐标
return data
arr = [23, 68, 1, 6, 10, 8, 99, 66]
arr = insertSort(arr)
print(f'结果:{arr}')
'''
68 68 [23, 68, 1, 6, 10, 8, 99, 66]
1 23 [23, 68, 1, 6, 10, 8, 99, 66]
6 23 [1, 23, 68, 6, 10, 8, 99, 66]
10 23 [1, 6, 23, 68, 10, 8, 99, 66]
8 10 [1, 6, 10, 23, 68, 8, 99, 66]
99 99 [1, 6, 8, 10, 23, 68, 99, 66]
66 68 [1, 6, 8, 10, 23, 68, 99, 66]
结果:[1, 6, 8, 10, 23, 66, 68, 99]
'''2.3、选择排序:Select Sort
时间复杂度:O(n^2) ,空间复杂度:O(1)
原理:
- 将第一个元素当作已经排序好的序列
- 从剩余元素中分别和第一个元素做对比,找到最小值
- 交换两者位置
- 重复以上操作
python
def selectionSort(num):
n = len(num)
for i in range(n-1):
minIndex = i # i左边是已排序的数组,右边是未排序的数组
for j in range(i+1, n):
if num[j] < num[minIndex]:
minIndex = j
print(num, num[i], num[minIndex])
num[minIndex], num[i] = num[i], num[minIndex]
return num
arr = selectionSort([23, 68, 1, 6, 10, 8, 99, 66])
print(f'结果: {arr}')
'''
[23, 68, 1, 6, 10, 8, 99, 66] 23 1
[1, 68, 23, 6, 10, 8, 99, 66] 68 6
[1, 6, 23, 68, 10, 8, 99, 66] 23 8
[1, 6, 8, 68, 10, 23, 99, 66] 68 10
[1, 6, 8, 10, 68, 23, 99, 66] 68 23
[1, 6, 8, 10, 23, 68, 99, 66] 68 66
[1, 6, 8, 10, 23, 66, 99, 68] 99 68
结果: [1, 6, 8, 10, 23, 66, 68, 99]
'''2.3、快速排序:Quick Sort
时间复杂度:O(logn)~O(n^2)
快速排序使用的是分治法思想
在最理想的状态下,快速排序刚好平衡划分,这种情况下快速排序的运行速度将大大上升。好在快速排序平均情况下的运行时间与其最佳情况下的运行时间相近,也是O(nlogn),因此快速排序是所有内部排序算法中平均性能最优的算法。另外,快速排序是不稳定的。
原理:
- 找到一个基准数,取序列中最中间的一个数
- 小于这个数字的放在左边序列,大于这个数的放在右边序列
- 在对左边和右边的序列重复上述操作知道排序完成
如对 [23, 68, 1, 6, 10, 8, 99, 66] 排序
第一次:[1, 6, 8] [10] [23, 68, 99, 66]
第二次:[1] [6] [8] [10] [23, 68, 99, 66]
第三次:[1] [6] [8] [10] [23, 68, 66] [99]
第四次:[1] [6] [8] [10] [23, 66] [68] [99]
第五次:[1] [6] [8] [10] [23] [66] [68] [99]
python
def quickSort(data):
if len(data) > 1:
mid_index = len(data) // 2
mid = data[mid_index]
data.pop(mid_index)
left, right = [], []
print(data, mid)
for num in data:
if num >= mid:
right.append(num)
else:
left.append(num)
return quickSort(left) + [mid] + quickSort(right)
else:
return data
arr = [23, 68, 1, 6, 10, 8, 99, 66]
arr = quickSort(arr)
print(arr)
'''
[23, 68, 1, 6, 8, 99, 66] 10
[1, 8] 6
[23, 68, 66] 99
[23, 66] 68
[23] 66
[1, 6, 8, 10, 23, 66, 68, 99]
'''2.4、归并排序:Merge Sort
时间复杂度:O(nlogn),空间复杂度:O(n)
归并排序使用的也是分治法思想
原理:
- 将数组递进地对半分组,直到每组仅剩一个元素
- 两两之间归并,将两个较短的已排序的数组合并为一个较长的排序的数组
python
def mergeSort(data):
def merge(left, right):
i, j = 0, 0
res = []
while i < len(left) and j < len(right):
if left[i] <= right[j]:
res.append(left[i])
i+= 1
else:
res.append(right[j])
j += 1
res = res + left[i:] + right[j:]
return res
n = len(data)
if n <= 1:
return data
mid = n // 2
left = mergeSort(data[:mid])
right = mergeSort(data[mid:])
return merge(left, right)
arr = [23, 68, 1, 6, 10, 8, 99, 66]
print(f'结果:{mergeSort(arr)}')
'''
[23] [68] [23, 68]
[1] [6] [1, 6]
[23, 68] [1, 6] [1, 6, 23, 68]
[10] [8] [8, 10]
[99] [66] [66, 99]
[8, 10] [66, 99] [8, 10, 66, 99]
[1, 6, 23, 68] [8, 10, 66, 99] [1, 6, 8, 10, 23, 66, 68, 99]
结果:[1, 6, 8, 10, 23, 66, 68, 99]
'''2.5、堆排序:Heap Sort
不稳定排序,平均时间复杂度是O(nlogn),空间复杂度O(1)
堆是一个近似完全二叉树的结构
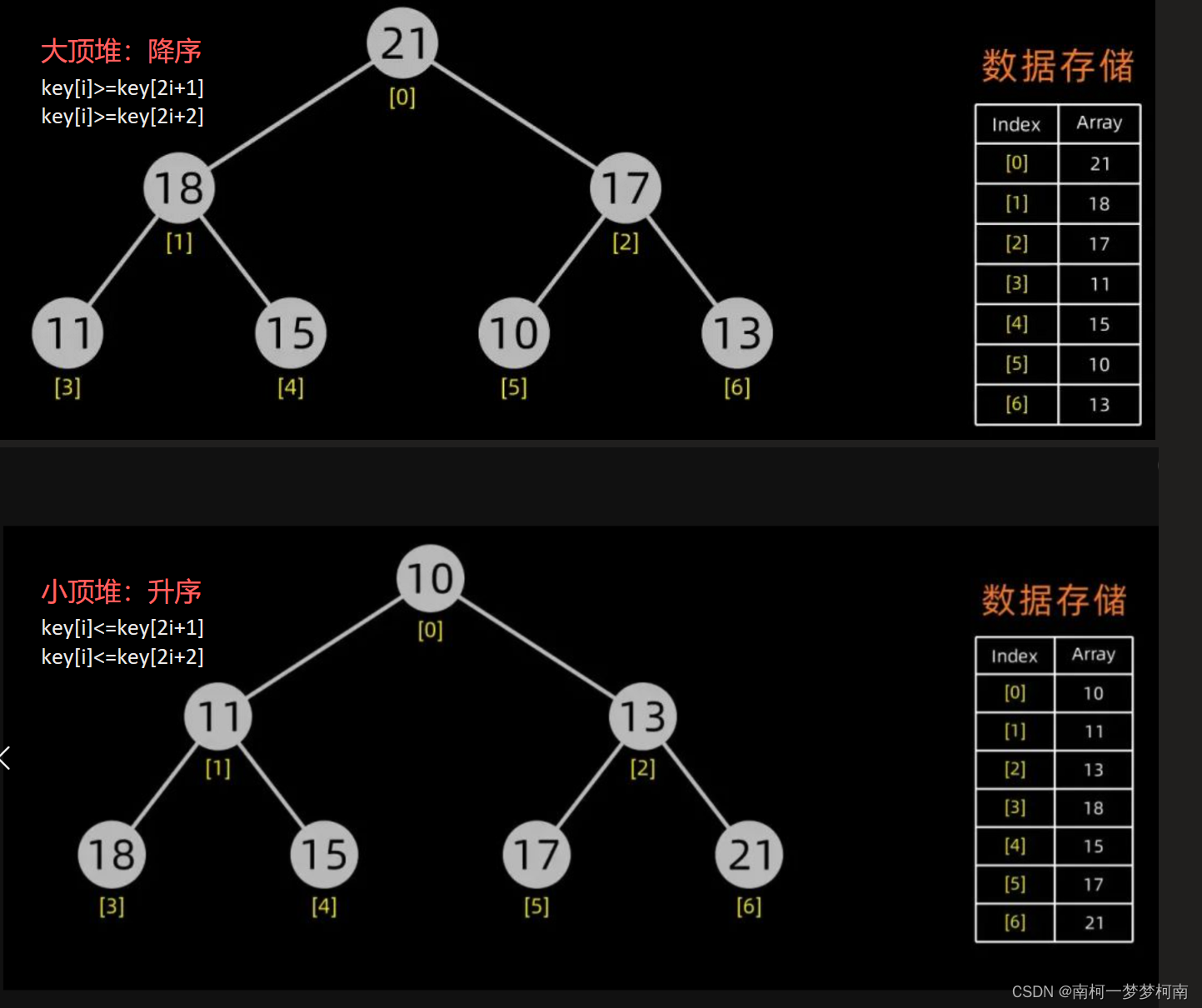
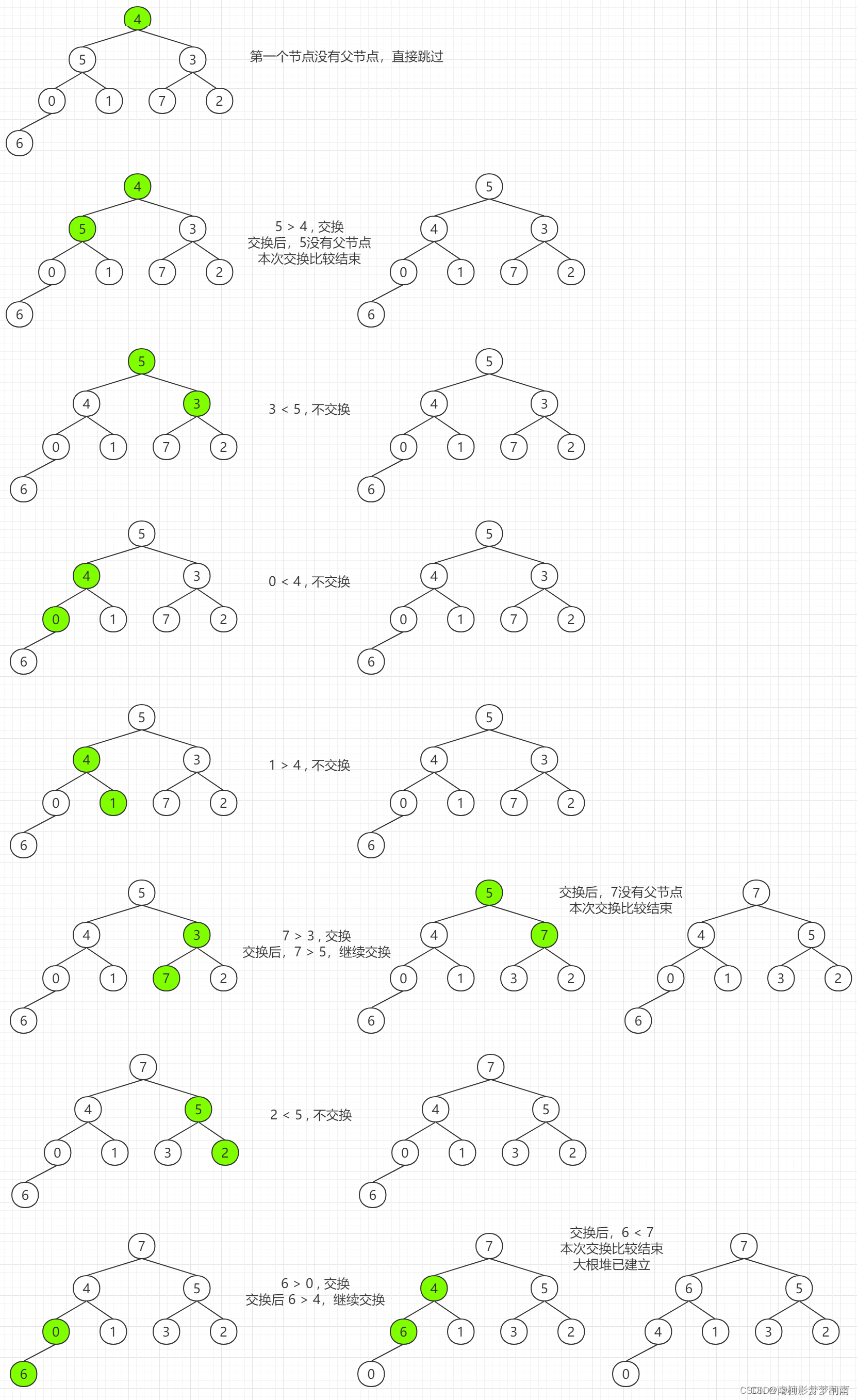
python
def heap_sort(nums):
def adjust_heap(i, end):
dad = i
son = 2*dad+1
while son < end:
if son+1 < end and nums[son+1] > nums[son]:
son = son + 1
if nums[dad] >= nums[son]:
return
nums[dad], nums[son] = nums[son], nums[dad]
dad = son
son = 2*dad+1
n = len(nums)
# 堆初始化,从最后一个非叶子节点创建大顶堆
for i in range(n//2-1,-1,-1):
adjust_heap(i, n)
print(nums)
# 输出堆顶元素后,剩余元素继续调整为堆
for i in range(n-1, 0, -1):
nums[0], nums[i] = nums[i], nums[0] # 每次最大的元素在根节点
adjust_heap(0, i) # 继续调整堆
return nums
arr = [23, 68, 1, 6, 10, 8, 99, 66]
res = heap_sort(arr)
print(res)
'''
[99, 68, 23, 66, 10, 8, 1, 6]
[1, 6, 8, 10, 23, 66, 68, 99]
'''2.6、希尔排序:Shell Sort
希尔排序:不稳定排序,时间复杂度O(n^(1.3~2)),空间复杂度O(1),是对时间上优化了的插入排序。
原理:
- 显示设定一个增量gap
- 对相距gap的元素进行插入排序
- 缩小增量
- 重复步骤2、3,直到gap不大于0
python
def shellSort(arr):
n = len(arr)
gap = 1
while gap < n/3:
gap = 3 * gap + 1
while gap > 0:
for i in range(gap, n):
tmp = arr[i]
j = i - gap
while j >= 0 and arr[j] > tmp:
arr[j+gap] = arr[j]
j -= gap
arr[j+gap] = tmp
gap = gap // 3
return arr
arr = [23, 68, 1, 6, 10, 8, 99, 66]
res = shellSort(arr)
print(res)
'''
gap=4
比较下标0,4 [10, 68, 1, 6, 23, 8, 99, 66]
比较下标1,5 [10, 8, 1, 6, 23, 68, 99, 66]
比较下标2,6 [10, 8, 1, 6, 23, 68, 99, 66]
比较下标3,7 [10, 8, 1, 6, 23, 68, 99, 66]
gap=1
比较下标0,1 [8, 10, 1, 6, 23, 68, 99, 66]
比较下标0,1,2 [1, 8, 10, 6, 23, 68, 99, 66]
比较下标0,1,2,3 [1, 6, 8, 10, 23, 68, 99, 66]
比较下标0,1,2,3,4,5,6,7 [1, 6, 8, 10, 23, 66, 68, 99]
[1, 6, 8, 10, 23, 66, 68, 99]
'''3、哈希
3.1、哈希算法
Hash表采用一个映射函数 f :key ---> address 将关键字映射到该记录在表中的存储位置,这种映射关系称作为Hash函数。
哈希表的效率非常高,查找、插入、删除操作只需要接近常量的时间即0(1)的时间级。如果需要在一秒种内查找上千条记录通常使用哈希表,哈希表的速度明显比树快,树的操作通常需要O(N)的时间级。哈希表不仅速度快,编程实现也相对容易。如果不需要遍历数据,不二的选择。
python中的hash其实就是dict
所谓的 hash 算法就是将字符串转换为数字的算法。通常有以下几种构造 Hash 函数的方法:
-
直接定址法:取关键字或者关键字的某个线性函数为 Hash 地址,即address(key) = a * key + b; 如知道学生的学号从2000开始,最大为4000,则可以将address(key)=key-2000(其中a = 1)作为Hash地址。
-
平方取中法:对关键字进行平方计算,取结果的中间几位作为 Hash 地址。如有以下关键字序列 {421,423,436} ,平方之后的结果为 {177241,178929,190096} ,那么可以取中间的两位数 {72,89,00} 作为 Hash 地址。
-
折叠法:将关键字拆分成几部分,然后将这几部分组合在一起,以特定的方式进行转化形成Hash地址。如图书的 ISBN 号为 8903-241-23,可以将 address(key)=89+03+24+12+3 作为 Hash 地址。
-
除留取余法:如果知道 Hash 表的最大长度为 m,可以取不大于m的最大质数 p,然后对关键字进行取余运算,address(key)=key % p。这里 p 的选取非常关键,p 选择的好的话,能够最大程度地减少冲突,p 一般取不大于m的最大质数。
3.2、示例
python
'''
问题:
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例:
strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
res = [["bat"],["nat","tan"],["ate","eat","tea"]]
分析:
nat tan 组成单词相同,所以是异位词
ate eat tea 组成单词相同,所以是异位词
解法:
哈希 + 排序
'''
class Solution(object):
def groupAnagrams(self, strs):
n = len(strs)
res = {} # key为字符串对应的数字,值为字符串列表
init = ord('a')
while n > 0:
str_tmp = strs.pop()
key = 0
key = ''.join(sorted(str_tmp))
if res.get(key) is None:
res[key] = [str_tmp]
else:
res[key].append(str_tmp)
n -= 1
return list(res.values())
print(Solution().groupAnagrams(["eat", "tea", "tan", "ate", "nat", "bat", "", ""]))
print(Solution().groupAnagrams(["ddddddddddg","dgggggggggg"]))
'''
[['', ''], ['bat'], ['nat', 'tan'], ['ate', 'tea', 'eat']]
[['dgggggggggg'], ['ddddddddddg']]
'''4、递归
4.1、递归
递归出口、自我调用、返回值
4.2、示例
外观数列


python
'''
使用递归 即由n-1的描得到n的描述
'''
class Solution(object):
def countAndSay(self, n):
# 结束条件
if n == 1:
return '1'
old_str = self.countAndSay(n-1) # 第n-1个描述
old_str_length = len(old_str)
new_str = ''
count = 1
for i in range(old_str_length-1):
if old_str[i] == old_str[i+1]:
count += 1
else:
new_str += str(count) + old_str[i]
count = 1
new_str += str(count) + old_str[-1]
return new_str
print(Solution().countAndSay(1))
print(Solution().countAndSay(2))
print(Solution().countAndSay(3))
print(Solution().countAndSay(4))
print(Solution().countAndSay(5))5、二分法查找
5.1、二分法
时间复杂度O(log n)
二分法也是头尾双指针法,滑动窗口是快慢双指针
二分法查找的序列必须是有序的,取序列中点将序列一分为二分别查找,每次缩小区间,因为每次将区间分为两份,所以次数为以2为底的n的对数,即O(log n)
5.2、示例
5.2.1、搜索旋转排序数组

python
'''
时间复杂度要求O(log n) 使用二分法查找
旋转数组也算是有序的,只需要判断mid在左半部分还是右半部分
nums = [4,5,6,7,0,1,2], target = 0
'''
class Solution:
def search(self, nums: list[int], target: int) -> int:
n = len(nums)
left = 0
right = n - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
if nums[mid] > nums[right]: # mid左边是有序数组
if nums[left] <= target <= nums[mid]:
right = mid - 1
else:
left = mid + 1
else: # mid右边是有序数组
if nums[mid] <= target <= nums[right]:
left = mid + 1
else:
right = mid - 1
return -15.2.2、搜索旋转排序数组Ⅱ
python
'''
给你 旋转后 的数组 nums 和一个整数 target
请你编写一个函数来判断给定的目标值是否存在于数组中
如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false
nums元素可重复
二分法查找
nums=[3,1,2,3,3,3,3],target=2
'''
class Solution:
def search(self, nums: list[int], target: int) -> bool:
n = len(nums)
left = 0
right = n - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return True
if nums[mid] < nums[right]: # mid右边序列有序
if nums[mid] <= target <= nums[right]:
left = mid + 1
else:
right = mid - 1
elif nums[mid] > nums[right]: # mid左边序列有序
if nums[left] <= target <= nums[mid]:
right = mid - 1
else:
left = mid + 1
else: # 重复元素
right -= 1
return False
print(Solution().search([2,5,6,0,0,1,2], 0)) # True
print(Solution().search([2,5,6,0,0,1,2], 3)) # False
print(Solution().search([1,0,1,1,1], 0)) # True
print(Solution().search([1,1,1,1,1,1,1,1,1,13,1,1,1,1,1,1,1,1,1,1,1,1], 13)) # True
print(Solution().search([3,1,2,3,3,3,3], 2)) # True5.2.3、寻找旋转排序数组中的最小值
python
'''
给你一个可能存在 重复 元素值的数组 nums
它原来是一个升序排列的数组,并按上述情形进行了多次旋转。
请你找出并返回数组中的 最小元素
'''
class Solution:
def findMin(self, nums: list[int]) -> int:
n = len(nums)
left = 0
right = n - 1
while left <= right:
mid = (left+right) // 2
# 需要判断旋转点是否为重复数字
if nums[mid] < nums[right]:
right = mid
elif nums[mid] > nums[right]:
left = mid + 1
else:
right -= 1
return nums[left]
res = Solution().findMin([1])
print(res)
res = Solution().findMin([1,2])
print(res)
res = Solution().findMin([2,1])
print(res)
res = Solution().findMin([3,1,3])
print(res)
res = Solution().findMin([3,1,2,3,3,3,3])
print(res)
res = Solution().findMin([4,5,6,7,0,1,4,4])
print(res)6、滑动窗口
6.1、滑动窗口
滑动窗口本质上是双指针同向移动(快慢指针),常用来解决字符串匹配问题。
核心思想:
- 初始化指针left和right,left=0,right=0
- 寻找可行解:不断扩大right,直到符合要求
- 优化可行解:不断增加left缩小窗口,直到窗口中的内容不再满足要求,更新结果
- 不断重复扩大窗口、缩小窗口,直到right到达终点
6.2、示例
6.2.1、最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串的长度。
遍历right,维护left
python
'''
滑动窗口
1、满足条件,即无重复,right右移
2、不满足条件,有重复,left右移直至无重复或left与right重合,right右移
简化一下:
1、如果不满足条件,left右移,直至无重复
2、right右移
3、记录结果
'''
class Solution(object):
def lengthOfLongestSubstring(self, s):
res = 0
left, right = 0, 0
for i in s:
while i in s[left: right]: # 不满足条件,left右移,直至无重复
left += 1
right += 1 # right右移
res = max(res, right-left) # 记录结果
return res
print(Solution().lengthOfLongestSubstring('abcabcbb')) # 3
print(Solution().lengthOfLongestSubstring('bbbbb')) # 1
print(Solution().lengthOfLongestSubstring('pwwkew')) # 36.2.2、最小覆盖子串
python
'''
滑动窗口+哈希表
1、不断增加right使滑动窗口增大,寻找可行解
2、不断增加left使滑动窗口缩小,优化可行解
'''
class Solution(object):
def minWindow(self, s, t):
t_dict={} # 哈希表记录各元素出现的次数
for c in t:
t_dict[c] = t_dict.get(c,0) + 1
len_dict = len(t_dict.keys())
valid = 0 # 记录t_dict不重复的元素有多少个
res=(0,float('inf'))
left=0
for right, item in enumerate(s):
if t_dict.get(item) is not None: # 更新t_dict和valid
t_dict[item] -= 1
if t_dict[item] == 0:
valid += 1
# 寻找可行解
if valid == len_dict:
# 优化可行解
while True:
left_item = s[left]
if left<=right and t_dict.get(left_item) is not None:
if t_dict[left_item] == 0:
break
t_dict[left_item] += 1
left += 1
# 记录可行解
if right-left < res[1]-res[0]:
res=(left, right)
# 记录之后继续缩小窗口
t_dict[left_item] += 1
left+=1
valid -= 1
if res[1] > len(s):
return ''
else:
return s[res[0]:res[1]+1]
print(Solution().minWindow('ADOBECODEBANC', 'ABC')) # BANC
print(Solution().minWindow('a', 'a')) # a
print(Solution().minWindow('a', 'aa')) # ''
print(Solution().minWindow('aabbbbbbbbbc', 'abc')) # abbbbbbbbbc6.2.3、串联所有单词的子串
python
'''
滑动窗口 + 哈希表
维护一个长度为len(words)*len(word[0])的滑动窗口
因为words中可能会有重复,需要哈希表来记录words中各单词出现的次数
s = "barfoothefoobarman", words = ["foo","bar"]
最后一次循环index+m*n=len_s 循环中要取到index=len_s-m*n 即range(0, len(s)-m*n+1)
'''
class Solution(object):
def findSubstring(self, s, words):
def sub_str(window, words_dict, n):
# 判断window是否是s的子串
for i in range(0, len(window), n):
word = window[i:i+n]
if words_dict.get(word): # 存在且不为0的情况下 次数-1
words_dict[word] -= 1
else:
return False
return True
words_dict = {}
for i in words:
words_dict[i] = words_dict.get(i, 0)+1
m = len(words)
n = len(words[0])
target_len = m*n
res = []
# left=i right=i+target_len-1
for i in range(len(s)-target_len+1):
window = s[i: i+target_len]
new_words_dict = words_dict.copy()
if sub_str(window, new_words_dict, n):
res.append(i)
return res
print(Solution().findSubstring('barfoothefoobarman', ["foo","bar"]))
print(Solution().findSubstring('wordgoodgoodgoodbestword', ["word","good","best","word"]))
print(Solution().findSubstring('barfoofoobarthefoobarman', ["bar","foo","the"]))
'''
[0, 9]
[]
[6, 9, 12]
'''7、回溯算法
7.1、回溯法
- 回溯法。回溯法被称为是万能的解法,几乎所有问题都可以用回溯法去解题。其核心思想就是枚举每一种情况,然后进行比较,最终得到最优解。这个算法的时间复杂度一般在指数级别O(2^n)。
- 动态规划。常用来求解可划分的问题。对于一个问题,它可以划分为由若干个子问题相互联系产生,那么就可以用动态规划来求解。
- 贪心。每次求得局部最优解,将局部最优解累加起来就变成了全局最优解。
- 问题。能够用动态规划和回溯法解答的题目都很有特点。一般来说就是多阶段,当前要求解的问题和其子问题有关,并且子问题的抉择影响到了后面的答案。如果当前问题规模记为f(n)的话,那么f(n)一定和f(n-1)或者f(n-2)有关系,可以是f(n)=f(n-1)+f(n-2),也可以是f(n)=max/min(f(n-1)+1,f(n-2))等等。具体要看问题描述。
回溯法是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为"回溯点"。
回溯法模板
python
result = []
def backtrack(选择列表, 路径):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
# 做选择
路径.add(选择)
将该选择从选择列表移除
backtrack(选择列表, 路径) # 核心 递归调用之前【做选择】,调用之后【撤销选择】
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表回溯算法能解决如下问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 棋盘问题:N皇后,解数独等等
7.2、示例
7.2.1、组合问题
1、组合求和

python
'''
回溯法
组合总和问题
一维数组用来存放符合条件的结果,二维数组用来存放结果集
'''
class Solution(object):
def combinationSum(self, candidates, target):
res = []
len_candidates = len(candidates)
def backtrace(path, start):
sum_res = sum(path)
# 回溯点
if sum_res == target:
res.append(path[:])
return
if sum_res > target:
return
for i in range(start, len_candidates):
path.append(candidates[i]) # 做选择
backtrace(path, i)
path.pop() # 回退
backtrace([], 0)
return res
print(Solution().combinationSum([2,3,6,7],7))
print(Solution().combinationSum([2,3,5],8))
print(Solution().combinationSum([2],1))
[[2, 2, 3], [7]]
[[2, 2, 2, 2], [2, 3, 3], [3, 5]]
[]2、组合总和II
python
'''
回溯法
组合总和问题
一维数组用来存放符合条件的结果,二维数组用来存放结果集
'''
class Solution(object):
def combinationSum(self, candidates, target):
res = []
candidates.sort()
len_candidates = len(candidates)
def backtrace(path, start):
sum_res = sum(path)
# 回溯点
if sum_res == target:
res.append(path[:])
return
if sum_res > target:
return
for i in range(start, len_candidates):
# 防止出现重复解, i>start是防止第一支重复解被减去,例如[1,1,6]的情况
if i > start and candidates[i] == candidates[i-1]:
continue
path.append(candidates[i]) # 做选择
backtrace(path, i+1)
path.pop() # 回退
backtrace([], 0)
return res
print(Solution().combinationSum([10,1,2,7,6,1,5],8))
print(Solution().combinationSum([2,5,2,1,2],5))
[[1, 1, 6], [1, 2, 5], [1, 7], [2, 6]]
[[1, 2, 2], [5]]7.2.2、全排列
python
'''
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
'''
class Solution(object):
def permute(self, nums):
n = len(nums)
res = []
def backtrace(path):
len_path = len(path)
# 回溯点
if len_path == n:
res.append(path[:])
return
for i in nums:
if i not in path:
# 做选择
path.append(i)
backtrace(path)
# 回退
path.pop()
backtrace([])
return res
print(Solution().permute([1,2,3]))
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]同一层的相同的元素只取一个,防止重复,通常使用标记法
python
'''
问题:给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
回溯法+标记法
nums中有重复数字,
如[1,1,2] 为方便区分记为[1_a,1_b,2]
访问的时候只有1_a被访问过,才能访问1_b
如果想要先访问1_b,再访问1_a,因为1_a未被标记过,不被允许
那么1_a和1_b就只能顺序访问,不能逆序访问,也就不会出现重复了
'''
class Solution:
def permuteUnique(self, nums):
n = len(nums)
nums.sort()
seen = [False] * n # 记录数字是否被访问过
res = []
def backtrace(path, seen):
if len(path) == n:
res.append(path[:])
return
for i in range(n):
if seen[i]:
continue
if i > 0 and nums[i] == nums[i-1] and seen[i-1] == False: # 层级之间只能顺序访问
continue
path.append(nums[i])
seen[i] = True
backtrace(path,seen)
path.pop()
seen[i]=False
backtrace([], seen)
return res
print(Solution().permuteUnique([1,1,2]))
print(Solution().permuteUnique([1,2,3]))
[[1, 1, 2], [1, 2, 1], [2, 1, 1]]
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]7.2.3、棋盘问题:解数独、N皇后
集合的交集:{1,2,3} & {1,3} = {1, 3}
集合的并集:{1,2,3} | {1,3,4} = {1, 2, 3, 4}
list没有这种用法


python
'''
题目数据保证了输入数独仅有一个解,而且是有效数独
回溯法
'''
class Solution(object):
def solveSudoku(self, board):
# 行、列、小的3*3的九宫格
rows = [set(str(i) for i in range(1,10)) for _ in range(9)]
cols = [set(str(i) for i in range(1,10)) for _ in range(9)]
palace = [[set(str(i) for i in range(1,10)) for _ in range(3)] for _ in range(3)]
nums = {'1', '2', '3', '4', '5', '6', '7', '8', '9'}
empty = [] # 记录空白位置(i,j)
# 统计行可用数字、列可用数字、快可用数字
for i in range(9):
for j in range(9):
item = board[i][j]
if item == '.':
empty.append((i,j))
else:
rows[i].remove(item)
cols[j].remove(item)
palace[i//3][j//3].remove(item)
empty_length = len(empty)
def backtrack(position):
# position 是第几个.
# 回溯点
if position < 0:
return True
i, j = empty[position]
for num in rows[i] & cols[j] & palace[i//3][j//3]:
# 保存现场
rows[i].remove(num)
cols[j].remove(num)
palace[i//3][j//3].remove(num)
# 做选择
board[i][j] = num
if backtrack(position - 1):
return True
# 恢复现场
rows[i].add(num)
cols[j].add(num)
palace[i//3][j//3].add(num)
return False
backtrack(empty_length-1)
board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
Solution().solveSudoku(board)
print(board)
[
['5', '3', '4', '6', '7', '8', '9', '1', '2'],
['6', '7', '2', '1', '9', '5', '3', '4', '8'],
['1', '9', '8', '3', '4', '2', '5', '6', '7'],
['8', '5', '9', '7', '6', '1', '4', '2', '3'],
['4', '2', '6', '8', '5', '3', '7', '9', '1'],
['7', '1', '3', '9', '2', '4', '8', '5', '6'],
['9', '6', '1', '5', '3', '7', '2', '8', '4'],
['2', '8', '7', '4', '1', '9', '6', '3', '5'],
['3', '4', '5', '2', '8', '6', '1', '7', '9']
]
python
'''
回溯法
一个4*4的n皇后格子坐标
(0,0) (0,1) (0,2) (0,3)
(1,0) (1,1) (1,2) (1,3)
(2,0) (2,1) (2,2) (2,3)
(3,0) (3,1) (3,2) (3,3)
规律:
左对角线i+j相等 0 1 2 3 4 5 6
右对角线i-j相等 -3 -2 -1 0 1 2 3
分析:
一行、一列、一条对角线都只能有一个皇后
用3个长度为n的list记录皇后的位置,举例[".Q..","...Q","Q...","..Q."]
行list i是坐标 j是皇后所在位置,最后结果为[1,3,0,2]
左对角线 i+j是坐标 1代表皇后 最后结果为 [0,1,1,0,1,1]
右对角线 i-j+(n-1)是坐标 1代表皇后 避免有负的坐标,最后结果为 [0,1,1,0,1,1,0]
遍历行 选中N皇后位置
时间复杂度O(n!)
...
'''
class Solution(object):
def solveNQueens(self, n):
res = []
rows = [None] * n
left = [0] * (2*n-1)
right = [0] * (2*n-1)
def backtrace(i):
# rows已经存进了n个列位置,构造成字符串形式
if None not in rows:
temp_res = []
for i in rows:
row = ['Q' if i==j else '.' for j in range(n)]
temp_res.append(''.join(row))
res.append(temp_res)
return
for j in range(n):
if j in rows: # 列已经被选中过了
continue
if left[i+j] == 1 : # 左对角线
continue
if right[i-j+(n-1)] == 1: # 右对角线
continue
rows[i], left[i+j], right[i-j+(n-1)] = j, 1, 1
backtrace(i+1)
rows[i], left[i+j], right[i-j+(n-1)] = None, 0, 0
backtrace(0)
return res
print(Solution().solveNQueens(4))
[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]8、BFS:宽度(广度)优先搜索
BFS:breadth first search
一层一层的搜索,一般使用队列(queue)实现,利用队列先进先出(FIFO)特性。
8.1、示例

8.2、BFS应用场景
层序遍历、最短路径
由于BFS的广度优先搜索特性,如果要找距离某一点的最短路径,最先搜索到满足条件的就是最短路径了。
bfs用到队列,可以使用collections中的deque
python
from collections import deque
import collections
d = deque([1,2,3])
print(d)
d.popleft()
print(d)
d.append(4)
print(d)
'''
deque([1, 2, 3])
deque([2, 3])
deque([2, 3, 4])
'''8.3、BFS代码实现
8.3.1、遍历示例图
python
def BFS(graph, start_point):
# graph代表图,start_point代表起点
queue = [] # 队列用于存放未访问过的点
queue.append(start_point)
finish_forEach = set() # 用于存放已经遍历过的点
finish_forEach.add(start_point)
# 循环遍历,直到队列为空,用pop(0)取出队首节点,然后判断节点连通的点是否被遍历过
while queue:
head_point = queue.pop(0)
nodes = graph[head_point]
for node in nodes:
if node not in finish_forEach:
queue.append(node)
finish_forEach.add(node)
print(head_point, end='->')
# 图
graph = {
'A': ['B', 'C'],
'B': ['A', 'C', 'D'],
'C': ['A', 'B', 'D', 'E'],
'D': ['B', 'C', 'E', 'F'],
'E': ['C', 'D'],
'F': ['D']
}
BFS(graph, 'A')
# A->B->C->D->E->F->8.3.2、示例图的两个节点间的最短路径
python
def BFS(graph, start_point):
queue = []
queue.append(start_point)
finish_forEach = set()
finish_forEach.add(start_point)
parent = {start_point: None} # 用于存放经过的路径
while queue:
head_point = queue.pop(0)
nodes = graph[head_point]
for node in nodes:
if node not in finish_forEach:
queue.append(node)
finish_forEach.add(node)
parent[node] = head_point
return parent
# 图
graph = {
'A': ['B', 'C'],
'B': ['A', 'C', 'D'],
'C': ['A', 'B', 'D', 'E'],
'D': ['B', 'C', 'E', 'F'],
'E': ['C', 'D'],
'F': ['D']
}
parent = BFS(graph, 'A')
print(parent) # {'A': None, 'B': 'A', 'C': 'A', 'D': 'B', 'E': 'C', 'F': 'D'}
end_point = 'F'
while end_point!= None:
print(end_point, end='')
end_point = parent[end_point]
# FDBA8.3.3、双向BFS运算数字华容道最少移动步数

移动数字改变1-8的数字排列到后图的情况,第一个图记为12345678.,第二个图记为123.46758,空格记为.,求最少经过多少步可以到达,如果无法到达,返回-1
找到.的位置上下左右移动,直到找到目标图。
1、单向的bfs
python
# 由当前字符串和移动方向获得移动后的字符串
# 如 cur_str=12345678. d=-3, next_str=12345.786
# 3*3的9宫格, 所以上下左右四个方向分别是.的下标加[-3, 3, -1, 1],注意防溢出,然后把两个位置的字符对调一下,就是新的字符串了
def get_next_str(cur_str, d):
index = cur_str.find('.')
next_index = index + d
next_str = ''
if 0<=next_index<9:
for i in range(9):
if i == index:
next_str += cur_str[next_index]
elif i == next_index:
next_str += cur_str[index]
else:
next_str += cur_str[i]
return next_str
def bfs(start_str, target_str):
dir = [-3, 3, -1, 1] # 上、下、左、右四个方向
queue = [start_str]
seen = set()
seen.add(start_str)
parent = {start_str: None} # 标记{子:父}结点关系
while queue:
cur_str = queue.pop(0)
if cur_str == target_str:
step = 0 # 使用了几步
end_point = target_str # 从最后一个结点开始查,它的父节点,父节点的父节点,直到初始位置
while end_point!=None:
step+=1
print(end_point, end='->')
end_point = parent[end_point]
print()
return step-1
for d in dir:
next_str = get_next_str(cur_str, d)
if next_str and next_str not in seen :
seen.add(next_str)
queue.append(next_str)
parent[next_str] = cur_str
return -1
start_str = '12345678.'
target_str = '123.46758'
res = bfs(start_str, target_str)
print(res)
'''
123.46758->1234.6758->1234567.8->12345678.->
3
'''2、双向bfs,就是图一和图二同时开始搜索,直到两者重合,步骤就是两者加到一起了
python
# 由当前字符串和移动方向获得移动后的字符串
# 如 cur_str=12345678. d=-3, next_str=12345.786
# 3*3的9宫格, 所以上下左右四个方向分别是.的下标加[-3, 3, -1, 1],注意防溢出,然后把两个位置的字符对调一下,就是新的字符串了
def get_next_str(cur_str, d):
index = cur_str.find('.')
next_index = index + d
next_str = ''
if 0<=next_index<9:
for i in range(9):
if i == index:
next_str += cur_str[next_index]
elif i == next_index:
next_str += cur_str[index]
else:
next_str += cur_str[i]
return next_str
def bfs(queue, seen1, seen2):
dir = [-3, 3, -1, 1] # 上、下、左、右四个方向
cur_str = queue.pop(0)
for d in dir:
next_str = get_next_str(cur_str, d)
if next_str in seen2:
return seen1[cur_str] + seen2[next_str] + 1
if next_str and next_str not in seen1 :
queue.append(next_str)
seen1[next_str] = seen1[cur_str] + 1
return -1
def main(start_str, target_str):
queue1 = [start_str]
queue2 = [target_str]
seen1 = {start_str: 0} # 去重+步数
seen2 = {target_str: 0}
while queue1 and queue2:
res = bfs(queue1, seen1, seen2) if len(queue1) < len(queue2) else bfs(queue2, seen2, seen1)
if res != -1:
return res
return -1
start_str = '12345678.'
target_str = '123.46758'
res = main(start_str, target_str)
print(res)
'''
3
'''3、双向bfs,输出路径和最小步数
python
# 由当前字符串和移动方向获得移动后的字符串
# 如 cur_str=12345678. d=-3, next_str=12345.786
# 3*3的9宫格, 所以上下左右四个方向分别是.的下标加[-3, 3, -1, 1],注意防溢出,然后把两个位置的字符对调一下,就是新的字符串了
def get_next_str(cur_str, d):
index = cur_str.find('.')
next_index = index + d
next_str = ''
if 0<=next_index<9:
for i in range(9):
if i == index:
next_str += cur_str[next_index]
elif i == next_index:
next_str += cur_str[index]
else:
next_str += cur_str[i]
return next_str
def bfs(queue, seen1, seen2, path):
dir = [-3, 3, -1, 1] # 上、下、左、右四个方向
cur_str = queue.pop(0)
for d in dir:
next_str = get_next_str(cur_str, d)
if next_str in seen2:
path[next_str] = cur_str
return seen1[cur_str] + seen2[next_str] + 1, next_str
if next_str and next_str not in seen1 :
queue.append(next_str)
seen1[next_str] = seen1[cur_str] + 1
path[next_str] = cur_str
return -1, ''
def main(start_str, target_str):
queue1 = [start_str]
queue2 = [target_str]
seen1 = {start_str: 0} # 去重+步数
seen2 = {target_str: 0}
path1 = {start_str: None}
path2 = {target_str: None}
while queue1 and queue2:
res, meet_str = bfs(queue1, seen1, seen2, path1) if len(queue1) < len(queue2) else bfs(queue2, seen2, seen1, path2)
if res != -1:
path_list1 = get_path(path1, meet_str)
path_list2 = get_path(path2, meet_str)
if meet_str in path_list1 and meet_str in path_list2:
path_list2.remove(meet_str)
path_list = path_list2[::-1] + path_list1
print('->'.join(path_list))
return res
return -1
def get_path(path, end_point):
path_list = []
while end_point!= None:
path_list.append(end_point)
end_point = path[end_point]
return path_list
start_str = '12345678.'
target_str = '123.46758'
res = main(start_str, target_str)
print(res)
'''
123.46758->1234.6758->1234567.8->12345678.
3
'''8.3.4、迷宫
下图给出了一个迷宫的平面图,其中标记为 11 的为障碍,标记为 00 的为可以通行的地方。

bash
01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000
python
data = '''
01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000
'''
# 将data转换为list [[...],[...],[...],...]
def get_graph(data):
graph = []
lines_list = data.split()
for line in lines_list:
line_list = []
for char in line:
line_list.append(int(char))
graph.append(line_list)
return graph
# i,j代表起始位置
def BFS(i, j):
graph = get_graph(data)
# D U L R 上下左右
direction = [[1,0,'D'],[-1,0,'U'],[0,-1,'L'],[0,1,'R']]
# 记录位置和路径
queue = [(i,j,'')]
seen = set()
while queue:
x, y, m = queue.pop(0)
print(x,y)
if 0<=x<len(graph) and 0<=y<len(graph[0]) and graph[x][y]==0 and (x,y) not in seen:
seen.add((x,y))
for dire in direction:
queue.append((x+dire[0], y+dire[1], m+dire[2]))
# 如果走到了终点,就是最短路径,直接返回
if x==len(graph)-1 and y==len(graph[0])-1:
return m
return -1
# 起点位置是0,0
print(BFS(0,0))
'''
DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRUUURRRRDDDDRDRRRRRURRRDRRDDDRRRRUURUUUUUUUULLLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR
'''8.3.5、转化数字的最小运算数

python
# 双搜
def bfs(queue, seen1, seen2, nums):
add = lambda x,y: x+y
sub = lambda x,y: x-y
xor = lambda x,y: x^y
ops = ['add','sub','xor']
x = queue.pop(0)
for num in nums:
for op in ops:
next_start = eval(op)(x,num)
if next_start in seen2:
return seen1[x] + seen2[next_start] + 1
if 0<=next_start<=1000 and next_start not in seen1:
queue.append(next_start)
seen1[next_start] = seen1[x] + 1
return -1
def main(nums, start, goal):
queue1 = [start]
queue2 = [goal]
visited1 = {start: 0}
visited2 = {goal: 0}
# 选择较短的队列进行bfs
while queue1 and queue2:
if len(queue1) < len(queue2):
res = bfs(queue1,visited1,visited2,nums)
else:
res = bfs(queue2,visited2,visited1,nums)
if res != -1: # 代表找到了res
return res
return -1
nums = [3,5,7]
start = 0
goal = -4
res = main(nums, start, goal)
print(res)
# 2
# 0+3=3 3-7=-48.3.6、单词接龙Ⅱ
python
'''
bfs
这里使用的是字典来记录路径
'''
class Solution:
def findLadders(self, beginWord, endWord, wordList):
n = len(beginWord)
wordList.append(beginWord)
words_dict = {} # 为方便查找下一个单词的位置,将wordList整理成{'*ot': ['hot', 'dot', 'lot']}的形式
for word in wordList:
for i in range(n):
key = word[:i] + '*' + word[i+1:]
value = words_dict.get(key) if words_dict.get(key) else []
value.append(word)
words_dict[key] = value
parent = {} # 记录路径
seen = set() # 记录已访问单词
queue = [beginWord]
while queue :
flag = False
size = len(queue )
tmp = []
print('queue ', queue )
for _ in range(size): # 分层遍历
word = queue.pop(0)
seen.add(word)
for i in range(n):
match = word[:i] + '*' + word[i+1:]
for new_word in words_dict[match] :
if new_word in seen or new_word in queue : # 这里不能是seen也不能是queue ,因为queue 是本层待遍历,new_word是下一层
continue
tmp.append(new_word)
if word not in parent.get(new_word, []):
parent[new_word] = parent.get(new_word, []) + [word]
if new_word == endWord:
flag = True
if flag:
break
queue = tmp
print('parent', parent)
res = [[endWord]]
while res[0][0] != beginWord:
# 或者直接用推导式
res = [[w] + key for key in res for w in parent[key[0]]]
tmp = []
# for key in res:
# for w in parent[key[0]]: # key[0]是因为我们每次都把新单词插入头部[w] + key
# tmp.append([w] + key)
# res = tmp
print('res',res)
return res
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log","cog"]
res = Solution().findLadders(beginWord, endWord, wordList)
'''
queue ['hit']
queue ['hot']
queue ['dot', 'lot']
queue ['dog', 'log']
parent {'hot': ['hit'], 'dot': ['hot'], 'lot': ['hot'], 'dog': ['dot'], 'log': ['lot'], 'cog': ['dog', 'log']}
res [['hit', 'hot', 'dot', 'dog', 'cog'], ['hit', 'hot', 'lot', 'log', 'cog']]
======== [['hit', 'hot', 'dot', 'dog', 'cog'], ['hit', 'hot', 'lot', 'log', 'cog']]
'''
'''
bfs
还可以在queue 里面记录路径,queue 的最后一个元素用来遍历,[:-1]用来记录路径
这种方法空间占用会比较多
'''
class Solution:
def findLadders(self, beginWord, endWord, wordList):
res = []
n = len(beginWord)
wordList.append(beginWord)
words_dict = {} # 为方便查找下一个单词的位置,将wordList整理成{'*ot': ['hot', 'dot', 'lot']}的形式
for word in wordList:
for i in range(n):
key = word[:i] + '*' + word[i+1:]
value = words_dict.get(key) if words_dict.get(key) else []
value.append(word)
words_dict[key] = value
seen = set() # 记录已访问单词
queue = [[beginWord]]
while queue :
flag = False
size = len(queue)
tmp = []
print('queue ', queue )
for w in queue : # 先把本层都标记一下,防止new_word和本层内容重复
seen.add(w[-1])
for _ in range(size): # 分层遍历
words = queue.pop(0)
word = words[-1]
seen.add(word)
for i in range(n):
match = word[:i] + '*' + word[i+1:]
for new_word in words_dict[match] :
if new_word in seen:
continue
tmp.append(words + [new_word])
if new_word == endWord:
flag = True
queue = tmp
if flag:
res = queue[:]
break
print('res',res)
return res
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log","cog"]
res = Solution().findLadders(beginWord, endWord, wordList)
'''
queue [['hit']]
queue [['hit', 'hot']]
queue [['hit', 'hot', 'dot'], ['hit', 'hot', 'lot']]
queue [['hit', 'hot', 'dot', 'dog'], ['hit', 'hot', 'lot', 'log']]
res [['hit', 'hot', 'dot', 'dog', 'cog'], ['hit', 'hot', 'lot', 'log', 'cog']]
'''
python
# 找最短路径,用bfs
# 双向bfs
from collections import defaultdict, deque
class Solution(object):
def ladderLength(self, beginWord, endWord, wordList):
"""
:type beginWord: str
:type endWord: str
:type wordList: List[str]
:rtype: int
"""
if endWord not in wordList:
return 0
n = len(beginWord)
word_dict = defaultdict(list)
for w in wordList:
for i in range(n):
key = w[:i] + '*' + w[i+1:]
word_dict[key] += [w]
def bfs(queue, seen1, seen2):
size = len(queue)
tmp = []
for _ in range(size):
word = queue.popleft()
if word in seen2: # seen1和seen2相遇代表遍历完成
return False
for i in range(n):
key = word[:i] + '*' + word[i+1:]
for next_word in word_dict[key]:
if next_word in seen1:
continue
tmp.append(next_word)
seen1.add(word)
queue.extend(tmp)
return True
# 双向bfs
# 从左向右找
queue_left = deque()
queue_left.append(beginWord)
seen_left = set()
seen_left.add(beginWord)
# 从右向左找
queue_right = deque()
queue_right.append(endWord)
seen_right = set()
seen_right.add(endWord)
# bfs 选队列短的进行bfs,直到两者重合
res_left = 0
res_right = 0
res = 0
while queue_left and queue_right:
flag = True
if len(queue_left) <= len(queue_right):
flag = bfs(queue_left, seen_left, seen_right)
res_left += 1
else:
flag = bfs(queue_right, seen_right, seen_left)
res_right += 1
if flag is False: # 找到了结果,结束
break
else: # 如果始终没有找到最短路径,把层高置0
return 0
if res_left and res_right:
return res_left + res_right - 1
else:
return res_left+res_right
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log","cog"]
res = Solution().ladderLength(beginWord, endWord, wordList)
print(res) # 5
beginWord = "hot"
endWord = "dot"
wordList = ["hot","dog","dot"]
res = Solution().ladderLength(beginWord, endWord, wordList)
print(res) # 2
beginWord = "hot"
endWord = "dog"
wordList = ["hot","dog","dot"]
res = Solution().ladderLength(beginWord, endWord, wordList)
print(res) # 39、DFS:深度优先搜索
DFS:depth first search
9.1、示例
对每一个可能的分支路径深入到不能再深入
对于同一个树或图,DFS序不一定唯一
优先使用栈(stack)来实现,利用栈的先进后出特性

9.2、应用场景
求子序列、求子集
找所有可能的解决方案
9.3、代码实现
9.3.1、遍历示例图
python
graph = {
"A": ["B", "C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D", "E"],
"D": ["B", "C", "E", "F"],
"E": ["C", "D"],
"F": ["D"]
}
# graph: 图 s: 图的起点
def BFS(graph, s):
stack = [s] # 创建一个数组作为栈,用于存储待访问的节点
seen = {s} # 创建一个集合,用于存放已访问过的点
while stack:
current = stack.pop() # 通过queue.pop()读取栈最后一个
print(current, end= ' ')
nodes = graph[current] # 读取每个点相邻的点
# 判重:循环判断相邻的点是否读过
for w in nodes:
if w not in seen:
stack.append(w)
seen.add(w)
BFS(graph, "A")
'''
A C E D F B
'''9.3.2、玩具蛇

python
'''
第一个格子为起点,可以有1-16个数字,记为num
以这个格子为中心向上下左右四个方向发散,可以放num+1或num-1
注意边界条件
queue为[(i,j,{(i,j):num})]
字典里面用来存储路径,经过16个坐标的时候就得到了一个结果,
去重因为要考虑坐标和数字,seen不好做处理,所以用路径的key和value代替seen进行去重操作
最后结果是104
'''
class Solution:
def dfs(self):
nums = [i+1 for i in range(16)]
dirs = [(0,1),(0,-1),(1,0),(-1,0)]
res = []
for num in nums:
queue = [(0,0,{(0,0):num})]
while queue:
i,j,path_dict = queue.pop()
cur_num = path_dict[(i,j)]
if len(path_dict) == 16:
res.append(path_dict.copy())
continue
next_nums = []
if 1<=cur_num+1<=16 and cur_num+1 not in path_dict.values():
next_nums.append(cur_num+1)
if 1<=cur_num-1<=16 and cur_num-1 not in path_dict.values():
next_nums.append(cur_num-1)
if not next_nums:
continue
for di,dj in dirs:
if not (0<=i+di<4 and 0<=j+dj<4):
continue
for next_num in next_nums:
if (i+di,j+dj) not in path_dict.keys():
queue.append((i+di,j+dj,{**path_dict,(i+di,j+dj):next_num}))
return res
obj = Solution()
res = obj.dfs()
for r in res:
for i in range(4):
for j in range(4):
print(f"{r[i,j]:^4}",end=' ')
print()
print('*'*20)
print(len(res))
'''
1 8 9 16
2 7 10 15
3 6 11 14
4 5 12 13
********************
1 8 9 10
2 7 16 11
3 6 15 12
4 5 14 13
********************
1 8 9 10
2 7 12 11
3 6 13 16
4 5 14 15
********************
1 8 9 10
2 7 12 11
3 6 13 14
4 5 16 15
********************
1 16 15 14
2 7 8 13
3 6 9 12
4 5 10 11
********************
1 10 11 12
2 9 8 13
3 6 7 14
4 5 16 15
********************
1 16 13 12
2 15 14 11
3 6 7 10
4 5 8 9
********************
1 14 13 12
2 15 16 11
3 6 7 10
4 5 8 9
********************
1 14 15 16
2 13 12 11
3 6 7 10
4 5 8 9
********************
1 16 11 10
2 15 12 9
3 14 13 8
4 5 6 7
********************
1 12 11 10
2 13 16 9
3 14 15 8
4 5 6 7
********************
1 12 11 10
2 13 14 9
3 16 15 8
4 5 6 7
********************
1 14 15 16
2 13 10 9
3 12 11 8
4 5 6 7
********************
1 14 13 12
2 15 10 11
3 16 9 8
4 5 6 7
********************
1 12 13 16
2 11 14 15
3 10 9 8
4 5 6 7
********************
1 12 13 14
2 11 16 15
3 10 9 8
4 5 6 7
********************
1 16 15 14
2 11 12 13
3 10 9 8
4 5 6 7
********************
1 6 7 8
2 5 10 9
3 4 11 12
16 15 14 13
********************
1 8 9 10
2 7 6 11
3 4 5 12
16 15 14 13
********************
1 4 5 16
2 3 6 15
9 8 7 14
10 11 12 13
********************
1 4 5 6
2 3 16 7
13 14 15 8
12 11 10 9
********************
1 4 5 6
2 3 8 7
11 10 9 16
12 13 14 15
********************
1 4 5 6
2 3 8 7
15 14 9 10
16 13 12 11
********************
1 4 5 6
2 3 8 7
15 16 9 10
14 13 12 11
********************
1 16 15 14
2 3 12 13
5 4 11 10
6 7 8 9
********************
1 16 15 14
2 3 4 13
7 6 5 12
8 9 10 11
********************
1 2 7 8
16 3 6 9
15 4 5 10
14 13 12 11
********************
1 2 11 12
4 3 10 13
5 8 9 14
6 7 16 15
********************
1 2 15 14
4 3 16 13
5 8 9 12
6 7 10 11
********************
1 2 15 16
4 3 14 13
5 8 9 12
6 7 10 11
********************
1 2 13 12
4 3 14 11
5 16 15 10
6 7 8 9
********************
1 2 9 10
4 3 8 11
5 6 7 12
16 15 14 13
********************
1 2 5 6
16 3 4 7
15 12 11 8
14 13 10 9
********************
1 2 3 16
8 7 4 15
9 6 5 14
10 11 12 13
********************
1 2 3 16
6 5 4 15
7 10 11 14
8 9 12 13
********************
1 2 3 4
16 11 10 5
15 12 9 6
14 13 8 7
********************
1 2 3 4
12 11 10 5
13 16 9 6
14 15 8 7
********************
1 2 3 4
12 11 10 5
13 14 9 6
16 15 8 7
********************
1 2 3 4
14 15 16 5
13 10 9 6
12 11 8 7
********************
1 2 3 4
14 13 12 5
15 10 11 6
16 9 8 7
********************
1 2 3 4
12 13 16 5
11 14 15 6
10 9 8 7
********************
1 2 3 4
12 13 14 5
11 16 15 6
10 9 8 7
********************
1 2 3 4
16 15 14 5
11 12 13 6
10 9 8 7
********************
1 2 3 4
10 9 6 5
11 8 7 16
12 13 14 15
********************
1 2 3 4
14 13 6 5
15 12 7 8
16 11 10 9
********************
1 2 3 4
14 15 6 5
13 16 7 8
12 11 10 9
********************
1 2 3 4
16 15 6 5
13 14 7 8
12 11 10 9
********************
1 2 3 4
16 7 6 5
15 8 9 10
14 13 12 11
********************
1 2 3 4
8 7 6 5
9 12 13 16
10 11 14 15
********************
1 2 3 4
8 7 6 5
9 12 13 14
10 11 16 15
********************
1 2 3 4
8 7 6 5
9 16 15 14
10 11 12 13
********************
1 2 3 4
8 7 6 5
9 10 11 12
16 15 14 13
********************
16 9 8 1
15 10 7 2
14 11 6 3
13 12 5 4
********************
16 9 8 7
15 10 1 6
14 11 2 5
13 12 3 4
********************
16 9 8 7
15 10 5 6
14 11 4 1
13 12 3 2
********************
16 9 8 7
15 10 5 6
14 11 4 3
13 12 1 2
********************
16 1 2 3
15 10 9 4
14 11 8 5
13 12 7 6
********************
16 7 6 5
15 8 9 4
14 11 10 3
13 12 1 2
********************
16 1 4 5
15 2 3 6
14 11 10 7
13 12 9 8
********************
16 3 4 5
15 2 1 6
14 11 10 7
13 12 9 8
********************
16 3 2 1
15 4 5 6
14 11 10 7
13 12 9 8
********************
16 1 6 7
15 2 5 8
14 3 4 9
13 12 11 10
********************
16 5 6 7
15 4 1 8
14 3 2 9
13 12 11 10
********************
16 5 6 7
15 4 3 8
14 1 2 9
13 12 11 10
********************
16 3 2 1
15 4 7 8
14 5 6 9
13 12 11 10
********************
16 3 4 5
15 2 7 6
14 1 8 9
13 12 11 10
********************
16 5 4 1
15 6 3 2
14 7 8 9
13 12 11 10
********************
16 5 4 3
15 6 1 2
14 7 8 9
13 12 11 10
********************
16 1 2 3
15 6 5 4
14 7 8 9
13 12 11 10
********************
16 11 10 9
15 12 7 8
14 13 6 5
1 2 3 4
********************
16 9 8 7
15 10 11 6
14 13 12 5
1 2 3 4
********************
16 13 12 1
15 14 11 2
8 9 10 3
7 6 5 4
********************
16 13 12 11
15 14 1 10
4 3 2 9
5 6 7 8
********************
16 13 12 11
15 14 9 10
6 7 8 1
5 4 3 2
********************
16 13 12 11
15 14 9 10
2 3 8 7
1 4 5 6
********************
16 13 12 11
15 14 9 10
2 1 8 7
3 4 5 6
********************
16 1 2 3
15 14 5 4
12 13 6 7
11 10 9 8
********************
16 1 2 3
15 14 13 4
10 11 12 5
9 8 7 6
********************
16 15 10 9
1 14 11 8
2 13 12 7
3 4 5 6
********************
16 15 6 5
13 14 7 4
12 9 8 3
11 10 1 2
********************
16 15 2 3
13 14 1 4
12 9 8 5
11 10 7 6
********************
16 15 2 1
13 14 3 4
12 9 8 5
11 10 7 6
********************
16 15 4 5
13 14 3 6
12 1 2 7
11 10 9 8
********************
16 15 8 7
13 14 9 6
12 11 10 5
1 2 3 4
********************
16 15 12 11
1 14 13 10
2 5 6 9
3 4 7 8
********************
16 15 14 1
9 10 13 2
8 11 12 3
7 6 5 4
********************
16 15 14 1
11 12 13 2
10 7 6 3
9 8 5 4
********************
16 15 14 13
1 6 7 12
2 5 8 11
3 4 9 10
********************
16 15 14 13
5 6 7 12
4 1 8 11
3 2 9 10
********************
16 15 14 13
5 6 7 12
4 3 8 11
1 2 9 10
********************
16 15 14 13
3 2 1 12
4 7 8 11
5 6 9 10
********************
16 15 14 13
3 4 5 12
2 7 6 11
1 8 9 10
********************
16 15 14 13
5 4 1 12
6 3 2 11
7 8 9 10
********************
16 15 14 13
5 4 3 12
6 1 2 11
7 8 9 10
********************
16 15 14 13
1 2 3 12
6 5 4 11
7 8 9 10
********************
16 15 14 13
7 8 11 12
6 9 10 1
5 4 3 2
********************
16 15 14 13
3 4 11 12
2 5 10 9
1 6 7 8
********************
16 15 14 13
3 2 11 12
4 1 10 9
5 6 7 8
********************
16 15 14 13
1 2 11 12
4 3 10 9
5 6 7 8
********************
16 15 14 13
1 10 11 12
2 9 8 7
3 4 5 6
********************
16 15 14 13
9 10 11 12
8 5 4 1
7 6 3 2
********************
16 15 14 13
9 10 11 12
8 5 4 3
7 6 1 2
********************
16 15 14 13
9 10 11 12
8 1 2 3
7 6 5 4
********************
16 15 14 13
9 10 11 12
8 7 6 5
1 2 3 4
********************
104
'''10、动态规划
10.1、动态规划
动态规划:把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划算法常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
动态规划算法一般可以分为以下四个步骤:
- 找出最优解的性质,并刻划其结构特征
- 递归地定义最优值
- 以自底向上的方式计算出最优值
- 根据计算最优值时得到的信息,构造最优解
可用于以下问题:
- 0/1背包问题
- 数塔问题
- 矩阵连乘问题
- 最长公共子序列
- 最优二叉查找树
- 多段图的最短路径问题
- 斐波那契数列
- 等等
10.2、示例
10.2.1、斐波那契数列
python
# F(0)=1 F(1)=1 F(n)=F(n-1)+F(n-2) (n>=2)
def fib(n):
if n==0: return 1
last = 0
current = 1
for i in range(1, n+1):
last, current = current, last + current
return current10.2.2、正则表达式匹配
python
'''
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
f[i][j] 就记录s的前i个和p的前j个字符是否匹配
用f[0][0]=True表示两个空字符s='' p=''可以匹配
'''
class Solution:
def isMatch(self, s, p):
len_s, len_p = len(s), len(p)
s = ' ' + s
p = ' ' + p
f = [ [False]*(len_p+1) for _ in range(len_s+1) ]
f[0][0] = True
i,j=0,0
for j in range(2, len_p + 1):
if p[j] == "*":
f[0][j] = f[0][j-2]
for i in range(1, len_s+1):
for j in range(1, len_p+1):
if p[j] != '*':
if s[i] == p[j] or p[j] == '.':
f[i][j] = f[i-1][j-1]
else:
if s[i] == p[j-1] or p[j-1] == '.':
f[i][j] = f[i-1][j] or f[i][j-2]
else:
f[i][j] = f[i][j-2]
return f[len_s][len_p]
print(Solution().isMatch("aa", "a"))
print(Solution().isMatch("aa", "a*"))
print(Solution().isMatch("ab", ".*"))
False
True
True
python
'''
给你一个输入字符串 (s) 和一个字符模式 (p) ,请你实现一个支持 '?' 和 '*' 匹配规则的通配符匹配:
'?' 可以匹配任何单个字符。
'*' 可以匹配任意字符序列(包括空字符序列)。
判定匹配成功的充要条件是:字符模式必须能够 完全匹配 输入字符串(而不是部分匹配)。
同样使用动态规划dp[i][j]
'''
class Solution(object):
def isMatch(self, s, p):
m, n = len(s), len(p)
dp = [ [False]*(n+1) for _ in range(m+1) ]
s = ' ' + s
p = ' ' + p
# 边界条件
dp[0][0] = True
for j in range(1, n+1):
if p[j] == '*':
dp[0][j] = dp[0][j-1]
# 递归
for i in range(1, m+1):
for j in range(1, n+1):
if p[j] == '*':
dp[i][j] = dp[i][j-1] or dp[i-1][j]
elif p[j] == '?' or s[i] == p[j]:
dp[i][j] = dp[i-1][j-1]
return dp[m][n]
print(Solution().isMatch("aa", "a"))
print(Solution().isMatch("aa", "*"))
print(Solution().isMatch("abcbefg", "ab*fg"))
print(Solution().isMatch("abcbefg", "ab*cg"))
False
True
True
False10.2.3、最大子数组和
python
'''
问题:
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
算法:
动态规划
分析:
dp[i]代表前i个元素中连续子数组的最大和
如果dp[i-1]<0, dp[i]=+nums[i]
dp[i-1]>=0, dp[i]=dp[i-1]+nums[i]
'''
class Solution(object):
def maxSubArray(self, nums):
n = len(nums)
dp = [nums[0]] * n
dp[0] = nums[0]
for i in range(1,n):
if dp[i-1] < 0:
dp[i] = nums[i]
else:
dp[i] = dp[i-1] + nums[i]
res = max(dp)
return res
print(Solution().maxSubArray([-2,1,-3,4,-1,2,1,-5,4]))
print(Solution().maxSubArray([5,4,-1,7,8]))
6
2310.2.4、不同路径
python
'''
动态规划法
dp[i][j] 从(0,0)走到(i,j)的路径个数
只能向右向下移动,所以
dp[i][j] = dp[i-1][j] + dp[i][j-1]
边界条件:
dp[0][0] = 1
dp[1][0] = 1
dp[2][0] = 1
...
dp[m-1][0] = 1
dp[0][1] = 1
dp[0][2] = 1
...
dp[0][n] = 1
'''
class Solution(object):
def uniquePaths(self, m, n):
dp = [[0]*n for _ in range(m)]
for i in range(m):
dp[i][0] = 1
for j in range(n):
dp[0][j] = 1
for i in range(1,m):
for j in range(1,n):
dp[i][j] = dp[i][j-1] + dp[i-1][j]
return dp[m-1][n-1]
print(Solution().uniquePaths(3,7)) # 28
print(Solution().uniquePaths(3,3)) # 610.2.5、不同的子序列
python
'''
字符串匹配问题:滑动窗口、动态规划
dp[i][j]: s t长度大于1,不必考虑空字符串了,s[:i]中t[:j]出现的子序列个数
若i<j, dp[i][j] = 0
s[0]==t[0], dp[0][0]=1
s[0]!=t[0], dp[0][0]=0
i>0,
if s[i] == t[j]:
dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
else:
dp[i][j] = dp[i-1][j]
s = babgbag
t = bag
b a g
b 1 0 0
a 1 1 0
b 2 1 0
g 2 1 1
b 3 1 1
a 3 4 1
g 3 4 5
'''
class Solution(object):
def numDistinct(self, s, t):
"""
:type s: str
:type t: str
:rtype: int
"""
m = len(s)
n = len(t)
dp = [[0]*n for _ in range(m)]
dp[0][0] = 1 if s[0] == t[0] else 0
# 边界值
for i in range(1, m):
if s[i] == t[0]:
dp[i][0] = dp[i-1][0] + 1
else:
dp[i][0] = dp[i-1][0]
for j in range(1,n):
dp[0][j] = 0
# 遍历
for i in range(1,m):
for j in range(1,n):
if j > i:
continue
if s[i] == t[j]:
dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
else:
dp[i][j] = dp[i-1][j]
return dp[-1][-1]
print(Solution().numDistinct(s = "rabbbit", t = "rabbit")) # 3
print(Solution().numDistinct(s = "babgbag", t = "bag")) # 511、贪心算法
11.1、贪心算法
贪心算法,又称贪婪算法、登山算法,根本思想是逐步到达山顶,即逐步获得最优解,是解决最优化问题时的一种简单但是适用范围有限的策略。
虽然贪心算法不能对所有问题都得到整体最优解,但在一些情况下,即使贪心算法不一定能得到整体最优解,其最终结果却是最优解的很好近似
用贪心算法求解问题要满足以下条件:
- 贪心选择性:所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到(这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别)
- 最有子结构性质:当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质
贪心算法与动态规划的差别:
-
相同:贪心算法和动态规划算法都要求问题具有最优子结构性质
-
不同:动态规划算法通常以自底向上 的方式解各子问题,初始值--dp(1) --dp(2)......dp(n);而贪心算法则通常以自顶向下 的方式进行(倒推),以迭代的方式作出相继的贪心选择---即每作一次贪心选择就将所求问题简化为规模更小的子问题
贪心算法常用来解决
- 找零问题
- 背包问题
- 买卖股票的最佳时机
- 哈夫曼编码
- 最小生成树-prim算法
- 单源最短路径-Dijkstra算法
- 等等
11.2、示例
11.2.1、跳跃游戏
python
'''
贪心
尽可能每次都跳到最远
从右向左查找上一个位置
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
提示:
1 <= nums.length <= 104
0 <= nums[i] <= 1000
题目保证可以到达 nums[n-1]
'''
class Solution:
def jump(self, nums):
n = len(nums)
position = n-1
step = 0
while position > 0:
for i in range(n):
if i + nums[i] >= position:
position = i
step += 1
break
return step
print(Solution().jump([2,3,1,1,4]))
print(Solution().jump([2,3,0,1,4]))
2
211.2.2、买卖股票的最佳时机
python
'''
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票
贪心算法
'''
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
# 买入之后手里的钱 卖出之后手里的钱
buy, sell = -float('inf'), 0
for p in prices:
buy = max(buy, 0-p)
sell = max(sell, buy+p)
return sell
print(Solution().maxProfit([7,1,5,3,6,4])) # 5
python
'''
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
贪心算法
'''
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
# 买入之后手里的钱 卖出之后手里的钱
buy, sell = -float('inf'), 0
for p in prices:
buy = max(buy, sell-p)
sell = max(sell, buy+p)
return sell
print(Solution().maxProfit([7,1,5,3,6,4])) # 7
python
'''
最多可以完成 两笔 交易
贪心算法
'''
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
# 买入之后手里的钱 卖出之后手里的钱
buy1, sell1 = -float('inf'), 0 # 第一次交易
buy2, sell2 = -float('inf'), 0 # 第二次交易
for p in prices:
# 第一次交易
buy1 = max(buy1, 0-p)
sell1 = max(sell1, buy1+p)
# 第二次交易
buy2 = max(buy2, sell1-p)
sell2 = max(sell2, buy2+p)
return sell2
print(Solution().maxProfit(prices = [3,3,5,0,0,3,1,4])) # 611.2.3、加油站
python
'''
贪心
总油量<总消耗,一定无解
总油量>=总消耗,一定有解,题目保证唯一解
让车从i出发,rest大于0都可以到达
如果rest[j]<0
说明 rest[i],rest[i+1],...rest[j-1] >=0
rest[j] < 0
此时从 i+1,i+2,...,j-1 出发的车也都无法到达j
汽车只需贪心的从j+1重新出发
'''
class Solution(object):
def canCompleteCircuit(self, gas, cost):
"""
:type gas: List[int]
:type cost: List[int]
:rtype: int
"""
# 总油量<总消耗,一定无解
if sum(gas) < sum(cost):
return -1
n = len(gas)
start_index = 0 # 汽车出发的位置
rest = 0 # 汽车剩余油量
for i in range(n):
rest += gas[i]-cost[i]
if rest < 0: # # 在i处的油量<0,说明从之前站点出发的车均无法到达i
start_index = i+1
rest = 0
return start_index
gas = [1,2,3,4,5]
cost = [3,4,5,1,2]
print(Solution().canCompleteCircuit(gas,cost)) # 311.2.4、分发糖果
python
'''
贪心
每个孩子至少分配到 1 个糖果。
相邻两个孩子评分更高的孩子会获得更多的糖果。
先从左向右遍历,评分高的孩子多给一颗糖果
再从右向左遍历,评分高的孩子糖果多
'''
class Solution(object):
def candy(self, ratings):
"""
:type ratings: List[int]
:rtype: int
"""
n = len(ratings)
candy_list = [1] * n
for i in range(1,n):
if ratings[i] > ratings[i-1]:
candy_list[i] = candy_list[i-1] + 1
for j in range(n-2,-1,-1):
if ratings[j] > ratings[j+1]:
candy_list[j] = max(candy_list[j], candy_list[j+1]+1)
return sum(candy_list)
ratings = [1,2,2,5,4,3,2]
print(Solution().candy(ratings)) # 14
ratings = [1,0,2]
print(Solution().candy(ratings)) # 5
ratings = [1,2,2]
print(Solution().candy(ratings)) # 412、状态机
12.1、状态机
状态机是一种模型,用来描述对象在其生命周期中的各种状态和状态之间的转换方式。
一个状态机可以被描述为一个初始状态、转移函数、有限状态集的三元组。
在状态机中,对象具有特定的状态,当对象接收到某种事件时,它可以通过执行一系列操作来转移到新的状态。
有限状态机(Finite-state machine, FSM)是有限个状态以及在这些状态之间的转移和动作等行为的数学模型,例如交通信号灯系统。
python中有一个transitions状态机设计库
应用场景:
- 编译器: 编译器可以使用状态机来进行词法分析和语法分析。在编译器中,使用状态机来对输入的代码进行分析,以判断其是否符合语法规则。
- 自动控制系统: 自动控制系统可以使用状态机来实现自动化控制。例如,当温度传感器检测到温度过高时,状态机可以自动控制空调打开,以降低室内温度。
- 人工智能: 在人工智能领域,状态机可以用来描述智能体的行为。智能体根据其当前的状态和输入情况来选择下一步的行动,以实现智能决策
- 游戏编程: 在游戏编程中,状态机可以用来描述游戏对象的行为。例如,在一个动作游戏中,状态机可以用来描述玩家和敌人在攻击、移动、防御等不同的状态之间的转换。
- 自动售货机: 自动售货机可以使用状态机来描述其行为。当顾客选择购买饮料时,自动售货机进入一个等待状态,等待顾客投入硬币。当投入硬币时,状态机进入一个检查状态,检查硬币是否足够。如果硬币足够,状态机进入一个出货状态,出货完成后返回等待状态。
文本解析器: 文本解析器可以使用状态机来处理文本数据。它可以根据当前状态解析文本数据,并在不同状态之间进行转换。例如,在解析HTML文档时,状态机可以通过状态转移来判断标签的开始和结束位置。 - 扫地机器人: 扫地机器人可以使用状态机来描述其行为。当扫地机器人在移动时,它可以根据当前状态进行转移,例如,当它碰到墙壁时,状态机可以将其状态转换为避障状态。
12.2、示例
13.2.1、有效数字
状态图:
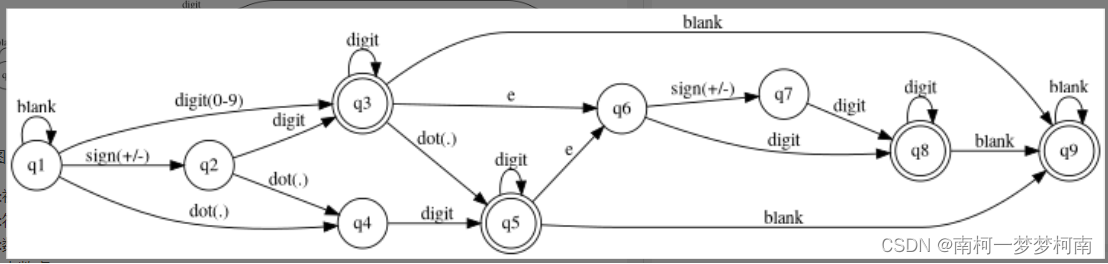
1:初始状态 (空字符串或者纯空格)
2:符号位
3:数字位 (形如-164,可以作为结束)
4:小数点
5:小数点后的数字(形如.721或者-123.6,可以作为结束)
6:指数e
7:指数后面的符号位
8:指数后面的数字(形如+1e-6,可以作为结束)
9:状态3,5,8后面多了空格(主要为了判断"1 1"是不合理的)
python
class Solution:
def isNumber(self, s):
states = [
{}, # 主要为了state和下标对应
# state 1
{"blank":1,"sign":2,"digit":3,"dot":4},
# state 2
{"digit":3,"dot":4},
# state 3
{"digit":3,"dot":5,"e|E":6,"blank":9},
# state 4
{"digit":5},
# state 5
{"digit":5,"e|E":6,"blank":9},
# state 6
{"sign":7,"digit":8},
# state 7
{"digit":8},
# state 8
{"digit":8,"blank":9},
# state 9
{"blank":9}
]
def strToAction(st):
if '0' <= st <= '9':
return "digit"
if st in "+-":
return "sign"
if st in "eE":
return "e|E"
if st == '.':
return "dot"
if st == ' ':
return "blank"
return None
currState = 1
for c in s:
action = strToAction(c)
if action not in states[currState]:
return False
currState = states[currState][action]
return currState in {3,5,8,9}
# 有效的数字
s = ["2", "0089", "-0.1", "+3.14", "4.", "-.9", "2e10", "-90E3", "3e+7", "+6e-1", "53.5e93", "-123.456e789"]
for i in s:
print(Solution().isNumber(i))
print('*'*50)
# 无效的数字
s = ["abc", "1a", "1e", "e3", "99e2.5", "--6", "-+3", "95a54e53"]
for i in s:
print(Solution().isNumber(i))13、链表
13.1、链表
链表是一种在存储单元上非连续、非顺序的存储结构。
数据元素的逻辑顺序是通过链表中的指针链接次序实现。
链表是由一系列的结点组成,结点可以在运行时动态生成。每个结点包含两部分:数据域与指针域。数据域存储数据元素,指针域存储下一结点的指针。
13.1.1、单向链表
单向链表也叫单链表,每个节点包含一个数据元素和指向下一个节点的指针。

python
# 节点类
class Node:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
# 单向链表
class SingleList:
def __init__(self):
self.head = None
def is_empty(self):
return self.head is None
def length(self):
current = self.head
count = 0
while current:
count += 1
current = current.next
return count
def add(self, value):
node = Node(value)
if self.is_empty():
self.head = node
return
node.next = self.head
self.head = node
def append(self, value):
node = Node(value)
if self.is_empty():
self.head = node
return
current = self.head
while current.next is not None:
current = current.next
current.next = node
def insert(self, i, value):
if i < 0 or i > self.length():
raise IndexError
if i == 0:
self.add(value)
return
if i == self.length():
self.append(value)
node = Node(value)
current = self.head
for i in range(i-1):
current = current.next
node.next = current.next
current.next = node
def values(self):
current = self.head
res = []
while current:
res.append(current.val)
current = current.next
return res
def remove(self, value):
# 删除链表中第一个value
current = self.head
pre = None # 当前节点的前一个节点
while current:
if current.val == value:
if pre:
pre.next = current.next
else:
self.head = current.next
break
else:
pre = current
current = current.next
def __str__(self):
return f'len={self.length()} values={self.values()}'
single_list = SingleList()
# 构造一个0-9的链表
for i in range(10):
single_list.append(i)
print(single_list)
single_list.insert(3,3.5) # 在位置3插入3.5
print(single_list)
single_list.remove(3.5) # 删除3.5
print(single_list)
single_list.add(-1)
print(single_list)
'''
len=1 values=[0]
len=2 values=[0, 1]
len=3 values=[0, 1, 2]
len=4 values=[0, 1, 2, 3]
len=5 values=[0, 1, 2, 3, 4]
len=6 values=[0, 1, 2, 3, 4, 5]
len=7 values=[0, 1, 2, 3, 4, 5, 6]
len=8 values=[0, 1, 2, 3, 4, 5, 6, 7]
len=9 values=[0, 1, 2, 3, 4, 5, 6, 7, 8]
len=10 values=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
len=11 values=[0, 1, 2, 3.5, 3, 4, 5, 6, 7, 8, 9]
len=10 values=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
len=11 values=[-1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
''' 13.1.2、双向链表
双向链表也叫双链表,每个节点包含一个数据元素和一个指向上一个节点的指针和一个指向下一个节点的指针。

python
# 节点类
class Node:
def __init__(self, val=0, next=None, prev=None):
self.val = val
self.next = next
self.prev = prev
# 双向链表
class DoublyList:
def __init__(self):
self.head = None
def is_empty(self):
return self.head is None
def length(self):
current = self.head
count = 0
while current:
count += 1
current = current.next
return count
def add(self, value): # 头部插入
node = Node(value)
if self.is_empty():
self.head = node
return
current = self.head
node.next = current
current.prev = node
self.head = node
def append(self, value):
node = Node(value)
if self.is_empty():
self.head = node
return
current = self.head
while current.next is not None:
current = current.next
node.prev = current
current.next = node
def insert(self, i, value):
if i < 0 or i > self.length():
raise IndexError
if i == 0:
self.add(value)
if i == self.length():
self.append(value)
node = Node(value)
current = self.head
for i in range(i-1):
current = current.next
node.next = current.next
node.prev = current
current.next = node
def values(self):
current = self.head
res = []
while current:
res.append(current.val)
current = current.next
return res
def remove(self, value):
# 删除链表中第一个value
current = self.head
while current:
if current.val == value:
if current.prev: # 不是第一个元素
current.prev.next = current.next
else:
self.head = current.next
self.head.pre = None
break
else:
current = current.next
def __str__(self):
return f'len={self.length()} values={self.values()}'
double_list = DoublyList()
for i in range(10):
double_list.append(i)
print(double_list)13.1.3、循环链表
循环链表,每个节点包含一个数据元素和指向下一个节点的指针,最后一个节点的指针指向头节点
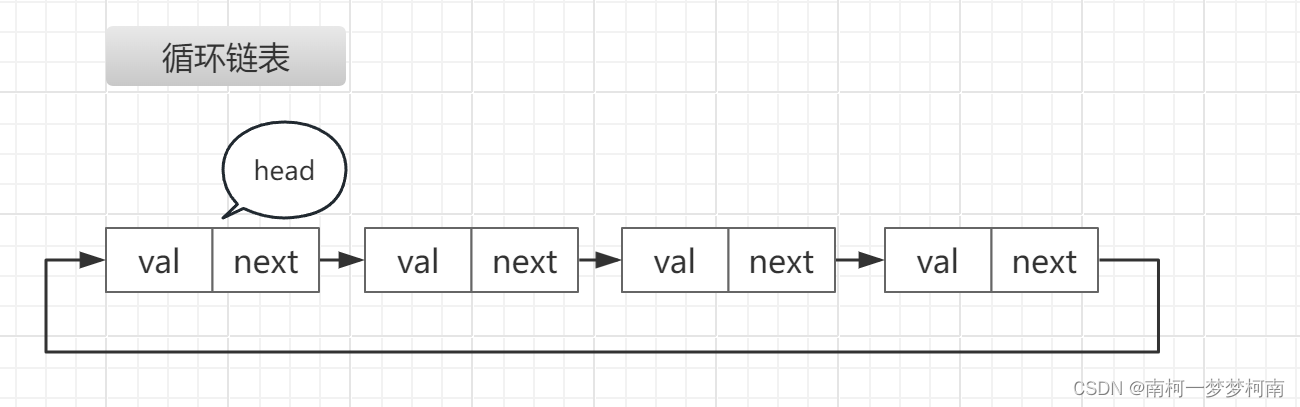
python
# 节点类
class Node:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
# 双向链表
class SingleCycleLinkList:
def __init__(self):
self.head = None
def is_empty(self):
return self.head is None
def length(self):
if self.is_empty():
return 0
current = self.head
count = 1
while current.next != self.head:
count += 1
current = current.next
return count+1
def add(self, value): # 头部插入
node = Node(value)
if self.is_empty(): # 空链表添加,节点指向自己
self.head = node
node.next = self.head
return
node.next = self.head
current = self.head
while current.next != self.head:
current = current.next
current.next = node
self.head = node
def append(self, value):
node = Node(value)
if self.is_empty():
self.head = node
node.next = self.head
return
current = self.head
while current.next != self.head:
current = current.next
current.next = node
node.next = self.head
def insert(self, i, value):
if i < 0 or i > self.length():
raise IndexError
if i == 0:
self.add(value)
if i == self.length():
self.append(value)
node = Node(value)
current = self.head
for i in range(i-1):
current = current.next
node.next = current.next
current.next = node
def values(self):
current = self.head
res = []
while current.next != self.head:
res.append(current.val)
current = current.next
return res
def remove(self, value):
# 删除链表中第一个value
current = self.head
# 第一个元素就是要删除的元素
if current.val == value:
# 链表不止一个元素
if self.length() > 1:
while current.next != self.head:
current = current.next
current.next = self.head.next
self.head = self.head.next
else:
self.head = None
return
# 要删除的元素不是第一个元素
pre = self.head # 记录当前元素的上一个元素
while current.next != self.head:
if current.val == value:
pre.next = current.next
return
else:
pre = current
current = current.next
# 如果删除的是最后一个元素
if current.val == value:
pre.next = self.head
def __str__(self):
return f'len={self.length()} values={self.values()}'
double_list = SingleCycleLinkList()
for i in range(10):
double_list.append(i)
print(double_list)13.2、示例
python
'''
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
head = [1,2,3,4,5], k = 2
res = [4,5,1,2,3]
1、找到最后一个元素和链表长度
2、最后一个元素指向head 链表变成了循环链表
3、找到移动后的head
1 2 3 4 5 6 7 k=1
1 | 2 3 4 5 6 7 分成两部分
2 3 4 5 6 7 1 重新拼接
相当于尾部移动length - k = 6 次
'''
class Solution(object):
def rotateRight(self, head, k):
"""
:type head: ListNode
:type k: int
:rtype: ListNode
"""
if not head or not head.next or k==0:
return head
current = head
length = 1
# 找到最后一个元素 指向head 并记录链表长度
while current.next:
length += 1
current = current.next
current.next = head
# 头部移动k次到目标位置
k = k % length
for _ in range(length-k):
current = current.next
res = current.next
current.next = None
return res14、单调栈
14.1、单调栈
时间复杂度O(n),空间复杂度O(n)
单调栈中存放的数据应该是有序的,所以单调栈也分为单调递增栈 和单调递减栈
- 单调递增栈:比栈顶大的元素出栈,从栈底到栈顶数据是从大到小,如[3,2,1]
- 单调递减栈:比栈顶小的元素出栈,从栈底到栈顶数据是从小到大,如[1,2,3]
单调栈常用来解决两头大小决定中间值的大小的题。
python
# 单调递增栈模板 比栈顶大的元素出栈
def stackIncrease(nums):
stack = []
for num in nums:
while stack and num >= stack[-1]:
stack.pop()
stack.append(num)
return stack
print(stackIncrease([2,1,5,6,2,3])) # [6, 3]
# 单调递减栈模板 比栈顶小的元素出栈
def stackDecrease(nums):
stack = []
for num in nums:
while stack and num <= stack[-1]:
stack.pop()
stack.append(num)
return stack
print(stackDecrease([2,1,5,6,2,3])) # [1, 2, 3]14.2、示例
14.2.1、柱形图中最大的矩形
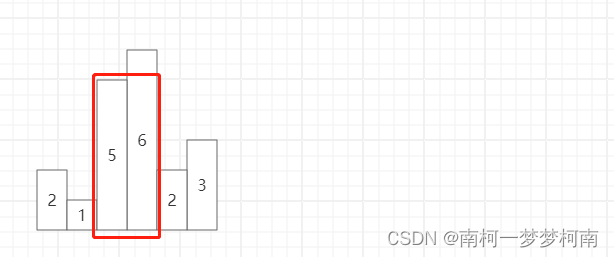
heights=[0,2,1,5,6,2,3,0] # 前后加一个哨兵
找下标i为中心的矩形,
就是找i左边比i低的下标left和i右边比i低的下标right,左右边界取不到,所以宽度为right-left-1
i==1, left=0, right=2
i==2, left=0, right=7
i==3, left=2, right=5
i==4, left=3, right=5
i==5, left=2, right=7
i==6, left=2, right=7
用单调递增栈来记录i左边的比i低的下标left,
如果heights[i] < heights[stack[-1]], 弹出栈顶stack.pop(),并计算面积
stack=[0]
i
1 stack=[0,1]
2 满足条件弹出1, height=heights[1]=2,以下标1为中心,left=0,i=right=2, area=(2-0-1)*2=2, stack=[0,2]
3 stack=[0,2,3]
4 stack=[0,2,3,4]
5 2<=6, 弹出4,height=6, stack=[0,2,3], 以4为中心,left=3, right=5,area=(5-3-1)*6=6
2<=5, 弹出3,height=5,stack=[0,2], 以3为中心,left=2,right=5,area=(5-2-1)*5=10
下一个元素不满足条件,不再弹出,push i ,stack=[0,2,5]
6 stack=[0,2,5,6]
7 0<=3,弹出6,height=3,stack=[0,2,5],以6为中心,left=5,right=7,area=3
0<=2,弹出5,height=2,stack=[0,2],以5为中心,left=2,right=7,area=8
0<=1,弹出2,hegith=1,stack=[0],以2为中心,left=0,right=7,area=6
python
'''
单调栈 单调递减栈 比栈顶小的元素出栈
'''
class Solution:
def largestRectangleArea(self, heights):
heights = [0] + heights + [0] # height前后加一个哨兵
n = len(heights)
stack = [0]
res = 0
for i in range(1,n):
while heights[i] < heights[stack[-1]]:
height = heights[stack.pop()]
area = (i-stack[-1]-1)*height # i是右边界,stack[-1]是左边界,左右边界取不到,再-1
res = max(area, res)
stack.append(i)
return res
print(Solution().largestRectangleArea([2,1,5,6,2,3])) # 10
print(Solution().largestRectangleArea([2,4])) # 4将前i行看作一个柱形图,比如前三行就是
python
class Solution(object):
# 单调栈解法
'''
将前i行看作一个柱形图
把1的格子看成柱子,把0的格子看成空的
'''
def maximalRectangle(self, matrix):
def largestRectangleArea(heights):
heights = [0] + heights + [0] # height前后加一个哨兵
n = len(heights)
stack = [0]
res = 0
for i in range(1,n):
while heights[i] < heights[stack[-1]]:
height = heights[stack.pop()]
area = (i-stack[-1]-1)*height # i是右边界,stack[-1]是左边界,左右边界取不到,再-1
res = max(area, res)
stack.append(i)
return res
m = len(matrix)
n = len(matrix[0])
heights = [0]*n
res = 0
for i in range(m):
for j in range(n):
if matrix[i][j] == '1':
heights[j] += 1
else:
heights[j] = 0
print(heights)
row_max = largestRectangleArea(heights)
res = max(res, row_max)
return res
matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
print(Solution().maximalRectangle(matrix))
'''
[1, 0, 1, 0, 0]
[2, 0, 2, 1, 1]
[3, 1, 3, 2, 2]
[4, 0, 0, 3, 0]
6
'''14.2.2、接雨水
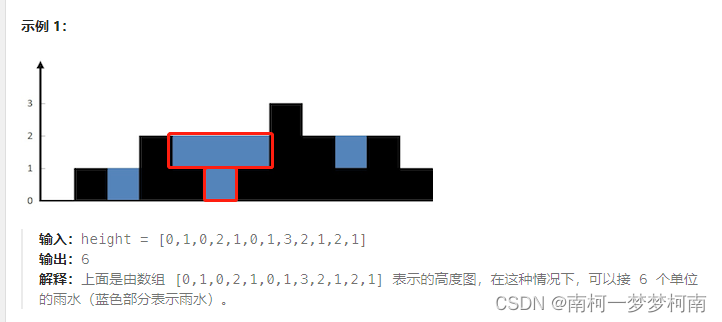
找i位置左右两边比自己高的柱子,计算面积
比如
i=3,left=2,right=6,h=min(height[left],height[right])-height[i],w=right-left-1,area=h*w=3
i=4,left=3,right=5,h=min(height[left],height[right])-height[i],w=right-left-1,area=h*w=1
i=5,left=3,right=6,h=min(height[left],height[right])-height[i],w=right-left-1,area=h*w=0
python
class Solution(object):
# 单调递增栈解法,比栈顶大的元素出栈
def trap(self, height):
n = len(height)
stack = []
res = 0
for i in range(n):
while stack and height[i] > height[stack[-1]]:
index = stack.pop()
if stack:
h = min(height[i], height[stack[-1]])- height[index]
res += h*(i-stack[-1]-1)
stack.append(i)
return res
'''
动态规划解法
从左向右遍历 找i下边对应的左边的最大值
从右向左遍历 找i下标对应的右边的最大值
'''
def trap_dp(self, height):
len_height = len(height)
left_max_list = [0 for _ in range(len_height)]
right_max_list = [0 for _ in range(len_height)]
left_max_list[0] = height[0]
right_max_list[len_height-1] = height[-1]
for i in range(1, len_height):
left_max_list[i] = max(height[i], left_max_list[i-1])
for i in range(len_height-2, -1, -1):
right_max_list[i] = max(height[i], right_max_list[i+1])
res = 0
for i in range(len_height):
res += min(left_max_list[i], right_max_list[i]) - height[i]
return res
height = [0,1,0,2,1,0,1,3,2,1,2,1]
print(Solution().trap(height)) # 6
print(Solution().trap_dp(height))
height = [4,2,0,3,2,5]
print(Solution().trap(height))
print(Solution().trap_dp(height)) # 914.2.3、去除重复字母
python
'''
单调栈
如果字符的字典序小于栈顶元素,且栈顶元素在未遍历序列中还有剩余,就可以出栈
'''
class Solution:
def removeDuplicateLetters(self, s: str) -> str:
stack = []
for index,char in enumerate(s):
if char in stack:
continue
while stack and char < stack[-1] and stack[-1] in s[index:]:
stack.pop()
stack.append(char)
return ''.join(stack)
obj = Solution()
print(obj.removeDuplicateLetters('cbacdcbc')) # acdb
print(obj.removeDuplicateLetters('bcabc')) # abc15、分治法
15.1、分治法
将一个大的问题分解成若干个小的问题,并且这些小问题与大问题的问题性质保持一致,通过处理小问题从而处理大问题。这里用到了递归的思想。
分治法思想:
- 分:将整个问题分成多个子问题。
- 求解:求解各个子问题。
- 合并:合并所有子问题的解,从而得到原始问题的解。
在使用分治法设计算法的时候,最好使得各个子问题之间相互独立,如果各个子问题不是独立的,那么分治法会求一些重复求解的重叠子问题,这会导致做很多重复工作,使得算法的效率下降,此时使用动态规划算法更好。
排序算法中的归并排序和快速排序就是使用的分治法思想
分治法常用来解决以下问题:
- 组合问题中的最大子段和问题
- 几何问题中的最近点对问题
- 棋盘覆盖问题
- 二分查找
- 等等
15.2、示例
16、数学公式
16.1、笛卡尔积
笛卡尔积(Cartesian product):笛卡尔乘积是指在数学中,两个集合X和Y的笛卡尔积,又称直积,表示为X × Y,第一个对象是X的成员而第二个对象是Y的所有可能有序对的其中一个成员。
python
'''
集合A={a,b}, B={0,1,2},笛卡尔积结果为:
A×B={(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}
B×A={(0, a), (0, b), (1, a), (1, b), (2, a), (2, b)}
python默认迭代器库itertools提供笛卡尔积计算函数product
'''
import itertools
A = ['a','b']
B = [0,1,2]
c = itertools.product(A, B) # itertools.product是一个迭代器
print(c) # <itertools.product object>
print(list(c)) # [('a', 0), ('a', 1), ('a', 2), ('b', 0), ('b', 1), ('b', 2)]
# permutations:排列
print(list(itertools.permutations(B, 2))) # [(0, 1), (0, 2), (1, 0), (1, 2), (2, 0), (2, 1)]
print(list(itertools.permutations(B, 3))) # [(0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1), (2, 1, 0)]
# combinations:组合
print(list(itertools.combinations(B, 2))) # [(0, 1), (0, 2), (1, 2)]
print(list(itertools.combinations(B, 3))) # [(0, 1, 2)]