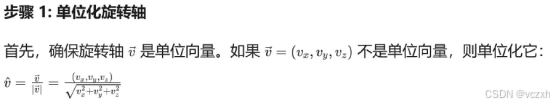平移矩阵、点绕轴的旋转矩阵、平面直角坐标系旋转矩阵、点绕向量旋转公式(罗德里格斯旋转公式)

平移矩阵

点绕轴的旋转矩阵

平面直角坐标系旋转矩阵

点绕向量旋转公式(罗德里格斯旋转公式)

代码

#include "myPoint.h"
#include <cmath>
myPoint::myPoint()
{
	m_x = m_y = m_z = 0;
}

myPoint::myPoint(double x, double y, double z):m_x(x),m_y(y),m_z(z)
{
}

myPoint::myPoint(const myPoint& ref) : m_x(ref.X()), m_y(ref.Y()), m_z(ref.Z())
{
}

myPoint myPoint::operator=(const myPoint& rhs)
{
	SetX(rhs.X());
	SetY(rhs.Y());
	SetZ(rhs.Z());
	return *this;
}

void myPoint::SetX(double x)
{
	m_x = x;
}

void myPoint::SetY(double y)
{
	m_y = y;
}

void myPoint::SetZ(double z)
{
	m_z = z;
}

double myPoint::X()const
{
	return m_x;
}

double myPoint::Y()const
{
	return m_y;
}

double myPoint::Z()const
{
	return m_z;
}

myPoint myPoint::add(myPoint& rhs)const
{
	myPoint ret(0.0, 0.0, 0.0);
	ret.SetX(m_x + rhs.X());
	ret.SetY(m_y + rhs.Y());
	ret.SetZ(m_z + rhs.Z());
	return ret;
}

myPoint myPoint::Sub(myPoint& rhs)const
{
	myPoint ret(0.0, 0.0, 0.0);
	ret.SetX(m_x - rhs.X());
	ret.SetY(m_y - rhs.Y());
	ret.SetZ(m_z - rhs.Z());
	return ret;
}

myPoint myPoint::cross(myPoint& rhs)const
{
	myPoint ret(0.0, 0.0, 0.0);
	ret.SetX(m_y * rhs.Z() - m_z * rhs.Y());
	ret.SetY(m_z * rhs.X() - m_x * rhs.Z());
	ret.SetZ(m_x * rhs.Y() - m_y * rhs.X());
	return ret;
}

myPoint myPoint::Normalize() const
{
	myPoint ret(0.0, 0.0, 0.0);
	ret.SetX(m_x / Length());
	ret.SetY(m_y / Length());
	ret.SetZ(m_z / Length());
	return ret;
}

double myPoint::Length() const
{
	return sqrt(m_x * m_x + m_y * m_y + m_z * m_z);
}

myPoint myPoint::Scale(const double& rhs) const
{
	myPoint ret(0.0, 0.0, 0.0);
	ret.SetX(m_x * rhs);
	ret.SetY(m_y * rhs);
	ret.SetZ(m_z * rhs);
	return ret;
}

double myPoint::Dot(const myPoint& rhs) const
{
	return m_x * rhs.X() + m_y * rhs.Y() + m_z * rhs.Z();
}

myPoint myPoint::Reversal() const
{
	return myPoint(-X(), -Y(), -Z());
}


#include "myMatrix4x4.h"
#include <cmath>
myMatrix4x4::myMatrix4x4()
{
	Identity();
}

void myMatrix4x4::Zero()
{
	for (int i = 0; i < 4; ++i)
	{
		for (int j = 0; j < 4; ++j)
		{
			m_Element[i][j] = 0;
		}
	}
}

void myMatrix4x4::Identity()
{
	for (int i = 0; i < 4; ++i)
	{
		for (int j = 0; j < 4; ++j)
		{
			if (i == j)
			{
				m_Element[i][j] = 1.0;
			}
			else
			{
				m_Element[i][j] = 0.0;
			}
		}
	}
}

void myMatrix4x4::SetElement(int i, int j, double value)
{
	m_Element[i][j] = value;
}

void myMatrix4x4::Move(const myPoint& vec)
{
	Identity();
	SetElement(0, 3, vec.X());
	SetElement(1, 3, vec.Y());
	SetElement(2, 3, vec.Z());
}
//绕vec向量旋转radian度的矩阵
void myMatrix4x4::Rotate(const myPoint& vec, const double& radian)
{
	Identity();
	float dx = vec.X() / vec.Length();
	float dY = vec.Y() / vec.Length();
	float dZ = vec.Z() / vec.Length();

	SetElement(0, 0, cos(radian) + (dx * dx) * (1 - cos(radian)));
	SetElement(1, 0, dx * dY * (1 - cos(radian)) - dZ * sin(radian));
	SetElement(2, 0, dx * dZ * (1 - cos(radian)) + dY * sin(radian));
	SetElement(0, 1, dx * dY * (1 - cos(radian)) + dZ * sin(radian));
	SetElement(1, 1, cos(radian) + dY * dY * (1 - cos(radian)));
	SetElement(2, 1, dY * dZ * (1 - cos(radian)) - dx * sin(radian));
	SetElement(0, 2, dx * dZ * (1 - cos(radian)) - dY * sin(radian));
	SetElement(1, 2, dZ * dY * (1 - cos(radian)) + dx * sin(radian));
	SetElement(2, 2, cos(radian) + dZ * dZ * (1 - cos(radian)));
}
//点按this矩阵运算返回运算结果
myPoint myMatrix4x4::MultiplyPoint(const myPoint& pt)const
{
	myPoint retPt;
	double v0 = pt.X();
	double v1 = pt.Y();
	double v2 = pt.Z();
	double v3 = 1;
	double ret[4];
	for (int i=0;i<4;i++)
	{
		ret[i] = m_Element[i][0] * v0 + m_Element[i][1] * v1 + m_Element[i][2] * v2 + m_Element[i][3] * v3;
	}
	retPt.SetX(ret[0]);
	retPt.SetY(ret[1]);
	retPt.SetZ(ret[2]);
	return retPt;
}