前面我们学习了确定型、单周期以及其他类型的随机型存储模型,相信大家对存储论的相关知识已经有了一定的了解,本期小编将带大家学习存储论在应用研究中的一些问题。
库存管理的实际需求是非常迫切的,即使是简单的库存策略,也会带来巨大的经济效益。运筹学的任务是建立更实用的库存模型,并用于实际。下面我们一起来了解三种存储论的实际应用情景。
1.多品种多级库存系统的控制
多品种多级库存系统可以用下图表示。
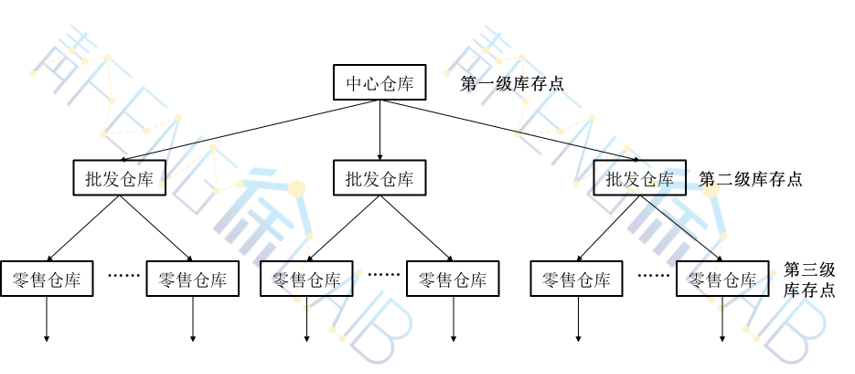
图中,最高的第一级是货源点(中心仓库),它供应第二级的库存点。最低一级的库存点(如零售仓库)直接满足顾客的需求。而货源点直接从外界订货(或组织生产)。
多品种多级库存系统的一个特点是可能有多种不同的订货策略:
(1)单个物品分别订货;
(2)联合订货,即同时订购所有物品;
(3)混合式策略,指允许同时订购所有的物品或部分物品。
对于这三种订货策略,每次订货的固定费用对最优策略有显著影响,以n 种货物为例,一次单独订购货物的固定费用为Ki ,联合订购时为K,一般有
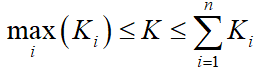
问题复杂性表现在以下几个方面:
(1)系统的层次结构使库存策略的需求过程是一个复杂的叠加;
(2)决策变量需要从系统的角度同时优化;
(3)某一级的安全库存量会影响另一级的情况,多级问题需从总体上考虑;
(4)出现缺货时,可采用的处理方式灵活多样;
(5)不论采用动态规划、启发式计算等方法的计算量都非常大;
(6)管理多级系统需要协调各项活动,局部利益常妨碍系统成功实施。
目前,存储论领域已经开发出一些比较实用的库存控制方法,例如发送式库存(PUSH)系统。发送式库存系统采取集中控制,从系统全局着眼把货物发送到下一级,这样可以消除过多的订货次数,使费用减小并达到要求的服务水平。
**2.易腐物品库存管理
在库存问题的研究中,通常假定存放物品的使用价值保持不变,即假定物品的寿命等于无穷。但许多实际情况并非如此,如血库中供输血用的血液一般可存放21天,其寿命为常数。还有一些物品,如农产品、食品、药品、武器弹药等,其寿命无法事先确定,因而通常作为非负随机变量来处理。
由于这种实际的需要,近年来对易腐物品库存管理开展了不少研究。例如,航空公司及酒店管理中的收益管理就与易腐物品的库存管理性质相同:
**(1)"寿命"有限。**航空公司和酒店的座位或房间是一种类似易腐物品的资源。在某个特定时间点(如航班起飞或当晚住宿)之后就会"过期",即失去其销售价值。
**(2)收益管理策略。**航空公司和酒店通常使用动态定价、预订控制和库存管理等策略来实现最大化收益。这与易腐物品库存管理中的策略类似,比如对库存进行动态调整、定价策略的优化等。
易腐物品库存模型按存货寿命,分为固定寿命和随机寿命两类。
如,固定寿命m下的模型假定:
(1)周期盘点。周期开始订货、瞬时交货,新到货年龄为0;
(2)相继周期的需求量独立同分布,且分布已知,不能满足的需求事后补足;
(3)先进先出规则。当某部分存货年龄超过m时,该部分货物报废;
(4)费用:包括购货费、保管费、缺货损失费及过期损失费。
由于易腐物品库存模型(特别是随机寿命类型)的复杂性,寻找最优策略是十分困难的。**现有的研究主要集中在各种限定条件下的近似最优策略上。**例如:
(1)当库存量小于某个规定的临界值才订货,否则不订货的情形;
(2)在周期盘点下保持库存量为常数的情形;
(3)当库存物品由于需求或过期而减少一个时就订货,且只订一个的情形;
(4)易腐物品库存模型中考虑不耐烦顾客排队系统理论的研究,比如客户需求波动、交货延迟、或由于库存管理策略不当而导致客户等待时间过长,进而放弃购买的情况。
这些研究都有很鲜明的实际背景。
**3.概率约束的库存管理
问题一般描述为:设工厂B以固定速度消耗某种原材料。季度开始之前,B与A签订合同,由A提供该季度B需要的原材料。A可分若干次交货,但不确定具体交货时间。为保障生产连续进行,B在季度开始时需要一定量的原材料储备。那么应储备多少才能维持正常生产?
把问题抽象成这样的基本模型:
考虑在固定区间(0,T )内,假定交货次数n一定,设:
(1)B工厂在(0,T )中连续使用这些原材料,单位时间用量为c(常数);
(2)交货时刻随机,为(0,T )内独立同分布的n个均匀随机变量;
(3)每次的交货量相同,为
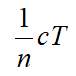
取B初始库存水平M 为模型决策变量。记X(t) 为时刻t 以前的累积交货量,则求下式的M:
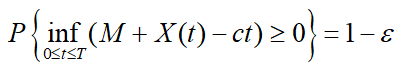
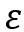
为事先指定的(0,1)中的数。
上述基本模型有许多推广。例如,每次交货量相等的条件可减弱;B工厂以均匀速率消费原材料的过程可推广到更一般的随机过程;此外,还可推广到多种原材料的模型等。
以上就是本期存储论的一些实际应用的全部内容啦,通过对这一期的学习,相信大家一定能够加深对存储论的理解,进而在生活实践中学会应用!